Uma escada homogênea com de comprimento e de peso está apoiada em uma parede vertical sem atrito. O coeficiente de atrito estático entre o chão e o pé da escada é . Qual é a maior distância a que o pé da escada pode estar da base da parede sem que a escada escorregue?
Passo 1
Vamos começar desenhando a situação:
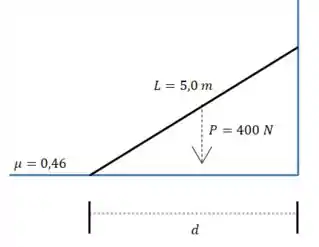
A questão quer saber o seguinte: até onde podemos aumentar sem que a escada escorregue? Isso é o mesmo que perguntar: qual o máximo valor de que não impede o equilíbrio do sistema?
A dica está aí: temos que usar as equações do equilíbrio: a soma dos torques tem que ser nula, e a soma das forças tem que ser nula.
Passo 2
Vamos começar usando o equilíbrio das forças. Vamos dar nome às forças e aos ângulos envolvidos.
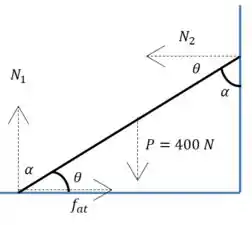
O equilíbrio tem que acontecer em todas as direções. Vamos começar pelas forças horizontais, escolhendo um dos sentidos como sendo positivo:
E as forças verticais, também escolhendo um dos sentidos como positivo:
E daí temos:
Vamos dividir uma equação do sistema pela outra, pra ficarmos com uma igualdade só:
Mas como , podemos adicionar mais um termo na igualdade!
Beleza. Agora vamos para o equilíbrio dos torques.
Passo 3
Para calcular os torques, precisamos colocar um referencial em algum lugar. Uma dica: é sempre bom colocar o referencial em cima de um ponto que não queremos calcular E que não conhecemos.
Nesse caso, não conhecemos as forças em nenhuma das pontas da escada, mas seria bom achar o valor de pra substituir na equação de cima. Então vamos colocar o pé em cima de .
Obs.: Lembre que é preciso multiplicar pelos senos dos ângulos que as forças fazem com a escada!
Agora, olhando para os diagramas acima, veja o seguinte:
Onde é a altura com que a escada toca a parede, e é a distância entre a parede e o pé da escada.
Ou seja:
Passo 4
Agora vamos ver o que nós temos. Pelo equilíbrio das forças achamos:
E pelo equilíbrio dos torques achamos:
Substituindo uma na outra pra achar :
Agora isolando :
E o único problema agora é achar , mas pelo teorema de Pitágoras:
E substituindo na fórmula, fica:
Agora vamos isolar :
Agora substituindo os valores:
Pronto!
Resposta
A distância máxima é