Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.2 - Ex. 14
No experimento de difração de fenda única da Fig. 36-4, suponha que o comprimento de onda da luz é 500 nm, a largura da fenda é e a tela de observação está a uma distância . Defina o eixo como um eixo vertical no plano da tela, com a origem no centro da figura de difração. Chame de a intensidade da luz difratada no ponto , situado em . (a) Qual é a razão entre e a intensidade no centro da figura de difração? (b) Determine a posição do ponto na figura de difração especificando o máximo e mínimo entre os quais o ponto se encontra ou os dois mínimos entre os quais o ponto se encontra.
Passo 1
Nesse exercício vamos usar uma relação trigonométrica para descobrir qual o ângulo do ponto P como também usar as relações para 36-6 e 36-5 para calcularmos a intensidade no mesmo ponto.
Passo 2
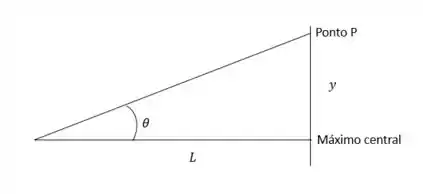
- A situação descrita pelo enunciado é da forma mostrada na imagem acima (confia). Dessa forma, podemos descobrir o ângulo através do valor de sua tangente. Assim, temos que
- Se considerarmos o ponto como um possível ponto de “mínimo”, podemos utilizar a Eq. 36-3 para determinar qual seu valor de e descobrir onde o mesmo se localiza, uma vez que temos seu ângulo . Assim, a equação será dada por
Calculando agora o através da equação 36-6, temos que
Substituindo os valores dados pelo problema, temos que
Agora usando a relação 36-5, podemos calcular a razão entre as intensidades através da equação
Passo 3
Assim, temos que o ponto está localizado entre o máximo central e o primeiro mínimo de difração.