Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 14.4 - Ex. 24
Na Fig. 14-35, a água atinge uma altura atrás da face vertical de uma represa com de largura. Determine (a} a força horizontal a que está submetida a represa por causa da pressão manométrica da água e (b) o torque produzido por essa força em relação a uma reta que passa por O e é paralela à face plana da represa. Determine o braço de alavanca desse torque.
Passo 1
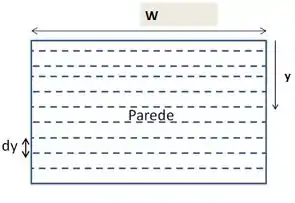
- De acordo com o resultado demonstrado no problema 19 dessa mesma seção, a força produzida por um fluido sobre uma parede vertical de um recipiente que o contém é dada pela integral das infinitas forças que variam com em cada ponto ao longo da altura do líquido.
- Aqui, precisamos lembrar do conceito de Torque. Lembre-se que ele é obtido pelo produto entre o módulo de uma força e o seu “braço”, ou seja, a distância entre sua linha de ação e o ponto considerado. Nesse caso, como a força varia com a altura (como já vimos no problema 19), o torque também varia. Cada pequena força de módulo exerce um torque igual a
Lembra do raciocínio que utilizamos? Para obtê-la, nós fizemos o somatório das infinitas forças de módulo
Daí, obtivemos:
Sendo a distância do ponto considerado até a superfície do fluido. Nesse caso, temos:
Realizando a integral acima, temos como resultado
ou seja:
Passo 2
tomando como referência o ponto O indicado na Figura.
Passo 2
Assim como na questão 19, temos aqui a mesma situação de somatório infinito de quantidades bem pequenas que variam com (representadas por ). Nesse caso, para obter o somatório dessas quantidades, realizamos a seguinte integral
Passo 3
Integrando de 0 a D, obtemos:
Passo 4
(c ) Para obtermos o braço de alavanca desse torque, utilizamos o conceito de momento que comentamos na letra (b): . Considerando como igual ao braço pedido, temos:
Sendo e a força e o torque calculados anteriormente. Logo, vem:
Isolando r: