Exercícios de Pressão Hidrostática - Lista de Exercícios Resolvida
Questão 1
Alguns membros da tripulação tentam escapar de um submarino avariado abaixo da superfície. Que força deve ser aplicada a uma escotilha de emergência, de por ,
para abri-la para fora nessa profundidade? Suponha que a massa específica da água do oceano é e que a pressão do ar no interior do submarino é .
Ver solução completaQuestão 2
Os cientistas encontraram indícios de que Marte pode ter tido outrora um oceano com de profundidade. A aceleração da gravidade em Marte é .
- Qual seria a pressão manométrica no fundo desse oceano?
- A que profundidade você precisaria descer nos oceanos da Terra para ser submetido à mesma pressão manométrica?
Dados necessários:
Densidade da água do mar: .
Aceleração da gravidade na Terra: .
Ver solução completaQuestão 3
A profundidade máxima a que um mergulhador pode descer com um snorkel (tubo de respiração) é determinada pela massa específica da água e pelo fato de que os pulmões humanos não funcionam com uma diferença de pressão (entre o interior e o exterior da cavidade torácica) maior que . Qual é a diferença entre os valores de , para água doce e para a água do mar Morto (a água natural mais salgada no mundo com uma massa específica de )?
Dados:
Ver solução completaQuestão 4
A figura mostra três vasos , e cujas bases tem a mesma área. Os vasos estão cheios de líquido , e até uma mesma altura. As pressões nos fundos dos vasos são , e , respectivamente. Com relação a essa situação, é correto afirmar que:
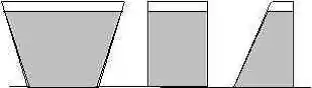
- somente se os líquidos , e forem idênticos.
- quaisquer que sejam os líquidos , e .
- somente se os líquidos , e forem idênticos.
- quaisquer que sejam os líquidos , e .
Questão 5
Um barril contém uma camada de óleo de flutuando sobre água. A camada de água tem uma altura de . A densidade do óleo é igual a .
- Qual é a pressão manométrica na interface entre o óleo e a água?
- Qual é a pressão manométrica no fundo do barril?
Outros dados:
Ver solução completaQuestão 6
Você está projetando um sino de mergulho pra aguentar a pressão da água do mar até uma profundidade de
a) Qual é a pressão manométrica nessa profundidade? (Despreze as variações de densidade da água com a profundidade).
b) Levando-se em consideração a pressão da coluna de líquido e a pressão atmosférica, qual é a força resultante exercida pela água fora do sino e pelo ar dentro do sino sobre uma janela de vidro circular com diâmetro de ? (Despreze a pequena variação de pressão sobre a superfície da janela).
Dados necessários:
Ver solução completaQuestão 7
Um cilindro alto com uma área de seção reta igual a está parcialmente cheio de mercúrio. A superfície do mercúrio está acima do fundo do cilindro. Despeja-se água lentamente sobre o mercúrio, e os dois fluidos não se misturam. Que volume de água deve ser acrescentado para dobrar a pressão manométrica no fundo do cilindro?
Dados:
Ver solução completaQuestão 8
Embolia gasosa em viagens de avião. Os mergulhadores são aconselhdados a não viajar de avião nas primeiras 24h após um mergulho porque o ar pressurizado usado durante o mergulho pode introduzir nitrogênio na corrente sanguínea. Uma redução súbita da pressão do ar (como a que acontece quando um avião decola) pode fazer com que o nitrogênio forme bolhas no sangue, que podem produzir embolias dolorosas ou mesmo fatais. Qual é a variação de pressão experimentada por um soldado da divisão de operações especiais que mergulha a de profundidade em um dia e salta de paraquedas de uma altitude de no dia seguinte? Suponha que a massa específica média do ar nessa faixa de altitude é .
Dados:
Ver solução completaQuestão 9
A densidade de massa da atmosfera decresce com a altura a partir do nível do mar. A pressão e a densidade de massa da atmosfera no nível do mar são dadas por e , respectivamente. Considere que a aceleração da gravidade é constante e conhecida. Supondo que a temperatura é constante e a atmosfera pode ser considerada um gás ideal, a pressão na altura é dada por , onde é
Questão 10
A densidade de um corpo é ligeiramente menor do que a da água. No entanto, ele é muito mais compressível. O que acontecerá se ele for colocado próximo à superfície e se for colocado a uma grande profundidade, respectivamente?
- Ele afundará no primeiro e no segundo
- Ele boiará na superfície no primeiro caso e no segundo
- Ele boiará na superfície no primeiro caso e afundará no segundo
- Ele afundará no primeiro caso e boiará no segundo
- Ele boiará na superfície no primeiro caso e no segundo, mas com uma fração maior fora d’água no segundo caso
Questão 11
Os três paralelepípedos abaixo tem a mesma altura e a mesma área da base .
Nos três casos, o ponto está em contato com a base e com uma superfície lateral.
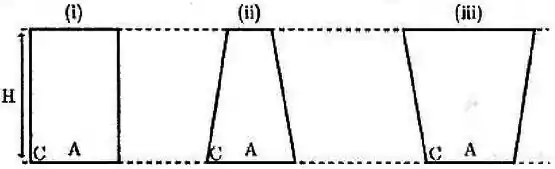
Se os três estiverem completamente preenchidos pelo mesmo fluido, marque a alternativa verdadeira:
- A pressão do fluido sobre a superfície lateral, no ponto , é maior no caso .
- A pressão do fluido sobre a superfície lateral, no ponto , é maior no caso .
- A pressão do fluido sobre a superfície lateral, no ponto , é maior no caso .
- O fluido exerce pressão sobre a superfície lateral apenas no caso .
- A pressão do fluido sobre a superfície lateral, no ponto , é igual em todos os casos.
Questão 12
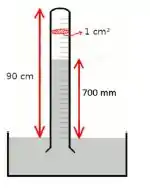
A figura mostra um tubo de vidro do barômetro de mercúrio cujo espaço acima da superfície livre do reservatório de mercúrio tem um volume de . Num dia em que a temperatura ambiente é de 20°C e a pressão atmosférica verdadeira é de 750 mmHg, a altura da coluna barométrica é de 700 mmHg. Calcule o número de mols de ar aprisionado no espaço acima da coluna de mercúrio.
Questão 13
A uma certa profundidade no oceano, a pressão absoluta é p. Se você for ao dobro dessa profundidade (tratando a água como incompressível):
A) a pressão absoluta será 2p.
B) a pressão absoluta será menor que 2p.
C) a pressão absoluta será maior que 2p.
D) a pressão manométrica não será alterada.
E) a pressão manométrica aumentará, mas não dobrará.
Ver solução completaQuestão 14
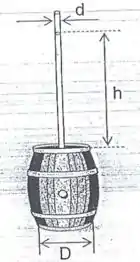
Quando apresentou o seu princípio, Pascal fez uma demonstração dramática. Ele inseriu um tubo fino de diâmetro verticalmente num barril fechado como mostra a figura abaixo. A tampa do barril tem um diâmetro Depois de preencher o barril com água, ele continuou preenchendo o tubo com água. Quando a altura da coluna de água no tubo atingiu a altura , o barril explodiu. Em um instante imediatamente anterior a explosão, calcule o que se pede.
Se necessário use , a densidade da água e
- O peso da água no tubo.
- A pressão manométrica da água logo abaixo da tampa do barril
- A força líquida(módulo, direção e sentido) na tampa do barril.
Questão 15
Um tanque contém uma camada de mercúrio de 0,30 m de profundida coberta por uma camada de água com 1,2 m de profundida. A densidade da água é kg/m³ e do mercúrio é kg/m³. Qual é a pressão exercida pela dupla camada de líquidos na base do tanque? Despreza a pressão atmosférica.
Ver solução completaQuestão 16
2 - A figura abaixo mostra um recipiente cheio de água até a altura mostrada. Quando comparamos a pressão no ponto A com a pressão no ponto B, descobrimos que
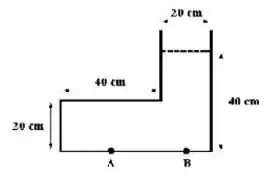
Questão 17
O tanque fechado mostrado na figura é preenchido com água e tem de profundidade. Um manômetro, conectado a tampa do tanque, registra o valor de . Determine:
- A altura da coluna de água no tubo conectado ao tanque para que o fluido permaneça em repouso, considerando a extremidade superior do tubo aberta
- A pressão manométrica atuando no fundo do tanque
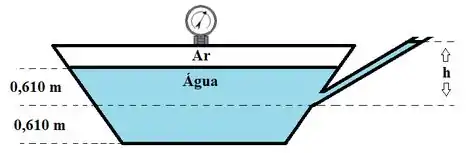
Questão 18
Um barômetro de mercúrio marca ao nível do mar. Quando ele é levado para uma altitude de , a altura da coluna de mercúrio passa a ser a metade, . Admita que a atmosfera é aproximadamente isotérmica, de forma que a pressão é proporcional a densidade do ar . Se o mesmo barômetro for levado até uma altitude de , a altura da coluna de mercúrio passará a ser
Questão 19
Uma piscina com de largura e de comprimento está cheia até a borda. Se a força total que a água exerce sobre o fundo da piscina é , qual é a pressão da água no fundo da piscina?
Questão 20
Durante a atividade de exploração de petróleo, principalmente quando ocorre em águas profundas, é necessário operar em profundidades em torno de 150 m. Muitas vezes quem realiza esse trabalho são os mergulhadores que utilizam roupas especiais capazes de aguentar a pressão da coluna de água. Qual deve ser a intensidade da força por de área, que essa roupa especial suporta essa profundidade?
Questão 21
Quando a pressão atmosférica aumenta uma certa quantidade, o que acontece com a pressão absoluta no fundo de uma piscina?
A) não muda
B) aumenta em menor quantidade
C) aumenta na mesma quantidade
D) aumenta em maior quantidade
E) depende da profundidade da piscina
Ver solução completaQuestão 22
Uma pessoa mede a pressão absoluta à profundidade de em um container com um líquido desconhecido e encontra . ()
Qual é a massa específica desse líquido?
Ver solução completaQuestão 23
(Cap 14 - Ex 30) Uma esfera de plástico oca é mantida submersa em um lago de água doce amarrada a uma corda presa no fundo do lado. O volume da esfera é igual a , e a tensão na corda é igual a 900N. a) calculce a força de empuxo exercida pela água sobre a esfera. B) qual é a massa da esfera? c) a corda se rompe e a esfera sobe até a superfície. Quando ela atinge o equilíbrio, qual é a fração do volume da esfera que fica submersa?
Ver solução completaQuestão 24
Na figura dada, três recipientes de mesma altura e área de base estão totalmente preenchidos com água. Sendo , , e os módulos da força de contato em cada base de apoio, do peso do líquido e a força de pressão do líquido no fundo do recipiente, indique quais das afirmações abaixo são corretas:
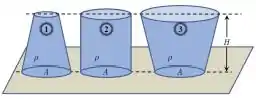
Escolha uma:
- (1),(2) e (4)
- (3) e (4)
- (3)
- (2) e (5)
- Todas as afirmações.
Questão 25
(Cap 14 - Ex 27) Uma amostra de minério pesa 17,50N no ar. Quando a amostra é suspensa por uma corda leve e totalmente imersa na água, a tensão na corda é igual a 11,20N. Calcula o volume total e a densidade da atmosfera.
Ver solução completaQuestão 26
(Cap 14 - Ex 31) Um bloco de madeira cúbico com aresta de 10,0 cm flutua sobre uma interface entre uma camda de água e uma camada de óleo, com uma base situada 1,50 cm abaixo da superfície livre do óleo (Figura 14.34). A densidade do óleo é igual a . a) Qual é a pressão manométrca na face superior do bloco? b) Qual é a pressão manométrica na face interior do bloco? c) Quais são a massa e a densidade do bloco?
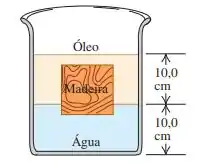
Questão 27
A figura abaixo mostra três recipientes com a mesma área da base e contendo o mesmo fluido incompressível, que exerce a mesma força F sobre a base. Considere que os recipientes têm a mesma massa.
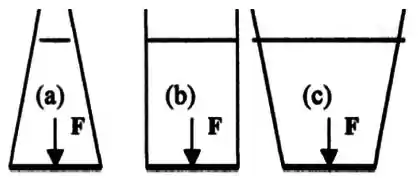
De acordo com o paradoxo hidrostático, podemos dizer que, a relação correta entre a força e o peso de fluido em cada um dos recipientes é:
Ver solução completa
Questão 28
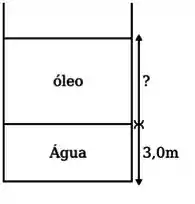
Na figura, um tanque aberto contém uma camada de óleo que flutua no topo de uma camada de água (densidade de ), que é de de espessura, como mostrado. Qual deve ser a espessura da camada de óleo se a pressão manométrica no fundo do tanque é de ? A densidade do óleo é de .
Ver solução completa
Questão 29
A figura mostra o gráfico da pressão manométrica em função da profundidade para três fluidos em equilíbrio no campo gravitacional, suposto constante. Considere as seguintes afirmações:
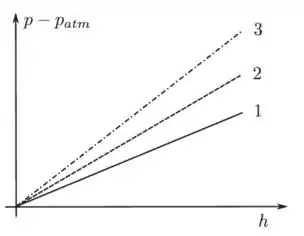
I. O empuxo sobre um mesmo corpo totalmente submerso é maior para o fluido 1.
II. Os três fluidos são incompressíveis.
III. Se colocarmos uma mesma massa M de cada fluido em recipientes idênticos, separados, a altura de fluido será a mesma em todos.
Marque a opção CORRETA.
(a) Somente a I está correta.
(b) Somente a II está correta.
(c) Somente a III está correta.
(d) Somente I e II estão corretas.
(e) Somente II e III estão corretas.
(f) Somente I e III estão corretas.
(g) Todas estão corretas.
(h) Nenhuma está correta.
Ver solução completaQuestão 30
Um balde em repouso no chão de um elevador contém um fluido incompressível de densidade ρ. Quando o elevador desce com aceleração constante de magnitude , a diferença de pressão entre dois pontos de um fluido, separados por uma distância vertical , é dada por:
Ver solução completaQuestão 31
Um balde em repouso no chão de um elevador contém um fluido incompressível de densidade ρ. Quando o elevador tem uma aceleração para baixo de magnitude , a diferença de pressão entre dois pontos quaisquer no fluido, separados por uma distância vertical ∆h, será:
Nenhuma das respostas é verdadeira.
Ver solução completaQuestão 32
Um recipiente próximo a superfície terrestre onde a aceleração da gravidade é , com g constante, e contendo um fluido de densidade constante e massa é submetido a uma força adicional, uniforme, , onde A e B são constantes positivas.
Como varia a pressão no interior do fluido, considerando que o mesmo se encontra em equilíbrio?
(a)
(b)
(c)
(d)
(e)
(f)
(g) Nenhuma das respostas anteriores.
Ver solução completa