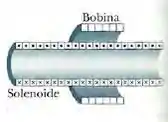
Na figura 30-39, uma bobina de espiras, com de raio e uma resistência de , é coaxial com um solenoide de e de diâmetro. A corrente no solenoide diminui de para zero em um intervalo de tempo . Qual é a corrente induzida na bobina no intervalo ?
Passo 1
E aí! tudo certinho? 😬

Nesse problema temos uma bobina de espiras, com de raio e uma resistência de , é coaxial com um solenoide de e de diâmetro. A corrente no solenoide diminui de para zero em um intervalo de tempo . A partir daí queremos saber qual é a corrente induzida na bobina no intervalo .
Tem ideia de como fazemos isso? 🤔
Bom, galera, um cara chamado Faraday descobriu que uma força eletromotriz e uma corrente podem ser induzidas em uma espira fazendo variar a quantidade de campo magnético que atravessa a espira. Ele ainda percebeu que a dita “quantidade de campo magnético” pode ser visualizada em termos das linhas de campo magnético que atravessam a espira.
O número de linhas que atravessam a espira não importa; os valores da força eletromotriz e da corrente induzida são determinados pela taxa de variação desse número. O módulo da força eletromotriz induzida em uam espira condutora é igual à taxa de variação com o tempo do fluxo magnético que atravessa a espira. A expressão para caluclar a força eletromotriz é a seguinte:
O sinal negativo mostra que a força eletromotriz se opõe à variação do fluxo.
Veja só! 😁
Passo 2
Se por algum acaso o fluxo através de uma bobina de espiras sofre uma variação, uam força eletromotriz é induzida em cada espira ea força eletromotriz total é a soma dessas forças eletromotrizes. Se as espiras da bobina estão muito próximas (como se fosse um enrolamento compacto), o mesmo fluxo magnético atravessa todas as espiras e a força eletromotriz total induzida na bobina é dada por:
Assim, na nossa questão queremos calcular corrente induzida na bobina que tem várias espiras. Esse caso se assemelha com o descrito acima, on . Então, vamos usar a lei de Faraday para calcular primeiro a força eletromotriz e depois vamos usar a lei de Ohm para achar a tão requisita corrente..
Substituindo os valores na expressão, temos:
Tranuilo até aqui? 😬
Passo 3
Para calcular agora a corrente vamos aplicar a lei de Ohm!
E aí! entendeu tudo? Responde Aí! 😉

Resposta
A corrente induzida é igual a: