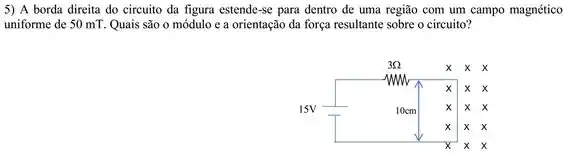
Exercícios de Lei de Lenz - Lista de Exercícios Resolvida
Questão 1
Uma espira circular move-se de baixo para cima na direção de um imã permanente fixo, assim como na figura abaixo.
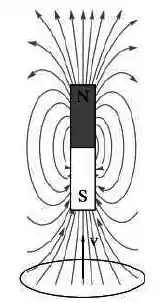
Vista de cima a corrente no fio será:
no sentido horário e a força na espira será para cima
no sentido anti-horário e a força na espira será para cima
no sentido horário e a força na espira será para baixo
no sentido anti-horário e a força na espira será para baixo
no sentido horário e a força na espira será zero
no sentido anti-horário e a força na espira será zero
Ver solução completaQuestão 2
Um solenóide longo tem um diâmetro de . Quando o solenóide é percorrido por uma corrente , um campo magnético uniforme de módulo é produzido no seu interior.
Através de uma diminuição da corrente o campo magnético é reduzido a uma taxa de . Determine o módulo do campo elétrico induzido a e a a de distância do eixo do solenóide.
Ver solução completaQuestão 3
Na figura abaixo o fluxo de campo magnético na espira aumenta de acordo com a equação , onde está em miliwebers e em segundos.
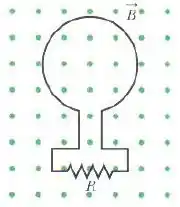
Qual é o módulo da força eletromotriz induzida na espira no instante ?
O sentido da corrente no resistor é para a direita ou para a esquerda?
Ver solução completaQuestão 4
A figura abaixo mostra duas regiões circulares, e , de raios e .
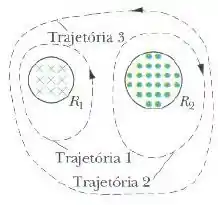
Em existe um campo magnético uniforme de módulo dirigido para dentro do papel, e em existe um campo magnético uniforme de módulo dirigido para fora do papel (ignore os efeitos de borda).
Os dois campos estão diminuindo à taxa de . Calcule o valor de para a trajetória 1; para a trajetória 2; para trajetória 3.
Ver solução completaQuestão 5
Uma espira circular de de diâmetro, feita de fio de cobre nº 10 (diâmetro igual a ), é colocada num campo magnético uniforme de modo que o seu plano fique perpendicular ao vetor . Qual deve ser a taxa de variação de com o tempo para que a corrente induzida na espira seja igual a ? Assuma que a resistividade do cobre vale
Ver solução completaQuestão 6
Uma região circular no plano é atravessada por um campo magnético uniforme orientado no sentido positivo do eixo . O módulo do campo (em teslas) aumenta com o tempo (em segundos) de acordo com a equação , onde é uma constante.
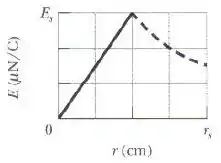
A figura acima mostra o módulo do campo elétrico criado por esse aumento do campo magnético em função radial ; a escala do eixo vertical é definida por , e a escala do eixo horizontal é definida por .
Determine o valor de .
Ver solução completaQuestão 7
A figura abaixo mostra duas espiras de fio em forma de anel, que tem o mesmo eixo. O anel menor está acima do maior, a uma distância que é grande, comparada com o raio , do anel maior. Em consequência, com a passagem da corrente pelo anel maior (veja figura), o campo magnético correspondente é aproximadamente constante através da área plana , limitada pelo anel menor. Suponha agora que a distância não seja fixa, mas que varie na razão constante
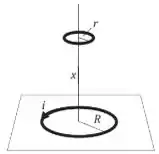
(a) Determinar o fluxo magnético através da área limitada pelo anel menor em função de .
(b) Calcular a f.e.m. gerada no anel menor, no instante em que for igual a .
(c) Determinar o sentido da corrente induzida no anel menor, se .
Ver solução completaQuestão 8
Faz-se girar uma bobina retangular, contando espiras de comprimento e largura , com uma frequência na presença de um campo magnético uniforme , como mostra a figura abaixo.
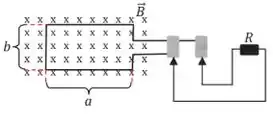
(a) Mostre que a f.e.m. induzida que aparece na bobina é dada por:
(b) Projete uma bobina para a qual seja igual a , quando girada revoluções por segundo, na presença de um campo magnético de
Ver solução completaQuestão 9
O campo magnético de um imã cilíndrico com de diâmetro varia senoidalmente entre e com uma frequência de .
Qual é a amplitude do campo elétrico induzido por essa variação a uma distância de do eixo cilíndrico?
Ver solução completaQuestão 10
Um pedaço de fio condutor ôhmico isolado é torcido de modo a constituir um circuito em forma de oito. Por razão de simplicidade, modele as duas metades da figura de oito como circunferências de círculo. O raio do círculo superior é e o do inferior é . O circuito completo é puramente resistivo (com capacitância e autoindutância desprezíveis), tendo resistência . A partir de um campo magnético uniforme, mas não estacionário
Onde é aplicado perpendicularmente ao plano dos dois circuitos, conforme mostrado na figura.
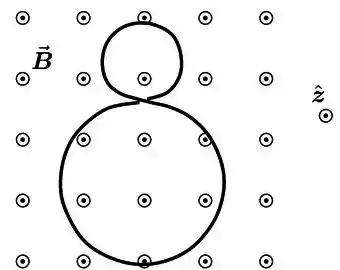
- Para determino o fluxo total através do circuito.
- Para determine o sentido da corrente elétrica induzida ao longo do fio indicando-o claramente em cada uma das circunferências, seja por intermédio de uma seta, seja pelas expressões horário ou anti-horário.
- Para determine o módulo da intensidade da corrente elétrica induzida no fio.
Questão 11
O campo magnético em todos os pontos de uma região cilíndrica de raio é uniforme e direcionado para dentro da página, variando com o tempo segundo , onde é uma constante positiva.
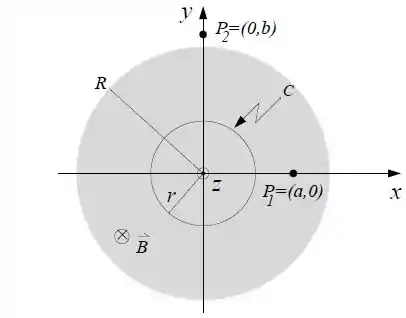
Determine a circulação do campo elétrico, , ao longo do círculo de raio mostrado na figura, percorrido no sentido anti-horário.
Determine o vetor campo elétrico (módulo, direção e sentido) nos pontos e da figura, onde e .
Ver solução completaQuestão 12
A figura abaixo ilustra um fio retilíneo infinito percorrido por uma corrente elétrica . Uma barra condutora móvel, de comprimento , move-se para a esquerda com velocidade constante entre dois trilhos horizontais. Os trilhos são paralelos entre si e também paralelos ao fio infinito. A extremidade direita dos trilhos é conectada a uma barra condutora vertical fixa, de tal forma que o conjunto (ou seja, os trilhos e a barra fixa) forma uma espira retangular condutora . O trilho superior encontra-se a uma distância do fio infinito.
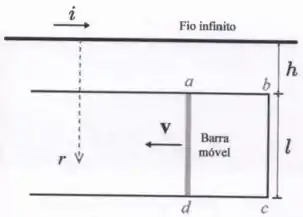
- Usando a lei de Ampère, calcule o módulo do campo magnético gerado pelo infinito a uma distância arbitrária do mesmo.
- Calcule o módulo da força eletromotriz induzida na espira retangular .
- O sentido da corrente induzida na espira retangular será horário ou anti-horário? Justifique, sucintamente, sua resposta.
Questão 13
Uma barra de comprimento e resistência é colocada sobre dois trilhos numa região de campo magnético uniforme cujo módulo é . Os trilhos estão ligados a uma fonte de tensão . Determine a corrente que flui pelo condutor quando:
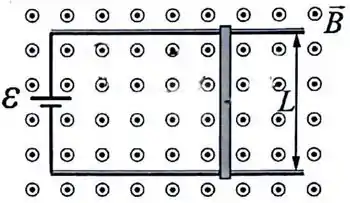
(a) A barra está em repouso
(b) A barra está se movendo para direita com uma velocidade
(c) Em que sentido e com que velocidade devemos mover o condutor para que a corrente através dele seja nula?
(d) Em que sentido e com que velocidade devemos mover o condutor para que o módulo da corrente através dele seja o mesmo módulo da corrente que o atravessava quando ele estava em repouso?
Ver solução completaQuestão 14
Um pedaço de fio condutor ôhmico isolado é torcido de modo a constituir um circuito em forma de oito. Por razão de simplicidade, modele as duas metades da figura de oito como circunferências de círculo. O raio do círculo superior é e o do inferior é . O circuito completo é puramente resistivo (com capacitância e autoindutância desprezíveis), tendo resistência . A partir de um campo magnético uniforme mas não estacionário
Onde é aplicado perpendicularmente ao plano dos dois circuitos, conforme mostrado na figura.
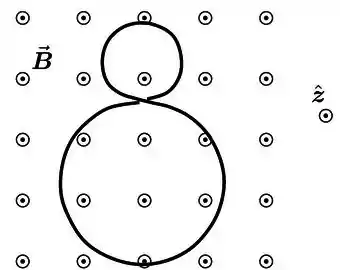
- Para determino o fluxo total através do circuito.
- Para determine o sentido da corrente elétrica induzida ao longo do fio indicando-o claramente em cada uma das circunferências, seja por intermédio de uma seta, seja pelas expressões horário ou anti-horário.
- Para determine o módulo da intensidade da corrente elétrica induzida no fio.
Questão 15
Uma espira retangular, condutora, se move numa região de campo magnético gerado por um fio retilíneo muito longo, transportando uma corrente estacionária, como mostra a figura. A espira percorre a trajetória . Determine o sentido da corrente induzida ao longo da espira em cada uma das partes da trajetória.
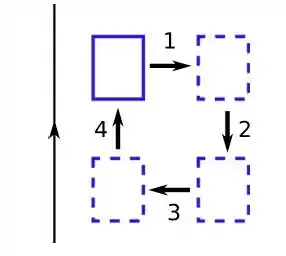
- Horário, não há corrente, anti-horário, não há corrente
- Anti-horário, não há corrente, horário, não há corrente
- não há corrente, horário, não há corrente, anti-horário
- não há corrente, anti-horário, não há corrente, horário
- horário, não há corrente, não há corrente, anti-horário
- anti-horário, não há corrente, anti-horário, não há corrente
Questão 16
Uma espira circular move-se de baixo para cima na direção de um imã permanente fixo, assim como na figura abaixo.
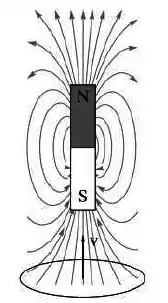
Vista de cima a corrente no fio será:
no sentido horário e a força na espira será para cima
no sentido anti-horário e a força na espira será para cima
no sentido horário e a força na espira será para baixo
no sentido anti-horário e a força na espira será para baixo
no sentido horário e a força na espira será zero
no sentido anti-horário e a força na espira será zero
Ver solução completaQuestão 17
Considere um trilho condutor em forma de , ao lado de um fio infinito que transporta uma corrente estacionária , como indica a figura (onde indicamos ainda os vetores unitários das coordenadas cilíndricas , e ).
Suponha que uma haste metálica de comprimento é colocada entre os dois braços do trilho formando um circuito fechado, e que uma força externa faz a haste deslizar sobre o condutor com velocidade constante .
Despreze as forças de atrito e a resistência do trilho, e considere que a resistência da haste é igual a . Despreze ainda qualquer efeito auto indutivo e capacitivo.
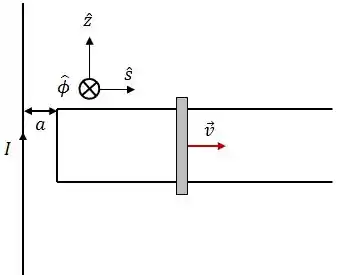
Qual a direção do campo magnético gerado pelo fio infinito, num ponto arbitrário? Argumente detalhadamente, utilizando seus conhecimentos de magnetismo e/ou argumentos de simetria.
Obtenha o módulo do campo magnético gerado pelo fio, num ponto arbitrário. Note que, dependendo do argumento utilizado, argumentos de simetria se farão necessários.
Calcule o fluxo magnético gerado pelo campo magnético do fio infinito no circuito (trilho + haste).
Determine o módulo e o sentido da corrente induzida no circuito. Novamente, argumente detalhadamente, utilizando seus conhecimentos de magnetismo.
Calcule a força magnética sobre a haste quando ela está a uma distância do fio infinito.
Ver solução completaQuestão 18
Uma espira retangular tem comprimento , largura e resistência .
Suponha que numa região do espaço exista um campo magnético que cresce linearmente com , isto é, aumenta à medida que se afasta de a partir da origem, e é dado por , onde é uma constante. Este campo magnético está na direção de (”entrando no plano da página”).
A espira é então imersa nessa região, como mostra a figura abaixo, onde é a distância do centro da espira até o eixo .
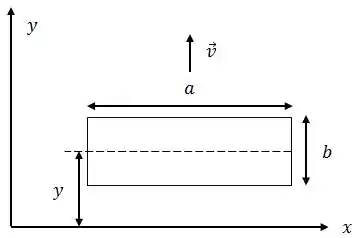
Determine:
- O fluxo do campo magnético através da espira.
- A corrente induzida na espira à medida que esta se afasta do eixo com velocidade constante ao longo de .
- O sentido da corrente induzida na espira (justificar a resposta).
Questão 19
Considere uma superfície formada por três quadrados de lado : e , como é mostrado na figura. O quadrado é paralelo ao plano . Na região da superfície existe um campo magnético uniforme .
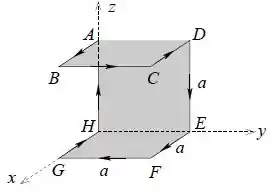
- Calcule o fluxo magnético através da superfície para .
- Calcule o fluxo magnético através da superfície para .
- Considere com . Calcule a integral de linha do campo elétrico ao longo do caminho fechado na fronteira de percorrido no sentido indicado na figura.
Questão 20
A figura ao lado mostra a seção transversal de uma região cilíndrica de raio , coaxial com o eixo de um sistema de coordenadas, onde existe um campo magnético uniforme dado por
constante
de modo que e .
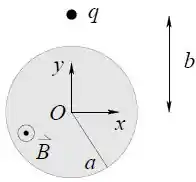
Obtenha o vetor campo elétrico induzido em todo o espaço, em função de , e .
A figura também mostra uma partícula com carga . Para a partícula na posição indicada na figura , obtenha o vetor força elétrica que atua sobre ela. Calcule também o vetor torque da força elétrica em relação à origem do sistema de coordenadas. Expresse os vetores sob a forma cartesiana, isto é, em termos das componentes nas direções , e .
Ver solução completaQuestão 21
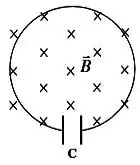
Um campo magnético homogêneo atravessa uma espira de área no sentido indicado pela figura. A instensidade do campo varia com o tempo da forma , onde está em segundos e em tesla. Para os tempos , e , determine:
- A diferença de potencial sobre o capacitor.
- A polarização do capacitor.
Questão 22
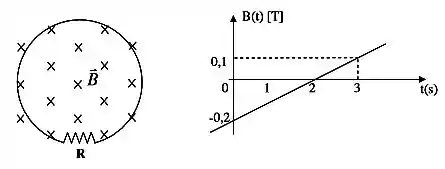
Uma espira de área , conectada a uma resistência de , é aplicado aum campo magnético perpendicular à sua área, que varia no tempo conforme o gráfico (considere a intensidade positiva quando o campo está para fora do papel). A figura abaixo representa o instante inicial. Determine para , , :
- O sentido da corrente induzida na espira.
- O valor da corrente induzida.
Questão 23
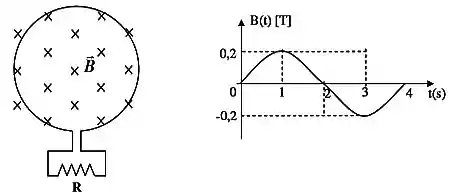
O circuito abaixo é composto de uma resistência () e uma espira circular (área ). A espira circular se encontra imersa em uma região do espaço que contém um campo magnético aplicado perpendicular a sua área (o sentido do campo é entrando no papel). Considere que a intensidade do campo varia no tempo conforme o gráfico abaixo e calcule para e segundos:
- O sentido da corrente induzida na espira.
- O valor da corrente induzida.
Questão 24
A figura abaixo mostra uma espira retangular, de largura e comprimento , e um fio longo que transporta uma corrente de acordo com a disposição da figura. A distância do fio ao lado maior da espira é .
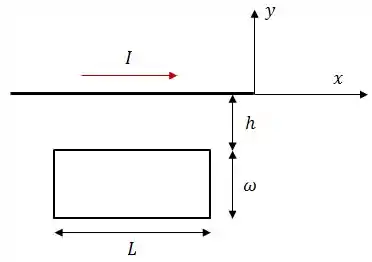
Determine:
O fluxo magnético através da espira;
Suponha agora que a corrente varie com o tempo de acordo com a expressão , onde e são constantes. Detemine:
A fem induzida na espira, se , e ;
O sentido da corrente induzida (explicar);
Ver solução completaQuestão 25
Uma espira quadrada de fio condutor está montada sobre um suporte deslizante, que se move sem atrito em um trilho de ar, com velocidade inicial . Quando a parte dianteira da espira entra na região em que existe campo magnético , apontando para dentro da página como mostrado na figura,
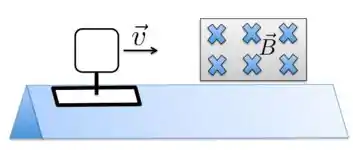
- Aparece uma corrente no sentido horário na espira, e o suporte desacelera.
- Aparece uma corrente no sentido anti-horário na espira e o suporte desacelera.
- Aparece uma corrente no sentido horário na espira e o suporte acelera.
- Aparece uma corrente no sentido anti-horário na espira e o suporte acelera.
- Não aparece corrente na espira e o suporte se move com velocidade .
Questão 28
Um solenoide ideal, com voltas por unidade de comprimento (axial) e seção transversal circular de raio , é percorrido por uma corrente elétrica cuja intensidade varia no tempo de acordo com (). Dentro do solenoide, em um plano perpendicular ao seu eixo, com raio , coloca-se uma espira circular condutora de resistência . A autoindutância da espira e a indutância mutua entre essa e o solenoide são desprezíveis. Considere, ademais, que a lei de Ampére usual possa ser aplicada.
- Determine o vetor campo magnético dentro do solenoide, produzido pela corrente .
- Qual é a intensidade da corrente induzida na espira?
- Qual é o sentido de tal corrente induzida?
- Determine o vetor campo elétrico induzido na espira.
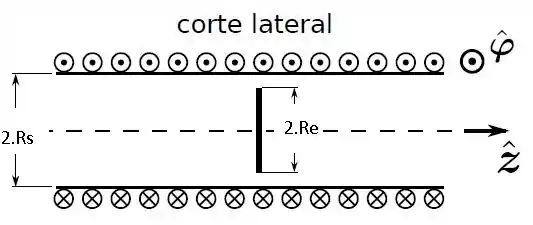
Questão 29
Uma barra condutora vertical de comprimento sob ação de uma força externa , se move na horizontal com velocidade constante , deslizando sem atrito sobre 2 condutores paralelos fixos, formando um circuito fechado com uma terceira barra fixa de resistência . Simultaneamente, um fio horizontal infinito está paralelo aos dois condutores e a um distância do condutor mais próximo. Por este fio passa uma corrente constante no sentido negativo do eixo . Sabendo que o módulo do campo magnético produzido por um fio com corrente a uma distância é dado por , determine:
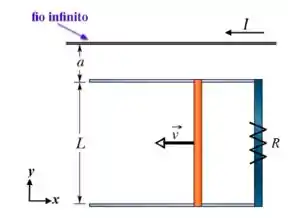
- O módulo da força eletromotriz induzida no circuito.
- O sentido da corrente induzida no circuito e justifique sua resposta.
- Determine o vetor força externa , em termos dos parâmetros geométricos do problema e demais dados no enunciado.
Questão 30
Uma espira circular de raio r está imersa em um campo magnético uniforme e estacionário
. Ela gira com velocidade angular constante em torno do eixo de um sistema de coordenadas, conforme a figura abaixo. Considere que, no instante , a espira encontra-se sobre o plano , centrada na origem, e o seu vetor área aponta no mesmo sentido do campo. Sobre essa situação, considere as afirmativas abaixo:
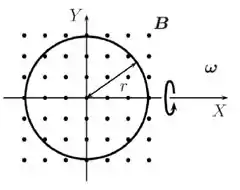
(I) O fluxo de campo magnético através da espira varia com o tempo na forma .
(II) A força eletromotriz induzida na espira é máxima no instante .
(III) O sentido da corrente induzida na espira é sempre anti-horário quando visto da direção positiva para a negativa no eixo .
São VERDADEIRAS as afirmativas:
(a) Apenas I
(b) Apenas II
(c) Apenas III
(d) Apenas I e II
(e) Apenas I e III
(f) Apenas II e III
(g) I, II e III
(h) Nenhuma delas
Ver solução completaQuestão 31
Considere um solenoide infinito de raio com espiras por unidade de comprimento por onde passa uma corrente
onde é uma constante com dimensão de inverso de tempo.
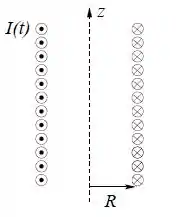
Dado: o vetor campo magnético do solenoide é .
Calcule o vetor campo elétrico no exterior do solenoide para .
Calcule o vetor campo elétrico no interior do solenoide para .
Considere uma partícula com carga e massa que, no instante , está parada a uma distância do eixo do solenoide conforme a figura. Calcule o vetor aceleração desta partícula em .
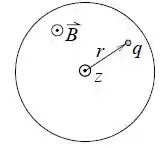
Corte transversal
Ver solução completaQuestão 32
Considere uma espira colocada no plano . Em um dado instante, uma pessoa coloca um ímã no eixo de simetria da espira (inicialmente acima da espira) e o aproxima dela, conforme ilustra a figura abaixo. Ela então observa o surgimento de uma corrente induzida no sentido anti-horário. O polo corresponde a qual polo ímã, norte ou sul? A força magnética que surge entre o ímã e a espira é atrativa ou repulsiva? (Utilize a convenção de que o polo norte é o polo do qual saem as linhas de campo magnético).
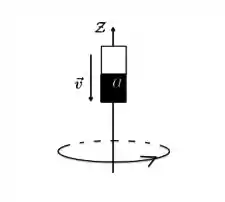
(a) Norte, repulsiva.
(b) Norte, atrativa.
(c) Sul, repulsiva.
(d) Sul, atrativa.
Ver solução completaQuestão 33
Uma espira condutora quadrada é posicionada sobre o mesmo plano de um fio condutor fino, retilíneo e infinito, como mostrado na figura abaixo. Ela é mantida fixa com dois de seus lados paralelos ao fio. Nessa situação, observa-se que surge uma corrente induzida na espira com sentido anti-horário e que o fio exerce uma força magnética atrativa sobre a espira. A partir dessas observações, podemos afirmar que:
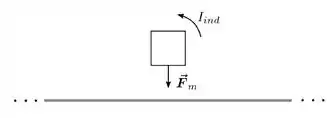
- Uma corrente não-estacionária flui da esquerda para a direita ao longo do fio, e sua intensidade diminui com o tempo.
- Uma corrente não-estacionária flui da esquerda para a direita ao longo do fio, e sua intensidade aumenta com o tempo.
- Uma corrente não-estacionária flui da direita para a esquerda ao longo do fio, e sua intensidade diminui com o tempo.
- Uma corrente não-estacionária flui da direita para a esquerda ao longo do fio, e sua intensidade aumenta com o tempo.
- Uma corrente estacionária flui da esquerda para a direita ao longo do fio.
- Uma corrente estacionária flui da direita para a esquerda ao longo do fio.
Questão 34
A figura mostra uma espira condutora quadrada de lado , localizada no plano . A espira desloca-se ao longo do eixo com velocidade de módulo , onde é a distância da extremidade esquerda da espira ao eixo . Tal espira está submetida a um campo magnético variável no espaço e aponta para fora do plano da página e cujo módulo é dado por , onde é uma constante positiva. Nestas circunstancias, determine:
(a) O módulo do fluxo magnético através da espira
(b) O módulo da força eletromotriz induzida na espira
(c) O sentido de circulação da corrente induzida (horário ou anti-horário). Justifique a sua resposta.
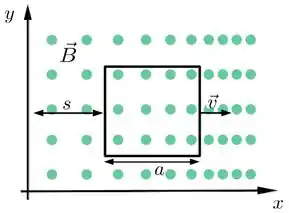
Questão 35
Uma espira retangular, rígida, condutora e um fio retilíneo, infinito, pelo qual passa uma corrente quase estacionária () encontram-se num mesmo plano, . No instante a espira possui velocidade () como mostrado na figura abaixo.
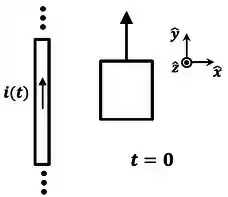
Desconsiderando o efeito da gravidade, qual gráfico melhor representa o movimento da espira logo após o instante ?
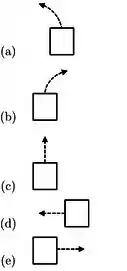
(f) Nenhuma das anteriores
Ver solução completaQuestão 36
Uma espira circular condutora, de raio e resistência elétrica gira com velocidade angular constante em torno do eixo de um sistema de coordenadas, como mostrado na figura abaixo. Ela está imersa em uma região de campo magnético constante . Considere que, no instante , a espira encontra-se sobre o plano , com seu centro sobre a origem e com o vetor unitário normal ao seu plano apontando no mesmo sentido do campo.
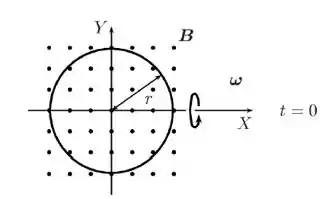
- Determine o fluxo magnético através da área da definida pela espira em um instante qualquer.
- Determine a corrente induzida sobre a espira no mesmo instante.
- Determine o torque que o campo magnético exerce sobre a espira no mesmo instante.
Questão 37
Complete a seguinte afirmação: a corrente induzida em uma bobina pelo aumento do fluxo magnético
- Tem o mesmo sentido que o campo magnético;
- Tem sentido oposto ao do campo magnético;
- É tal que o campo magnético produzido pela corrente torna o fluxo total igual a zero;
- Tem um sentido tal que o campo magnético produzido pela corrente reduz o fluxo magnético total;
- Tem um sentido tal que o campo magnético produzido pela corrente aumenta o fluxo magnético total.
Questão 38
Considere dois circuitos fechados ôhmicos, 1 e 2, puramente resistivos, de mesma resistência , no plano cartesiano , muito afastados um do outro, com a forma de um “oito” torcido, de modo que, para o circuito , suas partes, de baixo e de cima, têm a mesma área , ao passo que, para o circuito , a área da parte de baixo continua sendo , mas aquela da de cima é o triplo. Tais circuitos estão sujeitos ao campo magnético , com . Assinale a alternativa que melhor indica quais são os módulos das intensidades de corrente induzida em tais circuitos e as correspondentes orientações nas suas partes de cima.
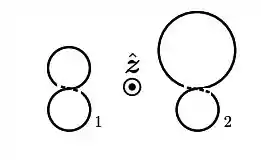
(a) , horário.
(b) , anti-horário.
(c) , horário; , horário.
(d) , anti-horário; , anti-horário.
(e) , horário; , horário.
(f) , anti-horário; , anti-horário.
Ver solução completaQuestão 39
A figura mostra uma espira condutora circular de raio , localizada no plano . A espira está submetida a um campo magnético variável no tempo e no espaço dado por , onde e são constantes positivas e é a distância radial até o centro da espira. O campo magnético atua na região hachurada da figura, sendo perpendicular à página e apontando para fora da mesma. Nestas circunstâncias, determine:
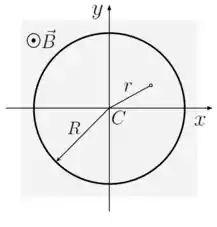
(a) O fluxo magnético através da espira.
(b) A força eletromotriz induzida na espira.
(c) O sentido de circulação da corrente induzida (horário ou anti-horário) num instante de tempo finito . Justifique sua resposta.
Ver solução completaQuestão 40
Um solenoide muito longo, coaxial com o eixo , tem comprimento , raio e espiras no total. O solenoide é colocado no vácuo. Desprezando efeitos de borda, o campo dentro do solenoide é , onde é a corrente através das espiras.
(a) (1,0 ponto) Calcula a indutância do solenoide.
(b) (1,5 ponto) Uma corrente variável no tempo dada por percorre o solenoide. Usando a lei de Faraday, calcule o vetor campo elétrico na região , onde é a distância ao eixo do solenoide.
Ver solução completaQuestão 41
A figura mostra uma barra retilínea condutora, de massa , comprimento e resistência elétrica , movendo-se com uma velocidade constante ao longo de trilhos condutores, retilíneos horizontais, fixos.
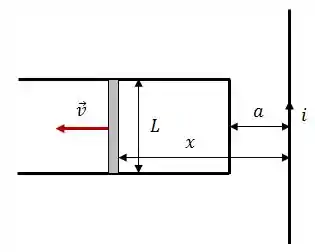
Tal circuito está sob ação de um campo magnético gerado por uma corrente elétrica estacionária fluindo por um fio retilíneo longo, paralelo à barra e no mesmo plano do circuito.
A resistência dos trilhos, assim como a capacitância e a autoindutância do circuito e a indutância mútua entre o circuito e o fio retilíneo (de corrente ) podem e devem ser desprezadas.
Obtenha uma expressão para a corrente elétrica no circuito, , como função da distância da barra ao fio, explicitando, ademais, o sentido de tal corrente.
[Sugestão: não precisa deduzir o campo magnético de uma corrente retilínea estacionária, muito longa.]
Obtenha uma expressão para a taxa temporal de dissipação de energia, pelo efeito Joule, na barra, como função de .
Obtenha uma expressão para a força externa que precisa ser aplicada à barra para manter a sua velocidade constante.
Ver solução completaQuestão 42
Um solenóide real, de comprimento e seção transversal circular de raio , é colocado próximo a uma espira condutora de raio e espessura muito menor que . O plano da espira é posicionado paralelamente ao plano de uma seção transversal do solenóide, e ambos possuem o mesmo eixo de simetria , conforme mostrado na figura abaixo.
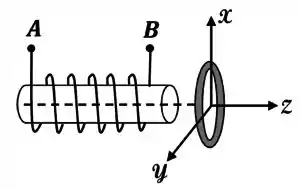
Considere as seguintes situações:
- Uma corrente quase-estacionária, que aumenta proporcionalmente com o tempo, circula no solenóide de para .
- Uma corrente quase-estacionária, que aumenta proporcionalmente com o tempo, circula no solenóide de para .
O que acontecerá com a espira condutora nas duas situações acima?
- Em ambas as situações, será repelida pelo solenóide.
- Em será atraída e em será repelida pelo solenóide
- Em ambas as situações, será atraída pelo solenóide.
- Em será repelida e em será atraída pelo solenóide.
- Não será atraída nem repelida em nenhuma das situações.
Questão 43
O campo elétrico na região considerada na figura é dado por sendo uma constante positiva.
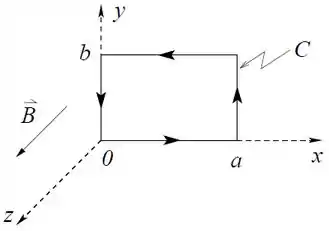
Calcule a integral de linha ao longo do retângulo de largura e altura , orientado como é mostrado na figura.
Além do campo elétrico na região considerada há também um campo magnético uniforme cuja intensidade depende do tempo. Em , . Utilizando a Lei de Faraday na forma integral, determine .
Ver solução completaQuestão 44
Um solenoide longo de comprimento , seção reta circular de raio e com espiras é percorrido por uma corrente . O módulo do campo magnético no interior solenoide é dado por .
Calcule o vetor campo elétrico no interior do solenoide.
Calcule o vetor campo elétrico fora do solenoide.
Ver solução completaQuestão 45
Um campo magnético uniforme está dirigido para fora da página, como mostrado. Uma espira condutora de área está no plano da página. Em um dado instante, o módulo do campo magnético é e ele está diminuindo à taxa de . O módulo e o sentido da fem induzida na espira nesse instante são, respectivamente:
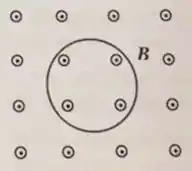
- , horário;
- , anti-horário;
- , anti-horário;
- , horário;
- , anti-horário;
Questão 46
A figura abaixo mostra um bastão condutor de comprimento sendo puxado ao longo dos trilhos condutores com velocidade constante de . Todo o sistema está imerso em um campo magnético perpendicular entrando na página e de módulo igual a . Sabendo que a resistência total do circuito é , a corrente induzida e o seu sentido são, respectivamente
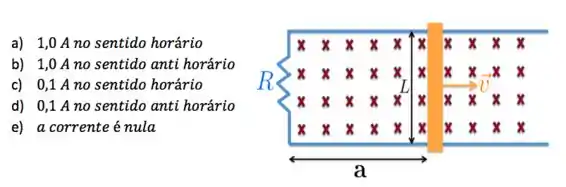
Questão 47
Um fio fino, retilíneo e infinito transporta uma corrente estacionária de intensidade , no sentido indicado na figura abaixo. Três espiras quadradas, , e , posicionadas no mesmo plano do fio e com dois de seus lados paralelos ao mesmo, se movem com velocidade constante nos sentidos indicados, preservando as suas orientações. As espiras e são condutoras, enquanto a espira é isolante. Responda, justificando cada resposta:
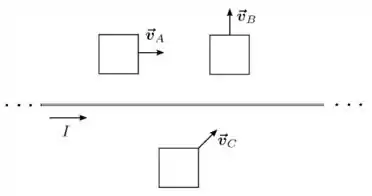
- Haverá corrente induzida sobre a espira ? Se sim, indique o seu sentido.
- Haverá força eletromotriz induzida sobre a espira ? Se sim, indique o seu sentido.
- O fio exercerá força magnética sobre a espira ? Se sim, indique o seu sentido.
Questão 48
Uma espira condutora retangular, de altura , largura e resistência elétrica está situada no plano - como indicado na figura ao lado. A espira está imersa em um campo magnético , onde denota o vetor unitário ao longo do eixo , , e é uma constante positiva.
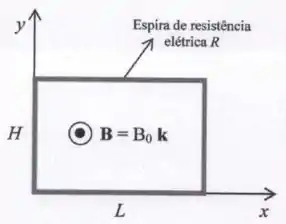
- Calcule o módulo do fluxo magnético através da espira.
- Calcule o módulo da corrente induzida na espira. Além disso, determine e justifique o sentido (horário ou anti-horário) da corrente induzida.
- Determine o sentido (horário ou anti-horário) do campo elétrico induzido na espira.
Questão 49
Um trilho condutor em forma de semicircunferência de raio está imerso numa região com campo magnético externo de módulo (uniforme e constante), de direção perpendicular à página e com sentido saindo do papel. Um circuito elétrico de resistência total constante é completado por dois trilhos condutores retilíneos que partem do centro da circunferência: um horizontal, fixo, e outro móvel, que faz com o primeiro um ângulo variável [ , s].
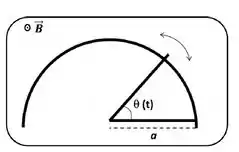
- Calcule a induzida no circuito como função do tempo, . [Sugestão: Lembre que a área de um setor circular de raio e ângulo em radianos é dada por ] .
- Calcule o instante em que a corrente induzida se anula. Nos intervalos e , qual é o sentido da corrente no circuito, horário ou anti-horário? (Justifique.)
- Calcule o valor máximo que a corrente assume no intervalo .
- Determine uma função para que a corrente induzida no circuito seja sempre nula.
Considere ainda a mesma função do enunciado principal, mas que agora o campo magnético externo varie no tempo em vez de ser constante.
Questão 50
Considere um capacitor de placas circulares e paralelas de raio , cuja distância entre elas é muito menor que . Ele encontra-se inicialmente descarregado e começa então a ser carregado por meio de uma corrente cuja intensidade diminui com o tempo, fornecida por fios conectados às placas. Sobre essa situação, considere as afirmativas abaixo:
- O campo elétrico gerado entre as placas do capacitor é não-estacionário.
- O campo magnético gerado entre as placas do capacitor é não-estacionário.
- As linhas do campo magnético gerado entre as placas do capacitor serão circulares e paralelas às placas.
São CORRETAS as afirmativas:
- Somente
- Somente
- Somente
- , e
- Somente e
- Somente e
- Somente e
- Nenhuma delas
Questão 51
A figura abaixo mostra uma espira quadrada de lado e resistência elétrica , que encontra-se nas proximidades de um fio infinito retilíneo, percorrido por uma corrente elétrica constante . O fio é direcionado paralelamente aos lados verticais da espira quadrada. Note que o fio e a espira são coplanares. Sabe-se que a espira desloca-se com velocidade constante , na direção perpendicular ao fio. A distância do fio infinito à extremidade esquerda da espira é dada por . Note que é uma função do tempo. Todo o sistema está imerso no vácuo, cuja constante de permeabilidade magnética é dada por .
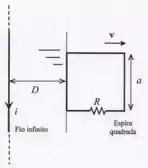
- Calcule o módulo do fluxo magnético gerado pelo campo magnético do fio infinito através da espira.
- Calcule o módulo e o sentido (horário ou anti-horário) da corrente elétrica induzida na espira.
- Neste item, responda às mesmas perguntas feitas no item b), agora supondo que a espira se move com velocidade paralela ao fio infinito (observe que neste caso a distância não varia com o tempo).
Questão 52
Indique com V se a afirmação é verdadeira, ou F, se falsa.
Uma partícula carregada pode ter um movimento retilíneo uniforme em uma região do espaço contendo campos elétrico e magnético uniformes, se eles forem perpendiculares entre si.
Quando uma espira condutora e outra isolante, ambas rígidas e em repouso, são posicionadas perpendicularmente a um campo magnético uniforme que varia no tempo, surge uma força eletromotriz induzida apenas na espira condutora.
Ao fazermos passar uma corrente estacionária através das espiras helicoidais de uma mola feita de material condutor, as espiras se aproximam, como se a mola fosse comprimida.
Em um fio condutor ôhmico dado, ao dobrarmos a diferença de potencial entre suas extremidades, dobramos sua resistência.
O fluxo do campo magnético da Terra através da superfície correspondente ao território brasileiro é igual, em módulo, ao fluxo do campo magnético da Terra através da superfície correspondente a todo o resto do globo terrestre.
A lei de Ampère afirma que, para correntes estacionárias, o fluxo do campo magnético através de uma superfície é igual a vezes a corrente que atravessa .
Uma espira retangular de metal, originalmente sem corrente, está próxima de um fio longo e retilíneo, que transporta corrente, com dois de seus lados paralelos ao fio. O fio e a espira se encontram no mesmo plano. Quando a corrente do fio está diminuindo, a espira é atraída pelo fio.
Para um condutor usual, como o cobre, o aumento da temperatura aumenta as vibrações moleculares, provocando maior espalhamento dos elétrons, o que faz com que sua resistividade diminua.
Se a circulação do campo magnético ao longo de um caminho fechado for nula, não haverá nenhuma partícula carregada em movimento atravessando uma superfície aberta delimitada pela curva que descreve esse caminho.
A força magnética sobre uma espira carregando uma corrente estacionária, localizada em uma região de campo magnético uniforme é sempre nula, independentemente do formato da espira.
Ver solução completaQuestão 53
Considere dois cilindros ocos, de mesmo comprimento, o primeiro de (isolante), , e o segundo de alumínio (condutor não magnético), , ambos posicionados na vertical com relação ao solo.
Desejamos soltar duas barras, uma imantada, , e a outra não imantada, , no interior desses cilindros, simultaneamente. O que acontece quando:
soltamos a barra no tubo e a barra no tubo ; e soltamos a barra no tubo e a barra no tubo ?
Suponha que o experimento é feito na superfície da Terra e despreze a resistência do ar.
Ambas as barras chegam ao mesmo tempo ao solo; Ambas s barras chegam ao mesmo tempo ao solo.
A barra chega primeiro ao solo; Ambas as barras chegam ao mesmo tempo ao solo.
A barra chega primeiro ao solo; A barra chega primeiro ao solo.
A barra chega primeiro ao solo; Ambas as barras chegam ao mesmo tempo ao solo.
Ambas as barras chegam ao mesmo tempo ao solo; A barra chega primeiro ao solo.
Ver solução completaQuestão 54
Considere as afirmativas abaixo:
A corrente induzida num circuito, devido à variação temporal do fluxo do campo magnético externo , surge sempre no sentido de gerar um campo magnético induzido oposto a .
Um solenoide infinito, de raio , paralelo ao eixo , é percorrido por uma corrente constante variável . Uma espira é colocada fora do solenoide, a uma distância de seu eixo. Podemos afirmar que a corrente induzida na espira gira no sentido anti-horário.
Duas espiras condutoras (do mesmo material) e , de raios respectivos e , são postas numa região de campo magnético uniforme, porém não constante, dado por . Considerando o fenômeno de indução, podemos afirmar que a corrente induzida em é o dobro da induzida em .
Quais são as afirmativas verdadeiras?
e
e
e
Nenhuma
Todas
Ver solução completaQuestão 55
Na figura abaixo, o fio retilíneo longo transporta uma corrente e a espira retangular, de resistência , transporta uma corrente nos sentidos indicados. O fio e a espira encontram-se no mesmo plano.
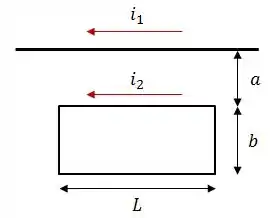
Calcule:
O vetor força magnética resultante que atua sobre a espira;
O fluxo do campo magnético produzido pela corrente através da área da espira;
Se a corrente crescer a uma taxa constante , determine o valor e o sentido
da corrente induzida na espira;
Ver solução completaQuestão 56
Considere dois anéis circulares em repouso: um condutor e outro isolante . Ambos estão sujeitos a campos magnéticos não estacionários orientados para dentro do plano dos anéis. Quanto ao campo elétrico induzido e à corrente elétrica induzida , nos anéis, podemos afirmar que:
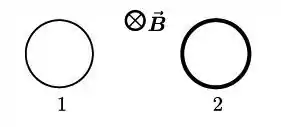
- , ; ,
- , ; ,
- , ; ,
- , ; ,
- , ; ,
Questão 57
Analise as seguintes afirmativas:
Em uma dada região, existe, originalmente, um campo magnético constante (estacionário e uniforme) e uma superfície aberta plana. Se o módulo de tal campo for dobrado e a área da superfície for quadruplicada, mantendo-se plana e com a mesma orientação, então o fluxo de campo magnético, através da nova superfície, cresce por um fator quatro, em comparação com a antiga superfície;
De acordo com a lei de Faraday, a condição necessária e suficiente para que uma força eletromotriz seja induzida em um circuito fechado é a presença no circuito de um campo magnético que varia com o tempo;
Se uma espira condutora próxima a um imã começa a afastar-se desse, então surge uma força repulsiva entre o imã e a espira.
Qual(is) é(são) verdadeira(s)?
Apenas a .
Apenas a .
Apenas a .
Apenas a e a .
Apenas a e a .
Apenas a e a .
Todas são verdadeiras
Nenhuma é verdadeira.
Ver solução completaQuestão 59
As figuras mostram dois solenoides em três movimentos diferentes, ambos com velocidade .
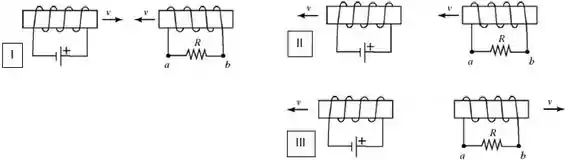
A corrente induzida através da resistência será:
I – de A para B, II – de B para A, III – de A para B
I – de A para B, II – corrente nula, III – de B para A
I – de B para A, II – de B para A, III – de B para A
I – de A para B, II – corrente nula, III – corrente nula
I – corrente nula, II – de B para A, III – de B para A
Ver solução completaQuestão 60
Uma espira circular condutora penetra perpendicularmente e com velocidade constante em uma região de campo magnético uniforme, cujo sentido é para fora da página, tal como indicado na figura, onde são apresentadas três posições representativas: A) espira entrando na região de campo magnético; B) espira completamente imersa no campo magn��tico e C) espira saindo do campo magnético. A opção que representa o sentido da corrente induzida na espira em cada uma das posições A, B e C é:
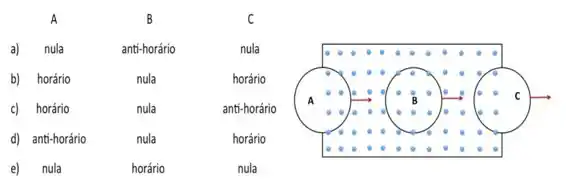
Questão 61
(Capítulo 30.4 – Exercício 2) Um material condutor elástico é esticado e usado para fazer uma espira circular com de raio, que é submetida a um campo magnético uniforme de perpendicular ao plano da espira. Ao ser liberada, a espira começa a se contrair e seu raio diminui inicialmente à taxa de . Qual é a força eletromotriz induzida na espira durante a contração?
Ver solução completaQuestão 62
Uma barra condutora fina encontra-se imersa em uma região de campo magnético constante que aponta para fora do plano do papel, como mostrada na figura abaixo. Ela gira com velocidade angular constante em sentido horário em torno de um eixo paralelo à direção do campo e que para por seu centro, que corresponde ao ponto na figura. A barra permanece perpendicular à direção do campo durante todo o movimento. Considerando os pontos , e mostrados na figura, podemos afirmar que, após estabelecido o equilíbrio de cargas no interior da barra, os potenciais elétricos nesses pontos, dados por , e , satisfazem:
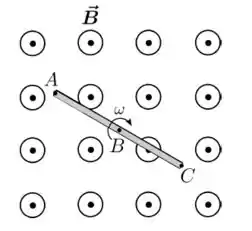
Questão 63
Na figura a seguir vemos duas espiras circulares de mesmo eixo separadas por uma distância grande comparada com . A espira de raio se encontra fixa e por ela circula uma corrente estacionária de intensidade e sentido mostrado na figura, enquanto a espira de raio se move com velocidade constante ao longo do eixo comum, podendo se aproximar ou se afastar da espira de raio .
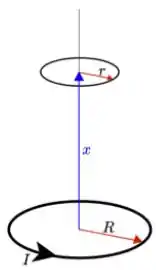
Nessa situação, podemos afirmar que:
Escolha uma:
. Se a espira de raio se afasta da espira de raio , a corrente induzida na espira de raio terá sentido oposto ao da corrente da espira de raio .
. Se a espira de raio se aproxima da espira de raio , a corrente induzida na espira de raio terá o mesmo sentido da corrente da espira de raio .
. Se a espira de raio se afasta da espira de raio , a corrente induzida na espira de raio terá o mesmo sentido da corrente da espira de raio .
. Não haverá corrente induzida na espira de raio , independentemente do sentido de seu movimento.
. A corrente induzida na espira de raio terá o mesmo sentido da corrente na espira de raio , independentemente do sentido de seu movimento.
Ver solução completaQuestão 66
A figura abaixo mostra um trilho condutor com forma de e de resistência desprezível sobre o qual uma barra curva, na forma de um semicírculo de raio , desliza sem atrito e com velocidade constante . Todo o sistema está sobre o plano e sob a ação de um campo magnético constante . A barra curva possui resistividade e seção transversal constante de área . Nos cálculos abaixo, escolha o vetor unitário normal ao plano definido pela barra curva e o trilho condutor como .
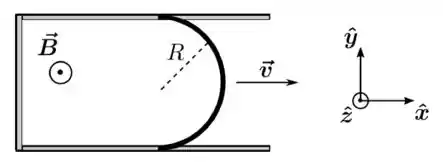
- Determine a intensidade e o sentido da corrente induzida na barra em movimento.
- Determine a força magnética (módulo, direção e sentido) que o campo magnético exerce sobre a barra devido à corrente induzida.
Questão 67
A corrente elétrica de um solenóide decresce uniformemente de seu valor inicial até zero. Durante esse tempo, gera-se um campo elétrico no interior do solenóide. Qual das seguintes afirmações sobre o campo elétrico é verdadeira?
- Não há relação entre o campo elétrico dentro do solenóide e a variação de sua corrente.
- O módulo do campo elétrico é o mesmo em qualquer ponto dentro do solenóide, mas ele decresce uniformemente com o tempo na mesma taxa de variação da corrente.
- O módulo do campo elétrico é o mesmo em qualquer ponto do solenóide e é constante no tempo
- O módulo do campo elétrico é constante no tempo, mas cresce radialmente a partir do eixo do solenóide.
- O módulo do campo elétrico é constante no tempo, mas decresce radialmente a partir do eixo do solenoide
Questão 68
Considere as seguintes afirmativas. (I) Na presença de um campo magnético estacionário, não é possível haver correntes induzidas pelo efeito Faraday. (II) Para que haja uma força eletromotriz em uma espira é necessário que o material que a compõe seja condutor. (III) É possível que a corrente induzida em uma espira pela variação temporal de um campo magnético externo crie um campo magnético no mesmo sentido do campo original. Assinale a opção que contém as afirmativas verdadeiras.
(a) Somente (III).
(b) (I) e (III).
(c) (I), (II), e (III).
(d) (I) e (II).
(e) Somente (I).
Ver solução completaQuestão 69
Um ímã cai através de uma espira metálica tal como indicado na figura abaixo. Quais serão os sentidos da corrente visto pelo observador que está abaixo da espira:
- Quando o ímã cai em direção cai em direção à espira, com o polo Norte apontando para o plano da espira.
- Quando o polo Sul se afasta do plano da espira
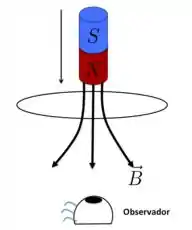
- Horário no caso I e anti-horário no caso II.
- Anti-horário nos casos I e II.
- Horário nos casos I e II.
- Anti-horário no caso I e horário no caso II.
- Não há corrente induzida nesses casos.
Questão 70
Uma espira condutora quadrada encontra-se com sua metade imersa em um campo magnético uniforme, perpendicular ao plano da espira e que aponta para fora da página. Se o campo magnético começa a diminuir rapidamente de intensidade, podemos dizer que a espira:
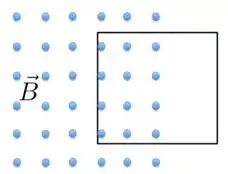
- Será empurrada para cima
- Será empurrada para baixo
- Será puxada para a esquerda em direção à região do campo magnético
- Será puxada para a direita, para fora da região do campo magnético
- A tensão nos fios aumentará, mas a espira não entrará em movimento
Questão 71
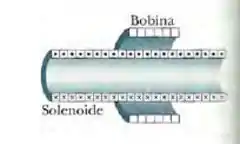
(Capítulo 30.4 – Exercício 3) Na figura 30-32, uma bobina de espiras, com de raio e uma resistência de , é coaxial com um solenoide de e de diâmetro. A corrente no solenoide diminui de para zero em um intervalo de tempo . Qual é a corrente induzida na bobina no intervalo ?
Questão 72
Uma espira com de raio e uma resistência de é submetida a um campo magnético uniforme cujo módulo varia de acorco com a figura 30-33. A escala do eixo vertical é definida por e a escala do eixo horizontal é definida por . O plano da espira é perpendicular a . Determine a força eletromotriz induzida na espira durante o intervalo de tempo (c) .

Questão 73
(Capítulo 30.4 – Exercício 27) Na Fig. 30-48, uma espira quadrada com de lado é submetida a um campo magnético, dirigido para fora do papel, cujo módulo é dado por , onde está em teslas, em segundos e em metros. Determine (a) o valor absoluto e (b) o sentido da força eletromotriz induzida na espira no instante .
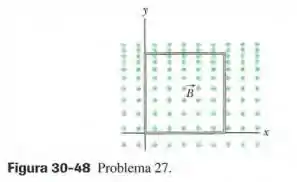
Questão 74
(Capítulo 30.4 – Exercício 10) A figura 30-37 mostra uma espira formada por um ar de semicircunferencias de de raio situadas em planos mutuamente perpendiculares. A espira foi formada dobranco uma espira plana ao longo de um diâmetro até que as duas partes ficassem perpendiculares. Um campo magnético uniforme de módulo é aplicado perpendicularmente ao diâmetro de dobra, fazendo ângulos iguais (de ) com os planos das semicircunferências. O campo magnético é reduzido para zero a uma taxa uniforme durante um intervalo de tempo de . Determine (a) o valor absoluto e (b) o sentido (horário ou anti-horário, do ponto de vista do sentido de incidência de e da força eletromotriz induzida na espira durante esse intervalo.
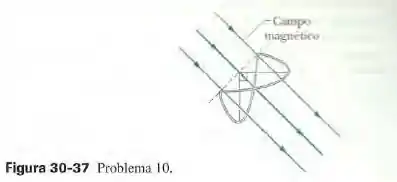
Questão 75
(Capítulo 30.4 – Exercício 15) Uma espira quadrada com de lado é mantida perpendicular a um campo magnético uniforme com metade da área da espira na região em que existe campo, como mostra a figura 30-41. A espira contém uma fonte ideal de força eletromotriz . Se o módulo do campo varia com o tempo de acordo com a equação , com em teslas e em segundos, determine (a) a força eletromotriz total aplicada à espira e (b) o sentido da corrente (total) na espira.
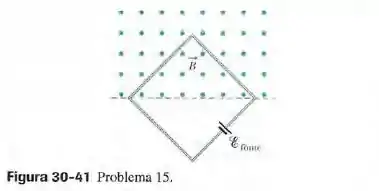
Questão 76
(Capítulo 30.4 – Exercício 26) No sistema da Fig. 30-47, e . A corrente no fio retilíneo longo é dada por , onde está em ampères e em segundos. (a) Determine a força eletromotriz na espira quadrado no instante . (b) Qual o sentido da corrente induzida na espira?
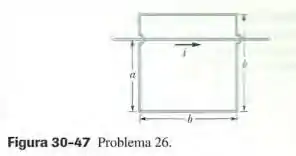
Questão 77
(Capítulo 30.4 – Exercício 21) Na Fig. 30-44, uma semicircunferência de fio de raio gira com uma velocidade angular constante de 40 revoluções por segundo na presença de um campo magnético uniforme . Determine (a) a frequência e (b) a amplitude da força eletromotriz induzida no circuito.
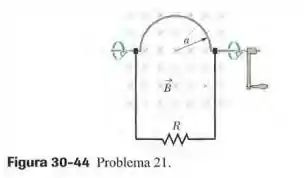
Questão 78
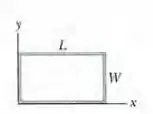
(Capítulo 30.4 – Exercício 12) Na figura 30-39, uma espira retangular de dimensões e é submetida a um campo magnético . Determine (a) o módulo e (b) o sentido (horário ou anti-horário ou “nenhum”, se ) da força eletromotriz induzida na espira se . Determine (c) e (d) o sentido de se Determine (e) e (f) o sentido de se Determine (g) e (h) o sentido de se Determine (i) e (j) o sentido de se
Questão 79
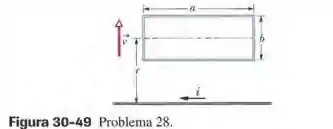
(Capítulo 30.4 – Exercício 28) Na Fig. 30-49, uma espira retangular de comprimento , largura e resistência é colocada nas vizinhanças de um fio infinitamente longo percorrido por uma corrente . Em seguida, a espira é afastada do fio com uma velocidade constante . Quando o centro da espira está a uma distância do fio, determine (a) o valor absoluto do fluxo magnético que atravessa a espira e (b) a corrente induzida na espira.
Questão 80
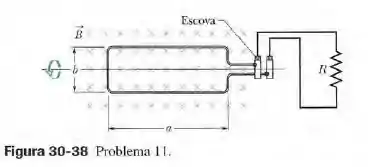
(Capítulo 30.4 – Exercício 11) Uma bobina retangular de comprimento e largura , com espiras, gira com frequência na presença de um campo magnético uniforme , como mostra a figura 30-38. A bobina está ligada a cilindros metálicos que giram solidariamente a ela e nos quais estão apoiadas nas escovas metálicas que fazem contato com um circuito externo. (a) Mostre que a força eletromotriz induzida na bobina é dada (em função do tempo ) pela equação
Este é o princípio de funcionamento dos geradores comerciais de corrente alternada. (b) para que valor de a força eletromotriz gerada tem uma amplitude quando a bobina gira com uma frequência de revoluções por segundo em um campo magnético uniforme de ?
Questão 81
Analise as seguintes afirmativas:
(I) O campo elétrico induzido apresenta linhas fechadas, isso acarreta que o valor de sua circulação seja diferente de zero;
(II) A fem induzida em um circuito é, em módulo, igual à taxa de variação do fluxo magnético através dele;
(III) O sentido da corrente induzida em uma espira é tal que o campo que ela produz se opõe à variação do fluxo magnético que a produziu.
Qual(is) é(são) verdadeira(s)?
(a) Somente a afirmativa (III).
(b) As afirmativas (I) e (II).
(c) As afirmativas (I) e (III).
(d) As afirmativas (II) e (III).
(e) Todas as três afirmativas.
Ver solução completaQuestão 82
A figura abaixo mostra uma espira quadrada de lado que move-se da esquerda para a direita com aceleração constante (). A espira penetra em uma região do espaço em que há um campo magnético constante (), perpendicular ao plano da folha e apontando para dentro. A espira tem resistência . Nessa figura, a variável mede a posição do lado direito da espira com relação à fronteira da região de campo e é uma função do tempo . Suponha que no instante e que a espira parte do repouso.
OBS: Suas respostas devem ser dadas em função apenas de , , e .
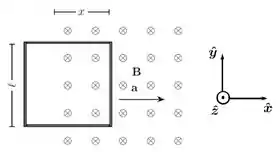
- Determine a intensidade do fluxo de campo magnético através da área definida pela espira como função do tempo , considerando os intervalos em que a espira está entrando no campo e depois que ela está totalmente imersa.
- Determine a intensidade e o sentido da corrente induzida na espira como função do tempo , considerando os mesmos intervalos.
- Faça gráficos da intensidade do fluxo e da corrente induzida como função do tempo , destacando os pontos relevantes.
Questão 83
Indique em ordem, se a frase é falsa (F) ou verdadeira (V).
1 - Existe uma induzida em um fio, que se desloca paralelamente a um campo magnético, se o fio está avançando na direção oposta à do campo magnético.
2 - Um campo magnético constante pode ser usado para produzir uma corrente elétrica.
3 - A em uma barra condutora de comprimento que se move perpendicularmente a um campo magnético é inversamente proporcional à velocidade da barra.
4 - Um fluxo magnético constante através de uma espira condutora induz uma .
5 - De acordo com a Lei de Lenz, o sentido da corrente induzida numa espira condutora sempre gerará um campo magnético na direção oposta ao campo externo aplicado.
a) F V F F F
b) V F F V F
c) F V F V V
d) V F V F F
e) F V V F V
Ver solução completaQuestão 84
Um imã em barra é deixado cair através de uma espira horizontal, como mostra a figura. O polo norte do imã está voltado para baixo e o sul para cima.
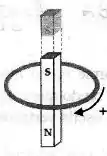
Qual a afirmativa correta?
Não há corrente na espira porque ambas as extremidade do imã passam através da espira.
A corrente na espira é sempre no sentido positivo.
A corrente na espira é sempre no sentido negativo.
A corrente na espira é inicialmente no sentido positivo e depois no sentido negativo.
A corrente na espira é inicialmente no sentido negativo e depois no sentido positivo.
Ver solução completaQuestão 85
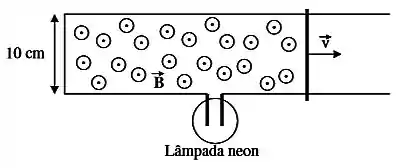
Um fio condutor é dobrado em três partes retilíneas como mostra a figura. Um campo magnético constante e homogêneo de intensidade é aplicado perpendicularmente à área da figura formada. No meio do fio é colocada uma lâmpada Neon, que acende quando a diferença de potencial é de . Uma barra, que pode se mover livremente é colocada entre as duas partes paralelas e é movimenta com velocidade , conforme a figura.
- Ache a velocidade da barra para que a lâmpada acenda.
- Ache o sentido da corrente quando a lâmpada é acesa.
Questão 86
Duas espiras circulares de cobre situam-se sobre o mesmo plano, como mostrado. Uma corrente crescente flui no sentido horário na espira externa. O que acontece na espira interna?
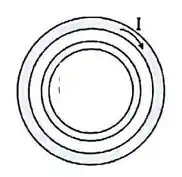
(a) flui uma corrente crescente no sentido horário
(b) flui uma corrente decrescente no sentido horário
(c) flui uma corrente crescente no sentido anti-horário
(d) flui uma corrente decrescente no sentido anti-horário
(e) não flui corrente alguma, pois a espira é interna
Ver solução completaQuestão 87
Um fio longo e reto está no mesmo plano que uma espira retangular, como mostra a figura. O fio conduz uma corrente constante . Qual das seguintes afirmações é verdadeira se o fio se afastar da espira na direção ilustrada na figura?
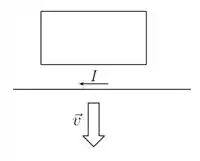
(a) Não haverá fem induzida e nem corrente induzida.
(b) Haverá uma fem induzida, mas nenhuma corrente será induzida.
(c) Haverá uma corrente induzida em torno do circuito, no sentido horário.
(d) Haverá uma corrente induzida em torno do circuito, no sentido anti-horário.
(e) Não haverá campo elétrico induzido.
Ver solução completaQuestão 88
13 - Um fio longo e reto está no plano de uma espira condutora retangular. O fio reto conduz inicialmente uma corrente constante na direção mostrada. No instante em que a corrente é desligada, a corrente induzida na espira:
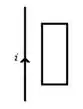
- é zero
- está no sentido horário
- está no sentido anti-horário
- está no sentido horário no lado esquerdo e no sentido anti-horário no lado direito
- está no sentido anti-horário no lado esquerdo e no sentido horário no lado direito
Questão 89
Uma espira condutora circular encontra-se em uma região de campo magnético uniforme, mas não estacionário , que aponta perpendicularmente ao seu plano. A intensidade deste campo varia com o tempo de acordo com o gráfico mostrado abaixo. Os instantes indicados no gráfico são todos positivos e o campo aponta no mesmo sentido durante todo o intervalo indicado. Sobre essa situação, considere as afirmativas abaixo:
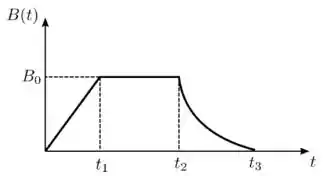
- A corrente induzida na espira durante o intervalo é estacionária.
- Não há corrente induzida na espira durante o intervalo .
- As correntes induzidas na espira durante os intervalos e possuem o mesmo sentido.
São VERDADEIRAS as seguintes afirmativas:
- Nenhuma delas
- e
- e
- , e
- e .
Questão 90
Uma barra metálica horizontal , de comprimento e massa , pode escorregar sem atrito sobre dois trilhos verticais condutores, que estão unidos por uma haste horizontal fixa de resistência . As resistências da barra e do trilho são desprezíveis. O conjunto está em uma região onde há um campo magnético constante (uniforme e estacionário, com ).
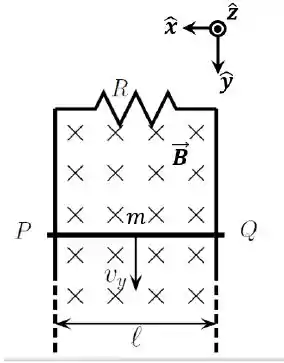
Suponha que, no instante , a barra tenha sido abandonada do repouso e durante seu movimento ela não tenha perdido o contato com os trilhos verticais. Denote por o módulo da aceleração da gravidade ( tem sentido ). Despreze quaisquer efeitos capacitivos ou indutivos no circuito.
Determine o sentido da corrente induzida no circuito.
Calcule a intensidade da corrente induzida no circuito em um instante genérico , em função de , , e . Considere que em a barra ocupava a posição .
Determine a força magnética, , (módulo, direção e sentido) atuando na barra, num instante de tempo , quando a velocidade da mesma tem módulo .
Após algum tempo, a barra entra em movimento uniforme (suponha que esse regime seja atingido antes da barra atingir o solo). Nesse regime, sua velocidade tem módulo (velocidade terminal). Obtenha a expressão para em termos de , , , e .
Ver solução completaQuestão 91
A barra imantada mostrada na figura move-se de modo a atravessar completamente a espira. Qual das seguintes afirmações é verdadeira a respeito do sentido da corrente entre os pontos e do circuito?
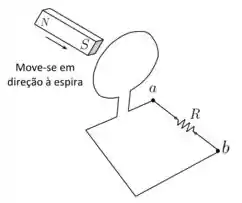
(a) não há corrente entre e enquanto o ímã atravessa a espira.
(b) a corrente flui de para enquanto o ímã entra na espira e de para enquanto o ímã sai da espira.
(c) a corrente flui de para enquanto o ímã entra na espira.
(d) a corrente flui de para enquanto o ímã entra na espira.
(e) a corrente flui de para enquanto o ímã entra na espira e de para enquanto o ímã sai da espira.
Ver solução completaQuestão 92
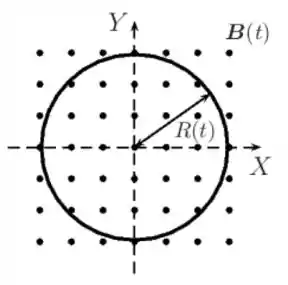
O campo magnético em todos os pontos de uma região cilíndrica de raio é uniforme e direcionado para dentro da página , variando com o tempo segundo , onde é uma constante positiva.
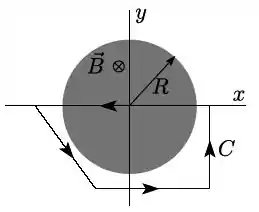
- Determine a integral do campo elétrico ao longo do circuito indicado na figura.
- Determine o vetor campo elétrico fora da região cilíndrica de raio .
- Determine o vetor campo elétrico dentro da região cilíndrica de raio .
Questão 93
O campo magnético no interior de um solenoide ideal de de diâmetro é e está diminuindo a . Quais são as intensidades do campo elétrico no interior do solenoide nos pontos sobre o seu eixo e a do eixo?
e
e
e
e
e
Ver solução completaQuestão 94
Um fio muito longo (que podemos considerar infinito) e paralelo ao eixo está transportando uma corrente variável no tempo . Uma espira quadrada de lados e e resistência total está se deslocando no sentido positivo do eixo com uma velocidade constante . A distância entre o fio e o primeiro segmento da espira é (que também varia no tempo). O sistema está ilustrado na figura abaixo
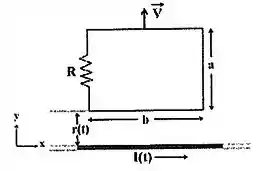
- Encontre a expressão para o fluxo do campo magnético associado à espira.
- Encontre a expressão para da induzida na espira em função da distância e da velocidade .
- Qual é o sentido da corrente induzida na espira?
Suponha agora que a espira para uma distância de do fio (). Neste instante a corrente no fio está aumentando com uma taxa de .
Questão 95
Uma barra condutora se move para a esquerda com velocidade constante apoiada sobre dois trilhos condutores que se juntam do lado esquerdo como mostrada na figura. Como consequência da presença de um campo magnético externo constante e uniforme, uma corrente é induzida na direção indicada. Qual é a direção do campo magnético externo?
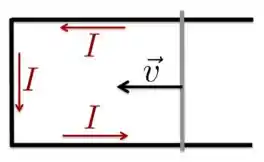
- Para a direita.
- Para a esquerda
- Paralelo à barra condutora.
- Para dentro da página.
- Para fora da página.
Questão 96
Uma bobina retangular com voltas, de lados e e resistência total , está contida no plano e gira com velocidade angular em torno do eixo . Esta bobina é atravessada por um campo magnético de módulo dirigido ao longo do eixo , como mostrado na figura . A rotação é iniciada de modo que o plano da bobina seja perpendicular à direção de em .
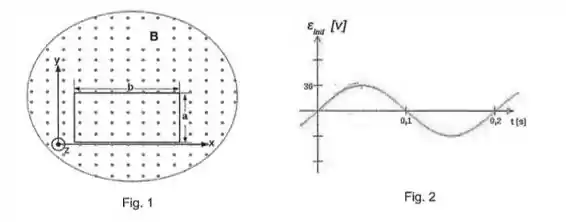
A figura mostra o comportamento da tensão induzida na bobina em função do tempo. Utilizando a figura e os outros dados do problema, encontre:
(a) O número de voltas da bobina retangular;
(b) A taxa máxima de variação do fluxo magnético através da bobina;
(c) O valor da corrente induzida e seu sentido (horário ou anti-horário) na bobina quando ;
(d) A potência média dissipada no resistor.
(Sugestão: em todos os cálculos use )
Ver solução completaQuestão 97
Considere um anel circular condutor, situado no plano e centrado na origem, imerso em um campo magnético uniforme , como mostrado na figura abaixo. O anel então é aquecido, de modo que o seu raio varia no tempo como , onde e são constantes positivas. Além disso, o campo magnético também varia no tempo como , onde também é uma constante positiva.
- Determine o fluxo magnético através da área definida pelo anel em um instante .
- Determine a intensidade e o sentido da força eletromotriz induzida no anel no mesmo instante.