Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 10.Problemas - Ex. 8
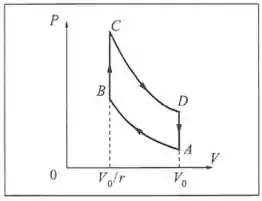
A figura abaixo, onde e são adiabáticas, representa o ciclo de Otto, esquematização idealizada do que ocorre num motor a gasolina de tempos: representa a compressão rápida (adiabática) da mistura de ar com vapor de gasolina, de um volume inicial para ( taxa de compressão); representa o aquecimento a volume constante devido à ignição; é a expansão adiabática dos gases aquecidos, movendo o pistão; simboliza a queda de pressão associada à exaustão dos gases da combustão. A mistura é tratada como um gás ideal de coeficiente adiabático . (a) Mostre que o rendimento do ciclo é dad por
(b) Calcule para e (compressao máxima permissível para evitar pré-ignição).
Passo 1
(a) Vamos começar lembrando da fórmula para o rendimento:
Então beleza, precisamos calcular o trabalho realizado e o calor absorvido ao longo de cada ciclo.
Pra isso vamos precisar dessa fórmula aqui:
Que pela lei dos gases ideias, é a mesma coisa que:
O trabalho só não é nulo em dois trechos: e , e aí é só substituir na fórmula:
Ou seja, o trabalho total é:
Passo 2
E agora temos que calcular o calor absorvido em cada ciclo. Lembrando que e são adiabáticos, ou seja, não temos troca de calor.
No trecho a temperatura está diminuindo, então o calor só é absorvido no outro trecho, que é .
Pela primeira lei da termodinâmica:
E já que o volume é constante nesse processo, o trabalho é nulo:
E agora vamos usar a fórmula para a variação de energia interna:
Dá pra escrever em função de usando essa fórmula aqui:
Então:
Agora podemos voltar na fórmula do rendimento :
Organizando um pouco:
E agora chegamos na fórmula que aparece no enunciado:
Passo 3
Agora fica faltando a segunda parte da igualdade:
Pra demonstrar isso, vamos começar olhando para os dois processos adiabáticos: e .
E agora vamos usar a lei dos gases ideais em cada um dos pontos:
Substituindo os volumes de acordo com o gráfico:
E substituindo as pressões e usando a conta que ali de cima:
Agora vamos tentar usar esse sistema pra demonstrar a equação que aparece no enunciado.
Passo 4
Primeiro subtraímos a primeira equação da última, pra encontrar a diferença de temperaturas :
E então fazemos a mesma coisa com a terceira e a segunda equações pra encontrar
E então, pra voltar na fórmula do enunciado, vamos fazer a razão entre essas duas diferenças de temperaturas:
E pela fórmula que demonstramos no passo de cima:
Pronto! Conseguimos demonstrar a fórmula do item (a).
Passo 5
(b) Agora é só substituir os valore numéricos para calcular :
Como e :
Resposta
(a) Demonstração.
(b) .