Exercícios de Máquinas Térmicas e Refrigeradores - Lista de Exercícios Resolvida
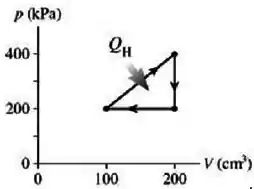
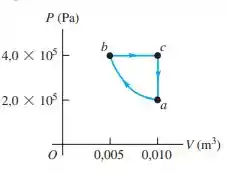
Questão 1
Quais são e , e o rendimento térmico da máquina térmica mostrada na figura?
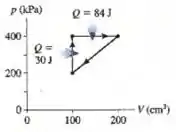
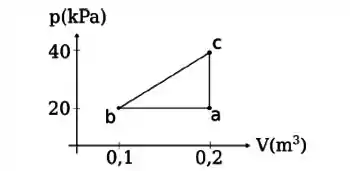
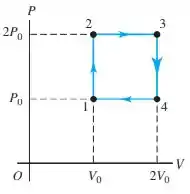
Questão 2
Um gás ideal é a substância de trabalho em uma máquina térmica que descreve o ciclo mostrado na figura abaixo. Os processos e são reversíveis e adiabáticos. O gás é monoatômico, diatômico ou poliatômico? Qual é a eficiencia da máquina?
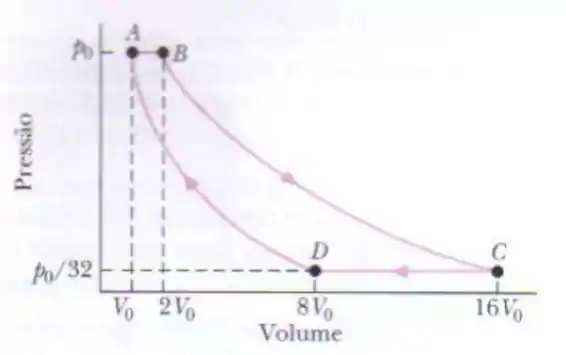
Questão 3
A figura mostra o ciclo de uma máquina térmica que usa gás com . A temperatura inicial é , e a máquina opera a ciclos por segundo.
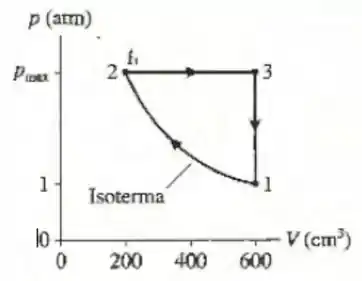
Qual é a potência de saída da máquina?
Qual é o rendimento térmico da máquina?
Ver solução completaQuestão 4
Um refrigerador ideal realiza de trabalho para remover em forma de calor do compartimento frio. Qual é o coeficiente de desempenho do refrigerador? Qual é a quantidade de energia em forma de calor liberada para a cozinha por ciclo?
Ver solução completaQuestão 5
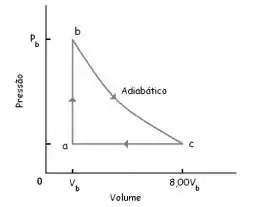
A figura mostra um ciclo reversível percorrido por de um gás monoatômico ideal. O processo é uma expansão adiabática, com e. Para este ciclo, encontre:
A energia adicionada ao gás na forma de calor.
A energia liberada pelo gás na forma de calor.
O trabalho líquido realizado pelo gás
A eficiência do ciclo
Dados:
- gás monoatômico: , e
- pressão atmosférica
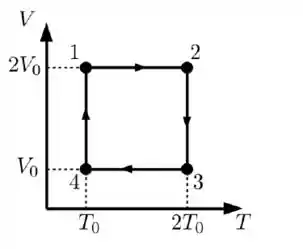
Questão 6
Um mol de gás ideal monoatômico é submetido ao ciclo mostrado na figura.
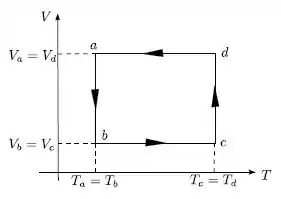
Desenhe o ciclo correspondente no plano (P.V) especificando o tipo de cada etapa.
Calcule o trabalho realizado (ou sofrido) pelo gás em cada etapa, em termos dos dados da figura e da constante universal dos gases .
Calcule o calor absorvido (ou cedido) pelo gás em cada etapa, em termos dos dados da figura e da constante universal dos gases .
Este ciclo corresponde a um motor ou a um refrigerador? Por quê?
Ver solução completaQuestão 7
Três mols de um gás ideal monoatômico passam pelo ciclo termodinâmico descrito na figura( isobárico, isotérmico e isocórico):
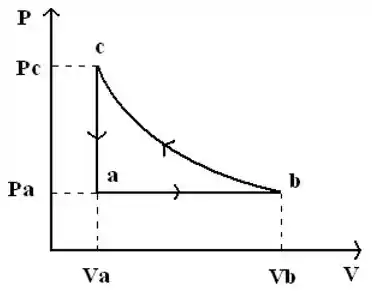
Dados , e , determine , e (tome e trabalhe com dois algarismos significativos).
Determine o trabalho realizado pelo sistema , o calor cedido ao sistema e a variação da energia interna para cada processo e preencha a tabela (justifique cada valor encontrado):

O ciclo considerado descreve uma máquina térmica ou um refrigerador? Justifique
Calcule a eficiência (se for máquina), ou coeficiente de desempenho (se for refrigerador), do ciclo.
Faça um gráfico do ciclo considerado.
Ver solução completaQuestão 8
Em uma máquina de Stirling idealizada o fluido de trabalho (considerado um gás ideal) realiza as seguintes etapas reversíveis:
: Uma expansão isotérmica do volume ao volume à temperatura .: Um resfriamento a volume constante, atingindo a temperatura .: Uma compressão isotérmica à temperatura , reduzindo o volume de a : Um aquecimento a volume constante, de forma que o gás retorne ao seu estado inicial.
Expresse suas respostas em termos de , , e , da constante dos gases , do calor específico molar a volume constante e do número de moles do fluido.
Esquematize o diagrama PV para este ciclo.
Calcule o trabalho realizado em cada etapa deste ciclo.
Calcule o calor transferido em cada etapa deste ciclo.
A eficiência da máquina.
Ver solução completaQuestão 9
Uma amostra de um gás ideal () passa pelo processo mostrado na figura abaixo.
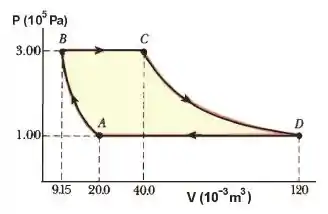
De a , o processo é adiabático. De a é isobárico com de energia entrando no sistema por calor. De a , o processo é isotérmico. De a , é isobárico com de energia saindo do sistema por calor.
- Encontre as temperaturas dos estados , e do processo isotérmico.
- Responda, justificando, se o gás é mono-, di- ou poliatômico.
- Reproduza a tabela abaixo no caderno de respostas. Complete-a, justificando, com os valores de , e para cada um dos processos e para o ciclo.
- Calcule a eficiência de uma máquina que funcione com esse ciclo.

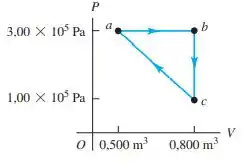
Questão 10
Uma amostra de gás Hélio está incialmente à pressão , volume ( 1 litro) e temperatura O gás é expandido isotermicamente até seu volume atingir . Em seguida, é comprimido à pressão constante até determinado volume e retorna ao seu estado inicial após uma compressão adiabática.
- Faça um esquema desse ciclo em um diagrama (pressão x volume).
- Encontre o valor de para o gás hélio e obtenha o valor de para essa amostra (coloque unidades).
- Calcule o volume e a temperatura após a compressão isobárica.
- Calcule o trabalho realizado no ciclo.
- Calcule o rendimento da máquina que trabalha segundo esse ciclo.
Dados:
Ver solução completaQuestão 11
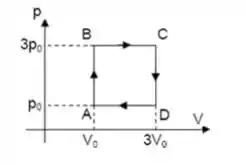
Uma máquina térmica funciona de modo que mols de um gás ideal monoatômico descrevem o processo ciclíco representado no diagrama ao lado. Sabendo que o calor absorvido pela máquina em cada ciclo é , qual é o rendimento da máquina?
Questão 12
A respeito de máquinas térmicas e refrigeradores assinale a alternativa INCORRETA.
- Em um refrigerador sempre se joga mais calor na fonte quente do que se retirou da fria.
- Um refrigerador perfeito (no qual o trabalho realizado é zero) pode ser pensado como uma máquina perfeita (para a qual a eficiência é de ) operando reversamente.
- Pela segunda lei da termodinâmica podemos afirmar que não existem nem refrigeradores perfeitos nem máquinas perfeitas.
- Quanto maior a diferença entre as temperaturas da fonte fria e da fonte quente tanto maior é a eficiência que uma máquina térmica pode ter.
Questão 13
O gráfico ao lado mostra o ciclo de uma máquina térmica para o qual . Qual é a eficiência térmica desta máquina?
A) 57 %
B) 29 %
C) 14 %
D) 23 %
E)20 %
Ver solução completaQuestão 14
Qual o rendimento da máquina térmica que realiza o ciclo da figura abaixo? Considere .
- .
- .
- Não se pode calculá-lo sem saber o calor rejeitado para o reservatório Frio.
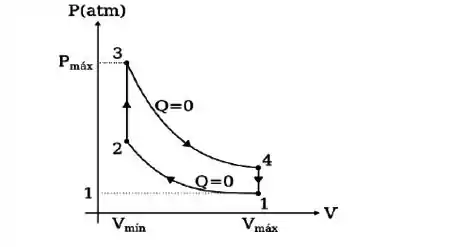
Questão 15
O funcionamento do motor a gasolina de seu carro pode ser tratado pelo modelo do Ciclo de Otto representado na figura abaixo. Neste motor, é o fator de compressão:
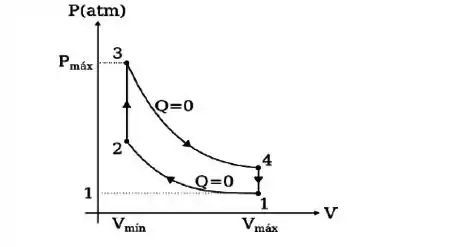
Usando as relações adiabáticas entre e , pode-se mostrar que o rendimento vale:
Questão 16
O funcionamento do motor a gasolina de seu carro pode ser tratado pelo modelo do Ciclo de Otto representado na figura abaixo. Neste motor, é o fator de compressão:
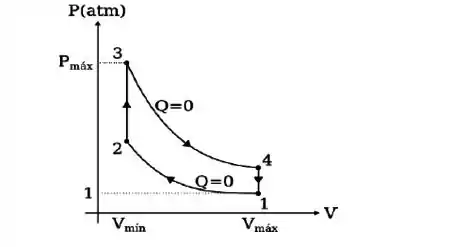
O trabalho útil do Ciclo de Otto em cada ciclo vale:
Questão 17
Considere pontos no diagrama com as seguintes pressões e volumes. Ponto A:
(2,); Ponto B: (,2); Ponto C: (,2); Ponto D: (,). Considere que de um gás ideal sejam colocados para realizar os seguintes ciclos:
Ciclo : o gás passa por uma expansão isobárica do ponto A até o ponto B e depois por um processo isocórico do ponto B para o ponto C. Em seguida, é comprimido isobaricamente do ponto C para o ponto D e finalmente retorna isocoricamente ao ponto A.
Ciclo : o gás passa por uma expansão isobárica do ponto A até o ponto B, e depois por um processo isocórico do ponto B para o ponto C. Finalmente, o gás e comprimido isotermicamente do ponto C para o ponto A.
Com relação a estes dois ciclos e , podemos afirmar que:
- Ambos podem representar o funcionamento de uma maquina térmica.
- Ambos podem representar o funcionamento de um refrigerador.
- O ciclo pode representar uma maquina termica e o ciclo um refrigerador.
- O ciclo pode representar um refrigerador e o ciclo uma maquina térmica.
- No ciclo seria possivel trocar o processo isotérmico por um processo adiabático.
Questão 18
Considere pontos no diagrama com as seguintes pressões e volumes. Ponto A:
(2,); Ponto B: (,2); Ponto C: (,2); Ponto D: (,). Considere que de um gás ideal sejam colocados para realizar os seguintes ciclos:
Ciclo : o gás passa por uma expansão isobárica do ponto A até o ponto B, e depois por um processo isocórico do ponto B para o ponto C. Em seguida, é comprimido isobaricamente do ponto C para o ponto D e finalmente retorna isocoricamente ao ponto A.
Ciclo : o gás passa por uma expansão isobárica do ponto A ate o ponto B, e depois por um processo isocórico do ponto B para o ponto C. Finalmente, o gás é comprimido isotermicamente do ponto C para o ponto A.
Ainda considerando os ciclos e , assinale a opção CORRETA:
- O rendimento tanto do ciclo quanto do ciclo depende do numero de mols n do gás.
- O rendimento tanto o ciclo quanto do ciclo não dependem do tipo de gás (monoatômico ou diatômico).
- O rendimento tanto o ciclo quanto do ciclo dependem dos valores e .
- Independente do tipo de gás (monoatômico ou diatômico), o rendimento de e maior que a de .
- Independente do tipo de gás (monoatômico ou diatômico), o rendimento de e menor que a de .
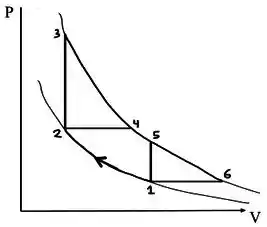
Questão 19
Um gás ideal inicialmente num estado em equilíbrio térmico sofre três processos termodinâmicos, executando o ciclo , como descrito pela figura abaixo. Podemos afirmar que:
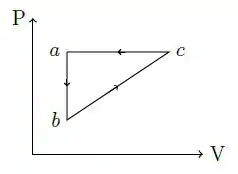
I – Estes processos combinados descrevem um refrigerador
II – O calor total recebido pelo sistema é positivo,
III – A energia interna do gás em é menor que em
IV – Em módulo, o trabalho total envolvido nestes processos é dado pela área interna à curva
Destas afirmações, as corretas são:
(a) I, II e IV
(b) I e IV
(c) II, III e IV
(d) I e II
Ver solução completaQuestão 20
Você e seu colega de quarto precisam de um novo refrigerador. Na loja de eletrodomésticos, o vendedor mostra a vocês a “geladeira dos sonhos”. De acordo com a etiqueta do fabricante, essa geladeira utiliza meros de potência para retirar de calor por minuto de seu interior a e rejeitar de calor por minuto para a cozinha. De acordo com o texto em letras miúdas na etiqueta, isto é verdadeiro apenas para uma cozinha que esteja a . Você deveria comprá-la?
- Não, pois essa geladeira viola tanto a primeira como a segunda leis da termodinâmica.
- Não, pois essa geladeira viola a primeira lei mas não a segunda lei da termodinâmica.
- Não, pois essa geladeira não viola a primeira lei mas viola a segunda lei da termodinâmica.
- Sim, pois essa geladeira não viola nem a primeira lei nem a segunda lei da termodinâmica.
- Sim, pois a “geladeira dos sonhos” funciona tão bem como um ciclo de Carnot.
Questão 21
Uma máquina térmica que usa de hélio gasoso (monoatômico) encontra-se inicialmente a uma temperatura de , a uma pressão de . O gás descreve o seguinte ciclo fechado:
- Uma compressão isotérmica até que o volume se reduza à metade e a pressão dobre.
- Uma expansão isobárica até que o volume seja restaurado ao valor inicial.
- Um resfriamento isocórico até que a pressão seja restaurada ao valor inicial.
Qual é, aproximadamente, o trabalho que a máquina realiza a cada ciclo e seu rendimento térmico?
Questão 22
Qual é a máxima eficiência teórica possível para um refrigerador operando entre um reservatório no qual coexistem gelo e água e um reservatório em que coexistem água e vapor? A pressão é constante em 1,0 atm para ambos os reservatórios.
- 2,7
- 4,5
- 7,3
- 1,7
- 5,4
Questão 23
Uma dada quantidade de calor é absorvida por uma máquina térmica a partir de um forno a uma taxa de . Se o calor que a máquina rejeita é absorvido por um rio a uma taxa de , a eficiência térmica da máquina é:
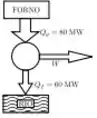
(a)
(b)
(c)
(d) Nenhuma das respostas.
Ver solução completaQuestão 24
Uma máquina térmica opera entre e . Em cada ciclo ela extrai do reservatório quente, rejeita no reservatório frio, e realiza de trabalho. Esta máquina viola:
- tanto a primeira lei como a segunda lei da termodinâmica.
- a primeira lei mas não a segunda lei da termodinâmica.
- a segunda lei mas não a primeira lei da termodinâmica.
- nem a primeira lei nem a segunda lei da termodinâmica.
- não pode ser respondida sem saber o calor resultante da máquina.
Questão 25
Assinale a opção CORRETA :
- um refrigerador é um dispositivo que transfere calor espontaneamente de um reservatório frio para um quente
- um refrigerador pode operar em um ciclo aberto
- um refrigerador opera em ciclo fechado, admite calor de um reservatório frio através da realização de trabalho e transfere parte deste calor ao reservatório quente
- um refrigerador opera em ciclo fechado, admite calor de um reservatório frio e o transfere integralmente ao reservatório quente
- um refrigerador trabalha retirando calor de um reservatório frio, fornecendo trabalho útil e rejeitando calor no reservatório quente
Questão 26
Uma amostra com de um gás ideal diatômico, , é submetida a um processo cíclico, Inicialmente, , o gás ocupa um volume de à temperatura de e então é comprimido adiabaticamente até atingir o volume de , ponto . Em seguida, o gás é aquecido a pressão constante até retornar ao volume inicial, . Finalmente o gás retorna ao ponto em um processo no qual o volume é mantido constante.
Determine os valores de pressão, volume e temperatura remanescentes nos pontos completando a tabela a seguir.
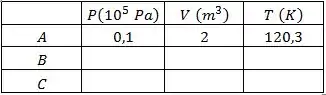
Faça um esboço do processo no plano .
Preencha a tabela com os valores determinados para o calor trocado e o trabalho realizado em cada trecho do processo cíclico, tomando os sinais positivos como os correspondentes a calor recebido e a trabalho realizado pelo gás e negativos em casos opostos.
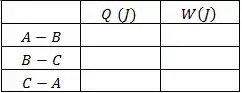
Qual é a eficiência de uma máquina térmica que opere com esse processo cíclico?
Ver solução completaQuestão 27
A figura abaixo mostra um cilindro contendo um mol do gás nitrogênio (), fechado por um pistão móvel e submerso numa mistura de gelo com água (). O gás sofre as seguintes transformações (diagrama ao lado da figura):
(1) O pistão, inicialmente na posição , é empurrado rapidamente para baixo, até a posição (processo adiabático), comprimindo o gás até ;(2) É, então, mantido na posição até que o gás esteja novamente na temperatura da mistura gelo-água (considere este processo como reversível isovolumétrico).(3) Em seguida, o pistão é erguido lentamente de volta à posição (processo isotérmico).
Observa-se que de gelo são derretidos durante o ciclo. (Calor de fusão do gelo ).
Dados:
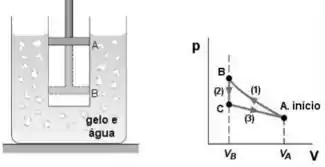
Tabela:

- Calcule o calor trocado entre o gás e a mistura gelo-água durante o ciclo. Obtenha o trabalho realizado sobre o gás durante o ciclo e complete a última linha da tabela acima.
- Calcule o trabalho realizado pelo gás na etapa (3) e complete, na tabela, a linha correspondente a essa etapa.
- Obtenha o trabalho realizado sobre o gás na etapa (2) e coloque o valor na tabela. Em seguida, calcule o trabalho na etapa (1) e complete a linha (1) da tabela.
- Calcule o calor cedido pelo gás na etapa (2) e Complete a linha (2) da tabela.
Questão 28
Uma amostra com moles de um gás ideal cujo calor específico molar a volume constante vale realiza o ciclo ilustrado no diagrama abaixo.
a) Faça um esboço do ciclo acima em um diagrama , indicando os estados , bem como a pressão e o volume de cada estado em função de e .
b) Determine o calor envolvido em cada etapa do ciclo.
c) Determine o trabalho total realizado no ciclo.
d) Este ciclo representa uma máquina térmica ou refrigerador?
Justifique a sua resposta.
Ver solução completaQuestão 29
(Cap 20 – Prob 49) Um gás monoatomico ideal executa o ciclo da Figura 20.29 no sentido indicado na figura. O caminho do processo é uma linda reta no diagrama . a) Calcule e em cada processo: , e . b) Quais são os volume de e em um ciclo completo? c) Qual é a eficiencia do ciclo?
Questão 30
Um refrigerador trabalha entre as temperaturas e tem um quarto do coeficiente de rendimento máximo para essas dadas temperaturas. Se a taxa com que ele recebe o trabalho é de 60W, quanto calor ele absorve do ambiente mais frio em um minuto?
Escolha uma opção:
- 42000J
- 6300J
- 3600J
- 10500J
- 25200J
Questão 31
O funcionamento do motor a gasolina de seu carro pode ser tratado pelo modelo do Ciclo de Otto representado na figura abaixo. Neste motor, é o fator de compressão:
No caso dos reservatórios térmicos desse motor, podemos afirmar que:
Questão 32
(Cap 20 – Ex 5) Certa usina termelétrica alimentada por reação nuclear produz uma potência mecânica (usada para operar um gerador elétrico igual a . Sua taxa de absorção de calor do reator é igual a . a) Qual é a eficiência térmica? b) Com que taxa o calor é rejeitado?
Ver solução completaQuestão 33
(Cap 20 – Ex 12) Um freezer possui coeficiente de desempenho igual a . O freezer deve converter de água a em de gelo a em uma hora. a) Que quantidade de calor deve ser removida da água a para convertê-la em gelo a ? b) Qual é a energia elétrica consumida pelo freezer durante uma hora? c) Qual é a quantidade de calor rejeitado para a sala na qual o freezer está localizado?
Ver solução completaQuestão 34
(Cap 20 – Ex 1) Um motor Diesel produz de trabalho mecânico e rejeita de calor em cada ciclo. a) Qual deve ser a quantidade de calor a ser fornecida para a máquina em cada ciclo? b) Qual é a eficiência térmica da máquina?
Ver solução completaQuestão 35
Uma máquina térmica usa 0,02 mol de um gás diatômico como substância de trabalho. Ela é descrita pelo ciclo mostrado na figura ao lado, onde o processo de 1 para 2 é adiabático.
Qual o rendimento térmico da máquina?
Dados: , , , .
a) 75 %
b) 15%
c) 17%
d) 21%
e) 34 %
Ver solução completaQuestão 36
Qual é o máximo coeficiente de desempenho de um refrigerador de Carnot operando em uma sala à temperatura de , se a temperatura no interior do refrigerador é mantida a ?
- 13,8;
- 0,1;
- 0,44;
- 5,8;
- 3,0;
Questão 37
A temperatura do reservatório frio de uma máquina térmica reversível com um rendimento de é . Em cada ciclo a máquina entrega ao reservatório frio. Quanto calor é cedido pelo reservatório quente, em kcal?
Questão 38
Um mol de gás ideal, com calor específico molar a volume constante , é submetido à seguinte sequência de processos REVERSÍVEIS:
• Compressão adiabática do estado inicial para o estado;
• Expansão isobárica do estado ao estado ;
• Expansão adiabática do estado ao estado ;
• Diminuição de pressão, a volume constante, do estado ao estado .
1. Desenhe o diagrama PV do ciclo ESPECIFICANDO AS CURVAS CORRESPONDENTES A CADA ETAPA E A ORIENTAÇÃO DO CICLO.
2. Calcule o calor trocado (INDICANDO SE FOI ABSORVIDO OU CEDIDO) pelo sistema em cada etapa em termos das temperaturas nos estados , , e , de e, se necessário, da constante universal dos gases.
3. Calcule o trabalho realizado pelo sistema em cada etapa, em termos das mesmas variáveis.
4. Este ciclo descreve um motor ou um refrigerador? Calcule o rendimento, caso seja um motor, ou o coeficiente de desempenho , caso seja um refrigerador, em termos das mesmas quantidades do item anterior.
Ver solução completaQuestão 39
(Cap 20 – Prob 41) Você constrói uma máquina térmica que requer de um gás ideal diatômico em todo o ciclo mostrado na figura 20.25. a) Mostre que o segmento é uma compressão isotérmica. b) Durant qual(is) segmento(s) do ciclo o calor é absorvido pelo gás? Durante qual(is) segmento(s) o calor é rejeitado? Como você sabe disso? c) Calcule a temperatura nos pontos , e . d) Calcule o calor total trocado com o meio ambiente e o trabalho realizado pela máquina em um ciclo. Calcule a eficiência térmica da máquina.
Questão 40
(Cap 20 – Prob 46) Calcule a eficiência térmica da máquina que usa moles de um gas ideal diatômico e executa o ciclo mostrado na Figura 20.27.
Questão 41
Se o coeficiente de desempenho de um refrigerador é de de trabalho são feitos no sistema, quanto calor é aproximadamente rejeitado para a sala?
Questão 42
(Cap 20 – Ex 3) Um motor a gasolina consome de calor e realiza de trabalho em cada ciclo. O calor é obtido pela queima de gasolina com calor de combustão igual a . a) Qual é a eficiência térmica? b) Qual é a quantidade de calor rejeitada em cada ciclo? c) Qual é a massa de combustível queimado em cada ciclo? d) Se o motor gira com ciclos por segundo, qual é a potencia fornecida pelo motor em quilowatts?
Ver solução completaQuestão 43
A respeito de máquinas térmicas e refrigeradores assinale a alternativa INCORRETA.
(a) Em um refrigerador sempre se joga mais calor na fonte quente do que se retirou da fria.
(b) Um refrigerador perfeito (no qual o trabalho realizado é zero) pode ser pensado como uma máquina perfeita (para a qual a eficiência é de 100%) operando reversamente.
(c) Pela segunda lei da termodinâmica podemos afirmar que não existem nem refrigeradores perfeitos nem máquinas perfeitas.
(d) Quanto maior a diferença entre as temperaturas da fonte fria e da fonte quente tanto maior é a eficiência que uma máquina térmica pode ter.
Ver solução completaQuestão 44
Um motor, quando não está devidamente lubrificado, possui um rendimento , cedendo uma certa quantidade de calor ao reservatório frio quando em funcionamento. Quando corretamente lubrificado, seu rendimento aumenta em Nessas condições, para uma mesma quantidade de calor recebida, a nova quantidade de calor cedida pelo motor será
Questão 45
A figura mostra duas curvas adiabáticas em um diagrama PV de um gás ideal.
É possível construir diferentes máquinas térmicas que envolvam compressões e expansões adiabáticas do gás ao longo dessas mesmas duas curvas. Por exemplo, o mesmo trecho de compressão adiabática pode ser incluído em um chamado ciclo de Brayton (composto de dois trechos adiabáticos e dois trechos isobáricos) e num chamado ciclo de Otto (composto de dois trechos adibáticos e dois isovolumétricos). Os rendimentos destes ciclos são dados respectivamente pelas expressões:
Onde e são as razões entre a máxima e mínima pressão (resp. , volume) atingidos ao longo de cada ciclo respectivo.
Comparando as eficiências dos ciclos de Brayton e de Otto contendo o trecho 1-2 na figura acima, podemos concluir que
A)
B)
C)
D) pode ser , ou que , dependendo do valor da pressão no ponto 1
E) pode ser ou que , dependendo do valor de
Ver solução completaQuestão 46
Uma máquina térmica funciona com um gás ideal diatômico segundo um ciclo de Diesel( diagrama pV mostrado na figura abaixo, onde as transformações são adiabáticas). Considere que a pressão, o volume a temperatura do gás em são , respectivamente.
Considere e
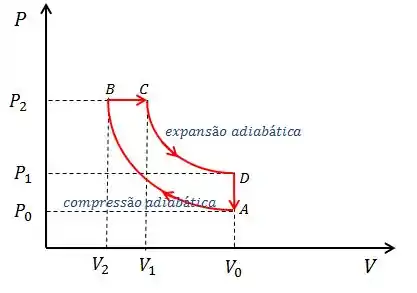
- Encontre as pressões , em função de
- Determine as temperaturas do gás nos estados respectivamente em função de
- Obtenha em função de , o calor trocado entre o gás e as vizinhanças nos processos Diga qual foi o sentido da troca de calor em cada processo.
- Calcule, em função de , o trabalho total realizado pelo ciclo.
- Obtenha o rendimento da máquina que opera segundo esse ciclo.
Questão 47
A máxima eficiência teórica de uma máquina térmica que opera no ciclo de Carnot entre uma fonte quente à temperatura de ebulição da água e uma fonte fria à temperatura ambiente () é, aproximadamente:
Escolha uma:
- 80%;
- 10%;
- 50%;
- 99%;
- 20%;
Questão 48
Um mol de gás ideal monoatômico é submetido ao ciclo mostrado na figura.
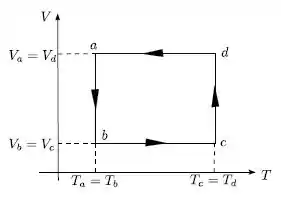
- Desenhe o ciclo correspondente no plano (P.V) especificando o tipo de cada etapa.
- Calcule o trabalho realizado (ou sofrido) pelo gás em cada etapa, em termos dos dados da figura e da constante universal dos gases .
- Calcule o calor absorvido (ou cedido) pelo gás em cada etapa, em termos dos dados da figura e da constante universal dos gases .
- Este ciclo corresponde a um motor ou a um refrigerador? Por quê?
Questão 49
Um youtuber diz ter inventado 4 máquinas. Todas operam entre os mesmos 2 reservatórios de calor, a e a . O calor trocado por cada máquina com o reservatório a temperatura alta () e com o reservatório a temperatura baixa () e o trabalho realizado () por cada máquina em um ciclo são:
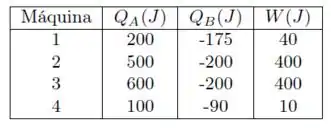
Considere as seguintes afirmações sobre a violação da Primeira e da Segunda Leis da Termodinâmica:
(I) Apenas as máquinas 1 e 2 violam a 1ª Lei.
(II) Apenas as máquinas 2 e 3 violam a 2ª Lei.
(III) Apenas a máquina 2 viola a 2ª Lei.
(IV) Apenas a máquina 4 viola a 2ª Lei.
(V) Apenas a máquina 3 é viável.
Estão corretas:
(a) Apenas as afirmativas I e II.
(b) Apenas as afirmativas I e V.
(c) Apenas as afirmativas IV e V.
(d) Apenas as afirmativas I e III.
Ver solução completaQuestão 50
6 - Um ar condicionado de Carnot opera entre dentro de um ambiente e do lado de fora. Quanto trabalho o compressor precisa fazer para retirar do interior num ciclo completo?
Questão 51
A máquina térmica no diagrama ao lado poderia ser realizada fisicamente?
Dados:
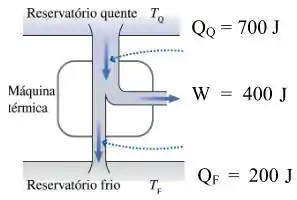
a) Sim, pois ela respeita a 1a e 2a leis da termodinâmica
b) Não, pois ela respeita a 1a e 2a leis da termodinâmica
c) Não, pois ela respeita a 1a lei da termodinâmica mas viola a 2a lei.
d) Não, pois ela respeita a 2a lei da termodinâmica mas viola a 1ª lei.
e) Não, pois ela viola a 1a e 2a leis da termodinâmica
Ver solução completaQuestão 52
Qual das seguintes afirmações é correta?
- Operando num ciclo, uma máquina térmica absorve calor de um reservatório quente, realiza trabalho e rejeita igual quantidade de calor para um reservatório frio a temperatura mais baixa.
- Operando num ciclo, uma máquina térmica absorve calor de um reservatório quente, realiza trabalho e rejeita parte do calor para um reservatório frio a temperatura mais baixa.
- Operando num ciclo, uma máquina térmica retira calor de um reservatório frio, realiza trabalho e rejeita parte do calor para um reservatório quente a temperatura mais alta.
- Operando num ciclo, uma máquina térmica consome trabalho para transferir calor de um reservatório quente para um reservatório frio a temperatura mais baixa.
- Operando num ciclo, um refrigerante consome trabalho para retirar calor de um reservatório frio e transferir a mesma quantidade de calor para um reservatório quente a temperatura mais alta.
Questão 53
Um aquecedor extrai J por hora do meio ambiente a 270 K para manter o interior de uma casa à temperatura de 300 K. Qual é a quantidade mínima de energia elétrica por hora que deve ser fornecida ao aquecedor para que ele possa funcionar?
Ver solução completaQuestão 54
Para a máquina térmica ilustrada abaixo, calcule:
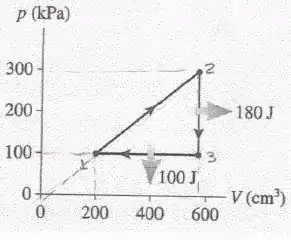
- O rendimento térmico.
- E o calor extraído do reservatório quente.
Questão 55
A eficiência de uma máquina térmica que opera entre uma fonte quente à temperatura e uma fonte fria à temperatura é dada por
- Quaisquer que sejam as características da máquina;
- Apenas se a máquina for quase-estática;
- Apenas se o fluido de trabalho for um gás ideal;
- Apenas se a máquina for reversível;
- Apenas se a máquina operar no ciclo de Stirling.
Questão 56
Um mol de um gás monoatômico ideal é utilizado como substância de trabalho de uma máquina térmica que opera de acordo com o ciclo mostrado no diagrama da figura. Suponha que e . A etapa corresponde a um processo irreversível em que o trabalho realizado vale
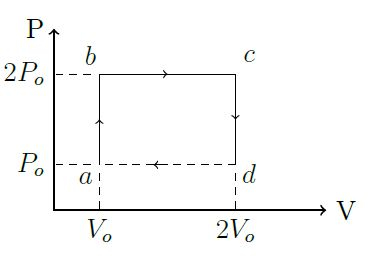
(a) Determine as temperaturas nos pontos , , e
(b) Determine o calor , o trabalho e a variação de energia interna em cada etapa deste ciclo
(c) Calcule a eficiência desta máquina térmica
(d) Determine a variação de entropia em cada etapa deste ciclo.
Ver solução completaQuestão 57
4) Rendimento de uma máquina térmica.
Uma certa quantidade de gás ideal é submetida ao ciclo indicado no diagrama da figura. O calor rejeitado na etapa vale . O calor transferido na etapa vale:
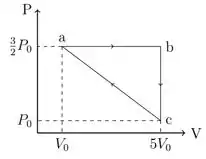
1.
2.
3.
4.
5.
6.
Ver solução completaQuestão 58
substância de trabalho de uma máquina térmica opera no ciclo mostrado no diagrama pressão-volume abaixo. Considere que a substancia de trabalho se comporta como um gás ideal monoatômico.
- (1,0) Calcule, em termos de p0 e , o trabalho realizado pela substância em cada um dos processos .
- (1,5) Determine, em termos de , a energia transferida para a substância sob forma de calor em cada um dos processos .
- (1,0) Calcule a eficiência " da máquina térmica operando no ciclo .
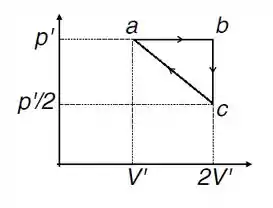
Questão 59
Uma máquia térmica opera com um gás ideal segundo o ciclo representado no diagrama PV ao lado. Qual das afirmações abaixo é correta?
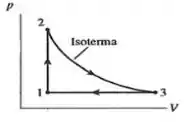
- O gás recebe calor no estágio 1 2 e cede calor nos estágios 2 3 e 3 1.
- O gás recebe calor nos estágios 1 2 e 2 3 e cede calor no estágio 3 1.
- O gás recebe calor no estágio 1 2, cede calor no estágio 3 1 e não há troca de calor no estágio 2 3
- O gás recebe calor no estágio 2 3 e cede calor nos estágios 1 2 e 3 1
- O gás cede calor no estágio 1 2 e recebe calor nos estágios 2 3 e 3 1