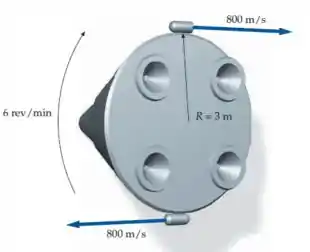
A figura mostra uma visão posterior de uma cápsula espacial que ficou girando rapidamente em torno de seu eixo, a , após uma colisão com outra cápsula. Você é o controlador de voo e tem pouco tempo para instruir a tripulação sobre como parar essa rotação antes que todos fiquem enjoados devido à rotação e a situação se torne perigosa. Você sabe que eles têm acesso a dois pequenos jatos montados tangencialmente a uma distância a partir do eixo, como indicado na figura. Estes jatos podem ejetar, cada um de gás, com uma rapidez de . Determine o intervalo de tempo em que estes jatos devem funcionar para parar a rotação. Em voo, o momento de inércia (suposto constante) da cápsula em relação ao seu eixo vale .

Cada um dos jatos produz uma força e está a uma distância perpendicular de em relação ao eixo, portanto o torque gerado por eles é:

Nosso objetivo é calcular o intervalo de tempo necessário para parar a rotação da cápsula, então vamos isolar :

Falta encontrar uma expressão para a força exercida pelos jatos.

Quando expelimos de gás a cada segundo, com uma rapidez de , a força exercida é a seguinte:

Nesse caso, o segundo termo é nulo, já que a rapidez é constante, e ficamos apenas com o primeiro termo:

Substituindo isso na expressão de antes:

Agora é só determinar alguns valores numéricos:

E substituir