Exercícios de Momento Angular - Lista de Exercícios Resolvida
Questão 1
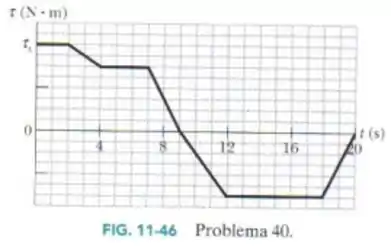
A Fig. 11-46 mostra o torque que age sobre um disco inicialmente estacionário que pode girar em torno do seu centro como um carrossel em função do tempo. Qual é o momento angular do disco em relação ao eixo de rotação nos intantes (a) e (b) ?
Questão 2
O momento angular de um volante com um momento de inércia de em relação ao eixo central diminui de para em . (a) Qual é o módulo do torque médio em relação ao eixo central que age sobre o volante durante esse período? (b) Supondo que uma aceleração angular constante, de que ângulo o volante gira? (c) Qual é o trabalho realizado sobre o volante? (d) Qual é a potência média do volante?
Ver solução completaQuestão 3
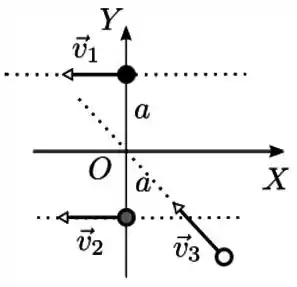
Três partículas de massas iguais a movem-se na ausência de forças externas com velocidades e . Num dado instante elas ocupam as posições indicadas na figura abaixo. O vetor momento angular total deste sistema de partículas em relação a origem do eixo de coordenadas da figura é
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 4
Considere uma partícula de massa presa ao teto em um suporte fixo por meio de um fio ideal de comprimento , formando um pêndulo. A partícula é solta a partir do repouso, com o fio esticado, a uma distância do teto; é o módulo da aceleração local da gravidade. Qual é o módulo do momento angular da partícula com relação ao ponto de sustentação do fio quando ela passa pelo ponto mais baixo da trajetória?
Questão 5
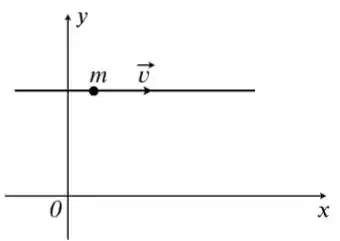
A figura mostra a trajetória reta de uma partícula de massa no plano com velocidade constante . É INCORRETO afirmar sobre o movimento que:
(a) o momento angular em relação a qualquer ponto do plano é constante.
(b) o momento angular em relação à origem é nulo.
(c) o momento angular em relação ao ponto de interseção da trajetória com o eixo é nulo.
(d) o torque total sobre a partícula é nulo.
(e) a força resultante sobre a partícula é nula.
Ver solução completaQuestão 6
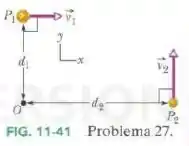
No instante da Fig. 11-41, duas partículas se movem em um plano . A partícula possui uma massa de e uma velocidade e está a uma distância do ponto . A partícula possui uma massa de e uma velocidade e está a uma distância do ponto . Quais são (a) o módulo e (b) a orientação do momento angular resultante das duas partículas em relação ao ponto ?
Questão 7
Um avião de está voando em uma linha reta a , acima do solo. Qual é o módulo do momento angular do avião em relação a um ponto no solo verticalmente abaixo do local onde ele se encontra?
Ver solução completaQuestão 8
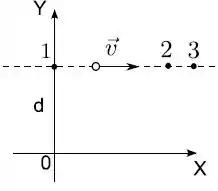
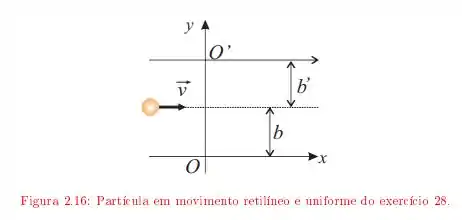
Uma partícula move-se com velocidade constante ao longo de uma reta paralela ao eixo que corta o em . Sejam , e os momentos angulares da partícula, relativos à origem , nos pontos , e , como indicados na figura. Os módulos dos momentos angulares são tais que
- ;
- ;
- ;
- ;
- e ;
Questão 9
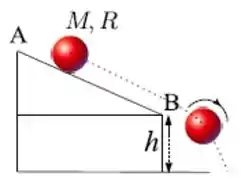
Uma esfera de massa , raio e momento de inércia , em relação ao eixo que passa pelo seu centro de massa, desce um plano inclinado (ver figura), rolando sem deslizar. A esfera parte do repouso e desce até o final do plano inclinado (ponto ), situado a uma altura em relação ao solo. Neste instante, ela tem velocidade angular , e entra em queda livre. Afirma-se que: Imediatamente antes de tocar o solo, a velocidade angular da esfera é . Imediatamente antes de tocar o solo, a velocidade angular da esfera continua com valor . O momento angular da esfera mantém-se perpendicular ao plano do movimento. Ao longo da queda livre, a energia cinética de rotação da esfera permanece constante. Qual(ais) da(s) afirmação(ões) acima está(ão) incorreta(s)?
- Somente a .
- Somente a .
- e .
- e .
- e .
Questão 10
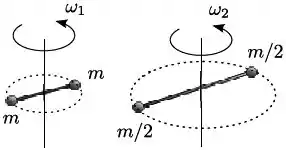
Um haltere é formado por duas partículas de massa , ligadas por uma barra rígida de massa desprezível e comprimento , e gira com velocidade angular em torno de um eixo fixo perpendicular a barra e passando pelo seu ponto médio. Um segundo haltere é formado por duas partículas de massa , ligadas por uma barra rígida de massa desprezível e comprimento , e gira com velocidade angular em torno de um eixo fixo perpendicular a barra e passando pelo seu ponto médio. Considerando que os halteres têm o mesmo momento angular, podemos afirmar que:
Questão 11
Uma chapa retangular é colocada para girar com velocidade angular constante de duas maneiras diferentes, 1 e 2, como indicado na figura. Nos dois casos os eixos de rotação passam pelos seus centros de massa. As relações entre os módulos dos momentos angulares e , e entre as energias cinéticas de rotação e nas duas situações são
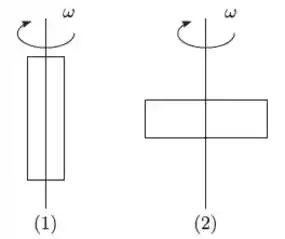
(a) e
(b) e
(c) e
(d) e
(e) e
Ver solução completaQuestão 12
Considere uma partícula de massa presa ao teto em um suporte fixo por meio de um fio ideal de comprimento , formando um pêndulo. A partícula é solta a partir do repouso, com o fio esticado, a uma distância do teto; é o módulo da aceleração local da gravidade. Qual é o módulo do momento angular da partícula com relação ao ponto de sustentação do fio quando ela passa pelo ponto mais baixo da trajetória?
Questão 13
Uma barra delgada homogênea e uniforme, de massa e comprimento , é articulada num pino , que passa por uma de suas extremidades, e pode girar sem atrito num plano vertical. Liberada a partir do repouso na posição horizontal, a barra sofre uma colisão elástica com um pêndulo ao passar pela posição vertical, como representa a massa de dimensões desprezíveis presa à extremidade da haste. O pêndulo também pode oscilar em torno do pino, sem atrito, no mesmo plano vertical que a barra. Sabe-se que o pêndulo encontrava-se em repouso antes da colisão com a barra, e que o momento de inércia da barra em relação ao eixo perpenducular ao plano vertical e que passa pelo pino é
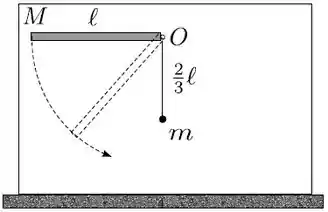
- Determine a velocidade angular da barra, , imediatamente antes da colisão com o pêndulo.
- Quais das seguintes grandezas: o momento linear e o momento angular em relação a são conservadas na colisão? Justifique a sua resposta.
- Determine a velocidade angular da barra, , imediatamente após a colisão.
- Determine o valor da razão para que a barra permaneça em repouso depois da colisão.
Questão 14
Qual é o ângulo entre o vetor momento linear de uma partícula e o seu vetor momento angular ? Justifique
Ver solução completaQuestão 15
Uma partícula de com uma velocidade de está passando pelo ponto . A partícula é puxada por uma força de no sentido negativo do eixo . Quais são , em relação à origem,
o momento angular da partícula
o torque que age sobre a partícula e
a taxa com a qual o momento angular está variando?
Ver solução completaQuestão 16
Uma partícula sofre a ação de dois torques em relação à origem: tem módulo de e aponta no sentido positivo do eixo , tem um módulo de e aponta no sentido negativo do eixo . Determine , onde é o momento angular da partícula em relação à origem, em termos dos vetores unitários.
Ver solução completaQuestão 17
Considere um sistema de cinco objetos puntiformes dispostos em um plano de acordo com a figura a seguir. Cada um dos quatro objetos periféricos possui massa igual a , enquanto que o quinto, localizado na origem do sistema de coordenadas indicado na figura, tem massa . Eles são unidos por hastes rígidas e de massas desprezíveis.
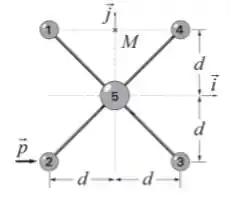
Calcule o momento de inércia do sistema em relação ao eixo passando pelos objetos e .
Calcule o momento de inércia do sistema em relação ao eixo perpendicular ao plano da figura e passando pela origem.
Calcule o momento de inércia do sistema em relação ao eixo perpendicular ao plano da figura e passando pelo ponto indicado na figura.
O sistema, inicialmente em repouso, recebe um impulso conforme ilustra a figura. Qual é a velocidade subsequente do centro de massa? Escreva sua resposta em função de , e .
Ainda considerando a situação descrita no item anterior, qual é a velocidade angular do sistema, em torno de seu centro de massa, imediatamente após o impulso? Escreva sua resposta em função de , e .
Após o impulso o sistema passa a rodar no sentido anti-horário do plano. Seja e . Obtenha o módulo e o sentido do torque aplicado no sistema por uma força resistiva, sabendo que a velocidade angular decresce linearmente de até em segundos.
Ver solução completaQuestão 18
Considere um projétil de massa movimentando-se no plano de um sistema de coordenadas nas situações descritas pelos itens abaixo. Adotamos nesta questão um sistema de unidades arbitrário, onde a constante gravitacional de Newton é igual a . Expresse seus resultados em função de onde for necessário.
O projétil desloca-se isoladamente em movimento retilíneo uniforme. Sua posição em função do tempo é dada por onde e são os versores dos eixos e , respectivamente. Qual é o módulo e o sentido do vetor momento angular do projétil com relação à origem desse sistema de coordenadas? Justifique.
Nos itens subsequentes, considere um planeta de massa , com , fixo na origem do sistema de coordenadas. Para os itens , e , o planeta é puntiforme e a condição inicial do projétil é e .
Determine o vetor momento angular e a energia total do projétil.
Qual é a forma geométrica que descreve a trajetória? Justifique. Dica: ache o raio de equilíbrio minimizando o potencial efetivo e tire suas conclusões.
Faça um esboço bem qualitativo da trajetória do projétil com relação à posição do planeta indicando, em dois pontos distintos da trajetória, as orientações dos versores das coordenadas polares.
O planeta agora é uma esfera de raio com densidade que varia radialmente de a de acordo com
Ou seja, é mais denso em seu centro do que em sua superfície. O projétil agora encontra-se em repouso na superfície do planeta. Partindo da equação da energia total do projétil obtenha a velocidade mínima, em termos de , para que o projétil escape para bem longe do planeta (velocidade de escape).
Ver solução completaQuestão 19
A figura mostra a trajetória reta de uma partícula de massa no plano com velocidade constante . É INCORRETO afirmar sobre o movimento que:
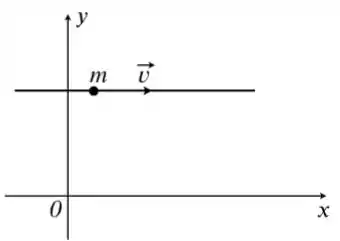
(a) o momento angular em relação a qualquer ponto do plano é constante.
(b) o momento angular em relação à origem é nulo.
(c) o momento angular em relação ao ponto de interseção da trajetória com o eixo é nulo.
(d) o torque total sobre a partícula é nulo.
(e) a força resultante sobre a partícula é nula.
Ver solução completaQuestão 20
Um cilindro oco (raio , ) rola para baixo em um plano inclinado (ângulo ) sem deslizar. Sobre a superfície do cilindro corre um menino (massa , que pode ser considerada como puntiforme), e ele consegue ficar sempre no ponto mais alto do cilindro. Considere .
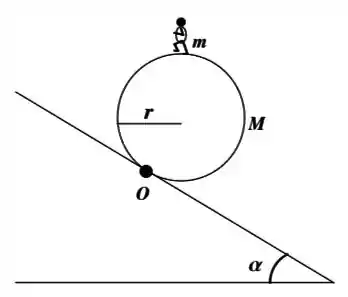
Calcule o momento de inércia do cilindro em relação ao eixo instantâneo .
Ache a expressão para momento angular do sistema em torno do ponto em termos das massas, ângulo, raio e velocidade do centro de massa.
Qual é o torque total de forcas externas sobre o sistema em relação do ponto ?
Calcule o módulo da aceleração do cento de massa do cilindro.
Ver solução completaQuestão 21
Imagine que um objeto de perfil circular (com raio , massa e momento de inércia ) seja colocado no ponto da canaleta ilustrada abaixo com velocidade inicial nula. O atrito entre esse objeto e a canaleta é suficiente para que ele role sem deslizar e a resistência do ar é desprezível.
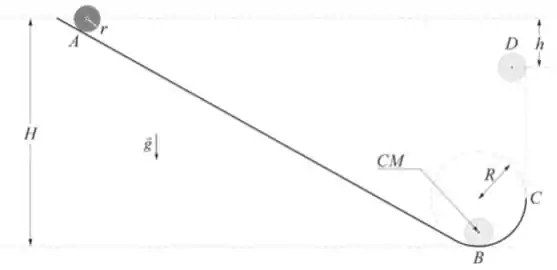
Esboce o diagrama das forças que agem sobre o objeto quando ele está no ponto da trajetória e escreva as equações do movimento, de translação e de rotação (não é necessário resolvê-las).
O ponto da trajetória indica o ponto mais alto que o objeto atinge após ser atirado verticalmente para cima, em . Explique em até duas linhas legíveis porque a velocidade angular do objeto, em torno do seu centro de massa, em e em são iguais.
Considere os seguintes perfis de densidade para o objeto (quanto mais escuro, mais denso), todos com a mesma massa. Liste-os, em ordem crescente de momento de inércia.

Para qual dos perfis acima o corpo sobe mais (ou seja, a distância é menor)?
Calcule a altura em função dos parâmetros , , , e .
Ver solução completaQuestão 22
Uma pá da hélice de um helicóptero pode ser considerada como sendo uma barra uniforme e longa. Se cada uma das três pás do rotor de um helicóptero possui de comprimento e de massa, determine:
(a) O momento de inércia de cada uma das três pás do rotor com relação ao eixo de rotação, e o momento de inércia do conjunto.
(b) O módulo, direção e sentido do torque (constante) que o motor deve exercer sobre o rotor para levá-lo (do repouso) a uma velocidade angular de rotações por segundo em segundos (deixe claro sua escolha de sistema de coordenadas).
(c) A energia cinética e o momento angular (módulo, direção e sentido) do conjunto em .
Dado: Para uma barra, o momento de inércia com relação ao eixo (perpendicular a barra) que passa pelo centro de massa vale .
Ver solução completaQuestão 23
Um disco de raio e massa e um cubo de lado e mesma massa, estão no topo de um plano com comprimento inclinado de com a horizontal. Existe atrito entre o plano inclinado e os dois objetos, os coeficientes de atrito cinético e atrito estático são respectivamente e . Na base do plano existe um trilho na vertical com o formato de um anel de raio como ilustra o desenho. A base do plano e o trilho têm superfícies com atrito desprezível. Na saída do trilho, está em repouso um segundo cubo idêntico ao primeiro com seu centro de massa na posição . Logo após o segundo cubo, a superfície horizontal apresenta um coeficiente de atrito cinético variável e no final desta superfície está uma mola com constante elástica . A superfície embaixo da mola tem atrito desprezível. A origem do sistema de coordenadas coincide com o centro do anel. A aceleração da gravidade é . Desenvolva as equações na forma literal para somente no final substituir as variáveis pelos valores fornecidos.
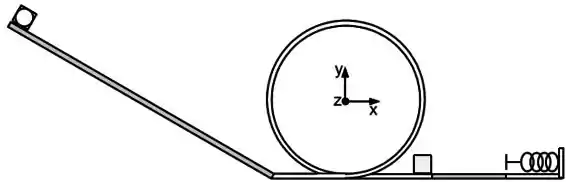
e) Imediatamente antes da colisão, calcule o momento angular , em relação à origem do sistema de coordenadas, do cubo que está em movimento. Suponha a velocidade do cubo imediatamente antes da colisão é de
Ver solução completaQuestão 24
Um mastro de uma bandeira pode ser modelado por um ahaste homogênea de massa e comprimento que tem presa em sua extremidade uma esfera sólida homogênea de massa e raio . O mastro está preso em sua outra extremidade a uma parede no ponto P, fazendo um ângulo com a horizontal, como ilustra a figura. Utilize g para a aceleração da gravidade.
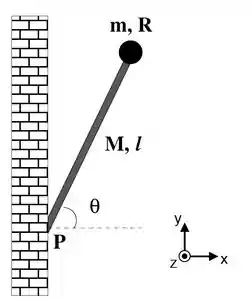
Calcule o momento de inércia rotacional do mastro em torno a um eixo perpendicular ao plano do papel (eixo ) que passe pelo ponto .
Calcule o vetor torque que a força da gravidade faz no mastro em relação ao ponto P.
Suponha que, devido a algum defeito na fixação da esfera, a mesma se solte da extremidade e caia verticalmente. Calcule o momento angular da esfera em relação aoponto P após ela ter caído durante um intervalo de tempo .
Ver solução completaQuestão 25
1) Um corpo de massa está preso à extremidade de um fio ideal que está enrolado numa peça composta por dois cilindros de massas e e raios e , que giram juntos sobre um eixo, como mostra a figura. O fio está enrolado em torno do cilindro e não desliza sobre ele.
O momento de inercia de um cilindro maciço é dado por:
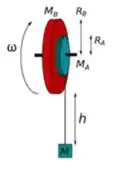
a) Faça um diagrama de corpo livre para o corpo de massa e para a peça composta por dois cilindros.
b) Suponha que não há perdas por atito. Use a 2ª Lei de Newton e seu análogo rotacional para calcular a aceleração do bloco de massa em função das variáveis dadas no problema.
Ver solução completaQuestão 26
Um carrossel de raio com momento de inércia gira com velocidade angular . Uma pessoa de massa está parada próximo à borda do carrossel. A pessoa sobre no carrossel; sua velocidade antes de pisar no carrossel era desprezível. Responda justificando:
Qual será a velocidade angular do carrossel logo depois que a pessoa sobre?
Ver solução completaQuestão 27
Qual é o módulo e a direção do momento angular de um disco homogêneo de massa 2,0 kg e diâmetro 4,0 cm girando com velocidade angular ω = 100 rad/s em torno de um eixo perpendicular ao seu plano e que passa pelo seu centro?
Ver solução completaQuestão 29
Um carrossel tem raio de e momento de inércia em relação ao seu eixo de . O carrossel está inicialmente em repouso quando uma menina de começa a caminhar sobre o carrossel com velocidade de em relação ao solo, tangente ao círculo de raio e concêntrico com o carrossel. Considere a menina como uma partícula e despreze o atrito no eixo do carrossel.
- A partir do instante em que a meina inicia a caminhada, qual o torque resultante externo, sobre o sistema {carrossel menina}, em relação ao eixo do carrossel?
- Calcule a velocidade angular do carrossel.
- O que acontecerá com o carrossel se inicialmente, ao invés de caminhar na direção tangencial, a menina caminhasse em direção ao centro do carrossel (direção radial)?
Questão 30
Uma partícula de massa é lançada obliquamente de forma que sua velocidade inicial tem módulo e forma um ângulo com a horizontal. O momento angular da partícula no ponto mais alto de sua trajetória, calculado com relação ao ponto de lançamento tem módulo igual a:
(a)
(b)
(c)
(d)
(e)
(f)
Ver solução completaQuestão 31
Qual das seguintes afirmações é correta?
(A) O momento angular de um sistema de partículas é a soma do momento angular em relação ao CM com o momento angular do CM.
(B) O momento angular de um sistema de partículas é o momento angular em relação ao CM.
(C) O momento angular de um sistema de partículas é o momento angular do CM.
(D) O momento angular de um sistema de partículas é a soma do momento angular em relação ao CM com o momento linear do CM.
(E) O momento angular de um sistema de partículas é a soma do momento linear em relação ao CM com o momento angular do CM.
Ver solução completaQuestão 32
Considere uma estação espacial em formato de anel de raio igual a e massa igual a . Para que um tripulante da estação espacial sinta, sobre a superfície do anel, uma aceleração de queda livre efetiva igual a (use ), determine a velocidade angular (em ) e o momento angular (em ) da estação espacial girando em torno de seu eixo de simetria. O momento de inércia de um anel, com relação ao seu eixo de simetria, é igual a sua massa vezes o raio ao quadrado.
A. e
B. e
C. e
D. e
E. e
Ver solução completaQuestão 33
Quais afirmações sobre o momento angular de uma partícula são verdadeiras:
- A unidade de no SI é
- é paralelo ao vetor velocidade da partícula
- é perpendicular ao vetor momento linear e ao vetor da partícula
- independe da escolha da origem
- é nulo quando o vetor posição está perpendicular ao vetor momento linear
Escolha uma opção:
- I,III, IV e V
- I e III
- I, III e IV
- I, II, III
- I, III, V
Questão 34
Um projétil de massa é lançado de um ponto O de um plano horizontal com velocidade de módulo e ângulo de lançamento, onde . O projétil atinge uma altura máxima H e um alcance A. Se é o módulo do momento angular do projétil ao atingir a altura máxima H e , o módulo do momento angular quando ele atinge o alcance A, ambos calculados em relação a O, então
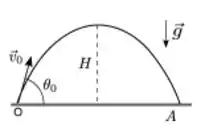
- Nenhuma das alternativas
Questão 35
Parte I: Duas hastes iguais muito finas de comprimento e massa estão coladas em forma de um conforme ilustra a figura. O momento de inércia rotacional do conjunto em torno do eixo tracejado é:
(a)
(b)
(c)
(d)
(e) nenhuma das respostas acima.
Parte II: Uma corpo de massa está conectado a uma corda que está firmemente enrolada em um cilindro de massa e raio . No instante abaixo o cilindro gira com velocidade angular e o corpo desce com velocidade de módulo igual a . A corda não desliza sobre o cilindro. Despreze a massa da corda e atritos. O módulo do momento angular do conjunto em relação ao centro do cilindro é:
(a)
(b)
(c)
(d)
(e) nenhuma das respostas acima.
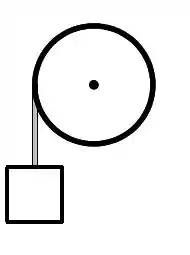
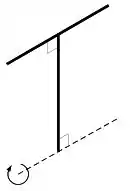
Parte III: Seja uma barra de comprimento e peso sobre a qual agem as forças ilustradas ao lado. O módulo do torque resultante em torno da extremidade superior é:
(a)
(b)
(c)
(d)
(e) nenhuma das respostas acima.
Questão 36
Um ginasta executa um salto mortal. Para isso, enquanto está no ar, dobra o corpo. Podemos dizer que durante sua subida no salto, após perder o contato com o solo, seu momento de inércia em relação ao eixo passando pelo seu centro de massa (perpendicular ao plano do desenho), seu momento angular em relação ao seu centro de massa e sua energia mecânica total, respectivamente,
a) Diminui, se mantém, se mantém.
b) Diminui, se mantém,aumenta.
c) Diminui, diminui, diminui.
d) Aumenta, aumenta, aumenta.
e) Aumenta, diminui, se mantém.
Questão 37
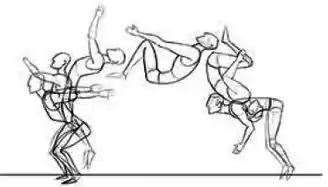
Uma partícula de massa se move com velocidade numa trajetória circular de raio sobre uma mesa sem atrito. A partícula está presa em uma corda que passa por um buraco no centro da mesa como ilustra a figura abaixo. A corda é puxada lentamente para baixo até que a partícula atinja uma distância do buraco e começa a se mover numa nova trajetória circular de raio .
a) Calcule a velocidade final da partícula em função de , e .
b) Calcule a tensão quando a partícula se move numa trajetória circular de raio em termos de e do momento angular .
c) Calcule o trabalho feito pela força de tensão na partícula por integrar . Expresse a resposta em termos de e .
Questão 38
Um capacitor de é carregado a uma tensão de e então é ligado a um indutor de . A frequência angular de oscilação das energias armazenadas no campo elétrico do capacitor e no campo magnético do indutor é:
Questão 39
Um homem com os braços junto ao corpo está em cima de uma mesa que gira praticamente sem atrito. Quando o homem estende os braços pra fora:
- A energia cinética do sistema aumenta
- O momento angular do sistema continua o mesmo
- A velocidade angular da mesa aumenta
- A velocidade angular da mesa continua a mesma
- O momento de inércia do homem diminui
Questão 40
Um disco sólido de massa , raio e momento de inércia rola sem deslizar ao longo de uma superfície com velocidade constante e velocidade angular . Qual é o momento angular do disco em relação ao seu próprio eixo enquanto ele rola?
Questão 41
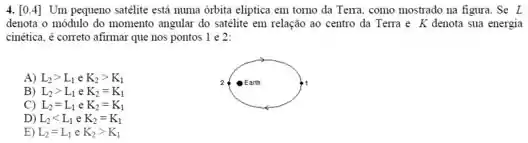
Sob a ação da força de atração gravitacional, um satélite artificial descreve uma órbita elíptica em torno da terra. Qual das quantidades abaixo permanece constante ao longo da trajetória do satélite?
- O vetor momento angular do satélite em relação ao centro da terra.
- O módulo do vetor velocidade do satélite.
- A energia cinética do sistema.
- O vetor momento linear do satélite.
- O vetor aceleração tangencial do satélite.
Questão 42
No caso que uma roda (como mostra a figura ao lado) tem uma velocidade angular grande experimenta um movimento de precessão. ( é o torque, é a velocidade angular de precessão e é o momento angular).
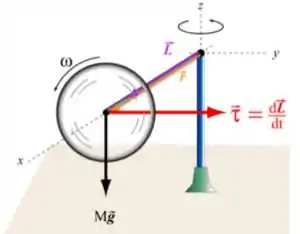
- A magnitude de varia devido ao torque;
- ;
- A velocidade angular de precessão é paralela ao torque.
- I e II
- I e III
- Apenas I
- Apenas II
- Apenas III
Questão 43
O vetor posição de uma partícula de massa que move-se no plano é dado por , onde é dado em metros e em segundos. O momento angular em relação à origem é:
Questão 44
A figura abaixo mostra uma chapa retangular, de comprimento e largura , que pode girar sem atrito em torno de um eixo perpendicular à figura que passa por um de seus vértices (ponto ). Duas forças e , cujos módulos são iguais a e independem do tempo , são aplicadas ao sistema paralelamente às arestas da chapa, conforme mostra a figura. Em a chapa se encontra em repouso.
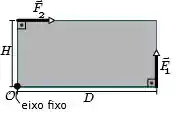
Com respeito ao módulo do momento angular da chapa em relação a O, pode-se afirmar que:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 45
Duas partículas de mesma massa se movem sobre uma reta com velocidades constantes, de mesmo módulo e sentidos contrários. Sobre esse sistema são feitas as seguintes afirmações:
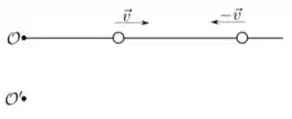
I. O momento angular de ambas as partículas com relação ao ponto é nulo
II. O momento angular de ambas as partículas com relação ao ponto é nulo
III. O momento angular total do sistema com relação aos pontos e é nulo
As afirmativas corretas são:
a) Todas as afirmativas.
b) Apenas I
c) Apenas II
d) Apenas III
e) Apenas I e II
f) Apenas I e III
g) Apenas II e III
h) Nenhuma das afirmativas.
Ver solução completaQuestão 46
Q - Uma partícula de massa , que pode mover-se em um plano , inicialmente em repouso na posição , é sujeita à aceleração . Ao final de segundos, contados a partir do início do movimento, o módulo do momento angular da partícula em relação à origem do sistema de coordenadas, em , é:
Ver solução completaQuestão 47
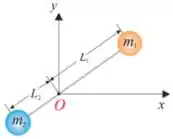
Q - Um sistema é formado por duas partículas de massas e presas às extremidades de uma barra rígida de massa desprezível. O sistema gira na ausência de atrito em um plano horizontal , em torno do ponto fixo , conforme mostra a figura. As distâncias das massas e em relação à são e , respectivamente. Se o módulo da velocidade da partícula de massa é , o módulo do momento angular do sistema em relação ao ponto , em , é:
Questão 48
(Cap 10 – Ex 37) Uma partícula de se move diretamente para o leste com uma rapidez constante de , ao longo de uma linha oeste-leste. (a) Qual é sua quantidade de movimento angular (incluindo a orientação) em relação a um ponto que está a ao norte da linha? (b) Qual é sua quantidade de movimento angular (incluindo a orientação) em relação a um ponto que está a ao sul da linha? (a) Qual é sua quantidade de movimento angular (incluindo a orientação) em relação a um ponto que está a diretamente a leste da linha?
Ver solução completaQuestão 49
Das partículas e , com a mesma massa, descrevem circunferências concêntricas de raios e , respectivamente, sendo . Os sentidos de giro das partículas são opostos, com velocidades de mesmo módulo. Quais das afirmativas que seguem são corretas?
(I) Os momentos angulares das duas partículas em relação ao centro das trajetórias têm mesmos direção e sentido.
(II) O módulo do momento angular do sistema formado pelas duas partículas em relação ao centro das trajetórias é nulo.
(III) O momento linear do sistema formado pelas duas partículas é sempre nulo.
a) nenhuma está correta
b) apenas (I)
c) apenas (III)
d) apenas (I) e (II)
e) apenas (II) e (III)
f) apenas (I) e (III)
g) todas estão corretas
h) apenas (II)
Ver solução completaQuestão 50
Uma pedra com massa tem uma velocidade horizontal com magnitude de quando se encontra no ponto , como mostrado na figura. Neste momento, quais são a magnitude e a direção de seu momento angular em relação ao ponto ?
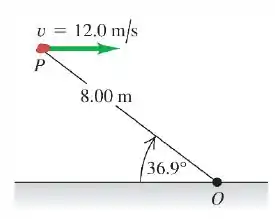
(A) , para dentro da página.
(B) , para fora da página.
(C) , para dentro da página.
(D) , para fora da página.
(E) , para fora da página.
Ver solução completaQuestão 51
Duas partículas, com massas e , estão ligadas por uma haste de massa desprezível e comprimento , conforme indicado na figura abaixo.
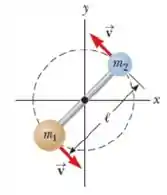
Em um determinado instante de tempo , o sistema começa a girar no plano em torno de um eixo de rotação que passa pelo centro da haste. Sabendo que o momento de inércia do sistema em relação ao eixo de rotação é , quando o módulo da velocidade radial de cada partícula é , o comprimento da haste é dado por:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 52
Uma polia com momento de inércia em relação ao eixo e raio é submetida a uma força aplicada tangencialmente à sua borda de módulo com em Newtons e em segundos. Admitindo que a polia está inicialmente em repouso, determine a velocidade angular da polia no instante .
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 53
Um spinner possui momento de inércia em relação ao eixo de simetria que passa pelo seu centro de massa. Inicialmente ele é posto para girar com velocidade angular de módulo em torno de um eixo vertical que passa pelo seu centro de massa. Em um determinado instante a pessoa que o segura muda a posição de sua mão de forma a ter um plano de rotação vertical. Com este movimento a velocidade angular do spinner é reduzida para de seu valor inicial. Qual é o módulo da variação do momento angular do spinner devido a sua mudança do plano de rotação?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Ver solução completaQuestão 54
Uma partícula de massa move-se no plano . Em um determinado instante a partícula está a uma distância da origem e sua velocidade tem módulo de e faz um ângulo de com a direção radial (), como mostra a figura. Neste instante, o vetor momento angular da partícula em relação à origem é:
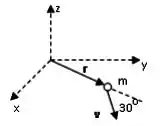
(A) Zero
(B)
(C)
(D)
(E)
Ver solução completaQuestão 55
Uma partícula se move com velocidade constante . Sobre o momento angular dessa partícula em relação à origem de um determinado sistema de eixos pode-se afirmar que:
(a) O momento angular de uma partícula com velocidade constante sempre é nulo.
(b) Não pode ser nulo em nenhum instante.
(c) Será nulo apenas no instante em que a partícula cruzar um dos eixos cartesianos.
(d) É nulo em todos os instantes se a trajetória da partícula passa pela origem em algum momento.
Ver solução completaQuestão 56
Três partículas de massa estão presas a hastes de tamanho e massas desprezíveis, como uma hélice. O sistema pode girar em torno de um eixo fixo que passa pelo seu centro, , e inicialmente possui velocidade angular . Um chiclete de massa incide com velocidade conforme a figura, e realiza uma colisão perfeitamente inelástica com uma das massas .
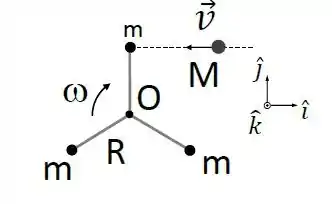
Julgue as seguintes assertivas
I. O momento de inércia do sistema composto pelas 3 massas é em relação ao eixo de rotação.
II. O momento angular inicial do sistema composto pelas 3 massas m aponta na direçãoem relação ao eixo de rotação.
III. O momento angular da massa antes da colisão tem módulo em relação ao eixo de rotação.
Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).
(A) I
(B) II
(C) III
(D) I e II
(E) I e III
(F) II e III
(G) Todas
(H) Nenhuma
Ver solução completaQuestão 57
Um objeto tem momento de inércia com respeito ao seu eixo de simetria de e está sujeito a um torque paralelo ao eixo de simetria e com respeito a um ponto sobre este eixo. A magnitude do torque é mostrada no gráfico. Se o objeto está inicialmente em repouso, a magnitude da velocidade angular do objeto em é:
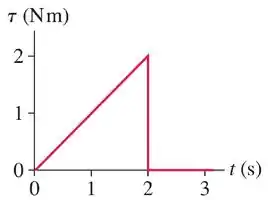
A.
B.
C. impossível determinar, pois o torque depende da distância do ponto de aplicação da força ao eixo de rotação e da magnitude da força.
D.
E.
Ver solução completaQuestão 58
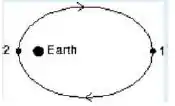
Um pequeno satélite está em uma órbita elíptica em torno da Terra, como mostrado. Comparando o momento angular L do satélite e a sua energia cinética nos pontos e , podemos afirmar:
Questão 59
Uma haste rígida de massa e comprimento pode girar sem atrito em torno do seu centro fixo , como na figura. Duas partículas de massas e são presas às suas extremidades. Este sistema gira em torno do ponto , num plano vertical, com uma velocidade angular instantânea . O módulo do momento angular do sistema é:
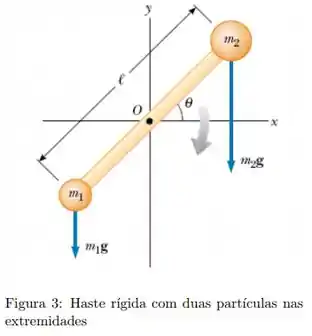
Dados: Momento de inércia de uma barra uniforme (massa , comprimento ) em relação ao eixo que passa pelo centro de massa e é perpendicular ao comprimento da barra: .
A.
B.
C.
D.
E.
Ver solução completaQuestão 60
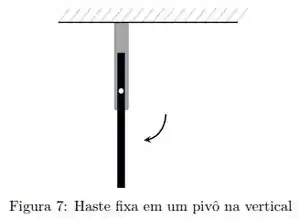
Uma haste longa e fina de massa e comprimento é livre para girar sobre um ponto localizado a de seu comprimento. A haste é posicionada na posição horizontal, como mostrado na figura , por um fio preso na extremidade:
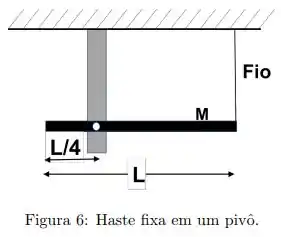
Em um dado momento o fio é cortado e a haste fica livre para girar em torno do eixo.
Dados: Momento de inércia em relação ao eixo de rotação perpendicular a haste e passando pelo pivô é
(d) Determine o momento angular da haste relativo ao pivô no momento em que a haste alcança a posição vertical.
Questão 61
Um disco de vinil horizontal de massa e raio gira livremente em torno de um eixo vertical que passa pelo centro com uma velocidade angular de . O momento de inércia do disco em relação ao eixo de rotação é . Um pedaço de massa de vidraceiro úmida de massa cai verticalmente e gruda na borda do disco. Qual é a velocidade angular do disco imediatamente após a massa cair?
Ver solução completaQuestão 62
Uma partícula de com uma velocidade de está passando pelo ponto . A partícula é puxada por uma força de no sentido negativo do eixo . Quais são, em relação à origem,
o momento angular da partícula
o torque que age sobre a partícula e
a taxa com a qual o momento angular está variando?
Ver solução completaQuestão 63
Uma porta de e de largura, suspensa por dobradiças bem azeitadas, está aberta de , ou seja, com seu plano perpendicular ao plano do batente. Ela leva um empurrão na beirada aberta, com um impacto equivalente ao de uma massa de , com velocidade . Quanto tempo ela leva para fechar-se?
Ver solução completaQuestão 64
Um pêndulo é constituído por uma partícula de massa m e um fio ideal de comprimento d preso ao teto em um ponto de fixação O. A partícula é solta a partir do repouso com o fio tensionado e fazendo um ângulo θ com a vertical (posição A). Quando o fio passa pela posição vertical a partícula tem uma velocidade de módulo v. Tomando todos os momentos angulares e torques relativos ao ponto de fixação O, denotando por e os momentos angulares da partícula nas posições A e B, e por e os torques sobre a partícula nas posições A e B, respectivamente, podemos afirmar que:
- e
- e
- e
- e
- e
Questão 65
Uma esfera rola sem deslizar por uma superfície horizontal de maneira que a velocidade de seu centro de massa é constante . A figura mostra duas vistas da situação: à esquerda uma vista do alto da mesa e à direita uma vista por trás da esfera.
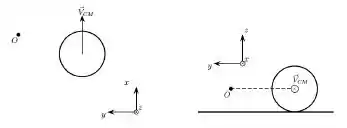
Em relação ao ponto O, indicado na figura, que está a mesma altura da posição do centro de massa da esfera, no sistema de eixos também indicado na figura, é correto afirmar que o momento angular da esfera tem componentes não nulas:
(a) .
(b) Apenas .
(c) Apenas .
(d) Apenas .
(e)
(f)
(g) Todas as 3 componentes.
Ver solução completaQuestão 66
Duas barras finas de mesmos comprimento e massa são dobradas com aberturas de ângulos . Elas são colocadas para girar em torno dos eixos de simetria que passam pelos seus vértices, com mesma velocidade angular constante, como mostra a figura. Sobre sua energia cinética e o módulo do momento angular referido ao eixo de rotação é correto afirmar que:
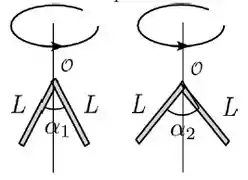
(a) ;
(b) ;
(c) ;
(d) ;
(e) ;
(f) ;
(g) ;
Ver solução completaQuestão 67
Considere um sistema formado por uma partícula e por uma mola ideal, conforme a figura. A partícula pode mover-se sobre uma mesa horizontal lisa sob a ação da força da mola, cuja outra extremidade está presa à mesa. É correto afirmar que:
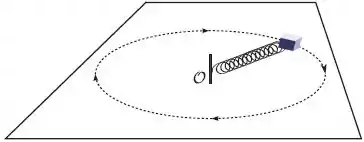
- O momento angular não se conserva consequência da ação da força elástica.
- O trabalho da força elástica é nulo, pois trata-se de uma força conservativa.
- O sentido da rotação em torno do centro de forças pode mudar pela ação da força elástica.
- A energia mecânica sempre aumenta porque sempre há energia potencial armazenada na mola.
- O momento angular se conserva porque a reta de ação da força elástica sobre a partícula passa pela origem .
Questão 69
A figura mostra um sistema mecânico simples. Uma haste delgada de massa e comprimento está presa em uma extremidade por um pino e livre para girar sem atrito. Na outra extremidade se encontra presa uma esfera de massa e raio desprezível. Considere e a distância vertical
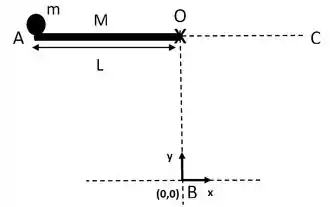
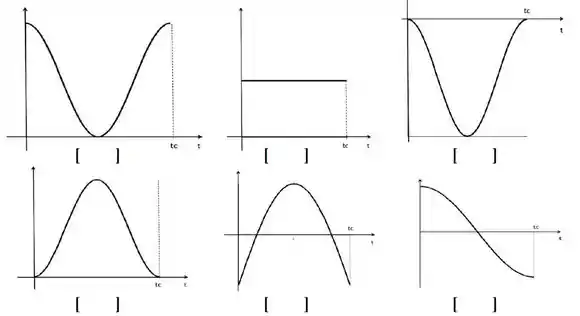
Considere agora o movimento do sistema abandonado do repouso no ponto A. Indique com o número apropriado o gráfico que representa cada uma das grandezas físicas do movimento em função do tempo até que o sistema finalmente alcance novamente o repouso no ponto C.
[1] O Momento Angular Total do Sistema.
[2] O Torque que Atua no Sistema
[3] A Energia Potencial Gravitacional.
[4] A Energia Mecânica Total
[5] A variação da Energia Potencial Gravitacional.
Questão 70
11. Um haltere consiste de duas massas ligadas por uma haste rígida de massa desprezível e
comprimento . Um estudante segura o haltere e, fazendo-o girar em torno de seu centro de massa, confere a ele um momento angular . O estudante então segura um segundo haltere, com massas e comprimento , fazendo-as girarem com a mesma velocidade
angular. Qual é o momento angular do segundo haltere em relação ao primeiro?
![]()
;
;
;
;
;
Ver solução completaQuestão 71
Um cilindro rígido homogêneo de raio rola sem deslizar para a direita sobre o trecho AB de uma mesa horizontal com velocidade do centro de massa constante de módulo , como mostrado na figura, sendo o coeficiente de atrito estático entre o cilindro e o trecho AB da mesa.
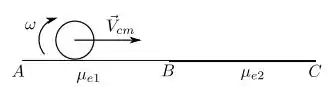
No avanço, entra no trecho BC, no qual o coeficiente de atrito estático com o cilindro é = .
Selecione a resposta correta:
- O momento angular do cilindro em torno de seu eixo de simetria permanece constante.
- O cilindro começa a deslizar.
- A velocidade de translação é duas vezes menor.
- O torque da força de atrito estática em relação ao eixo de simetria do cilindro é duas vezes maior.
- A energia cinética total diminui.
- O cilindro continua rolando sem deslizar, mas a condição de rolamento puro passa a ser .
Questão 72
[ENUNCIADO COMUM ÀS QUESTÕES 5 E 6]
Uma barra delgada de massa e comprimento é mantida na vertical com uma das extremidades apoiada no solo e depois é liberada. A extremidade superior atinge o solo sem que a extremidade de apoio deslize. Considere e que o momento de inércia de uma barra de massa e comprimento em torno de um eixo que passa pelo seu centro de massa é .
[QUESTÃO 5]
Qual é o momento angular (em ) da barra quando sua velocidade angular é ?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 73
Duas partículas se movem em sentidos opostos sobre uma reta. A partícula de massa desloca-se para a direita, com velocidade, enquanto a partícula de massa se desloca para a esquerda, com velocidade. Qual o momento angular total do sistema em relação
(a) ao ponto A,
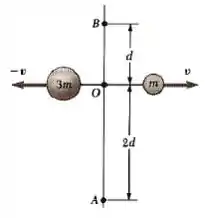 (b) ao ponto O e
(b) ao ponto O e
(c) ao ponto B?
Ver solução completaQuestão 74
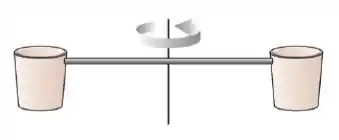
Um sistema formado por dois baldes e uma barra estão fixados a um eixo como indicado na figura. O sistema, que gira em torno do eixo com uma certa velocidade angular, descreve um círculo no plano perpendicular ao eixo. De repente começa a chover. Despreze qualquer tipo de atrito e força de resistência. Pode-se afirmar que:

Questão 75
O vetor fornece a posição de uma partícula de massa no instante em relação à origem de um sistema de coordenadas . Determine o módulo do momento angular da partícula em relação à origem no instante .
Ver solução completaQuestão 76
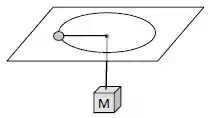
Um corpo de massa desliza sobre uma superfície horizontal, preso a um fio que passa por um furo. A extremidade do fio está presa a uma massa . O corpo de massa gira sem atrito, fazendo uma trajetória raio , com velocidade angular suficiente para manter a massa suspensa. Se a massa suspensa cair para a metade do seu valor inicial, qual a razão entre o raio final e o raio inicial ?
Questão 77
Um objeto de 1,4 Kg, localizado em x = 2,0 m, y = 3,1 m, se move a 4,62 m/s em uma direção que faz 45 graus com a horizontal. Com relação à origem, o módulo do momento angular do objeto vale:
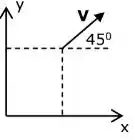
a) 3,6
b) 5,0
c) 6,0
d) 7,0
e) 23
Ver solução completaQuestão 78
Um aro de massa e raio está em repouso no topo de um plano inclinado, como mostrado. O aro rola plano abaixo sem deslizar. Quando ele atinge a base do plano seu momento angular em torno de seu centro de massa é:
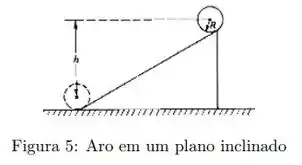
Dados: Momento de inércia de um anel uniforme (massa , raio ) em relação ao eixo que passa pelo centro de massa e é perpendicular ao plano do anel: .
A.
B.
C.
D.
E.
Ver solução completaQuestão 79
- Uma bola de argila de massa desloca-se com velocidade quando colide com outra bola de argila de massa que se desloca com velocidade . Sendo a colisão perfeitamente inelástica, a velocidade final das bolas será:
Ver solução completaQuestão 80
Uma partícula de massa amarrada a um barbante de massa desprezível gira sobre uma mesa sem atrito, percorrendo uma circunferência de raio em torno do ponto . A pessoa que segura o barbante diminui lentamente o raio da circunferência até que .
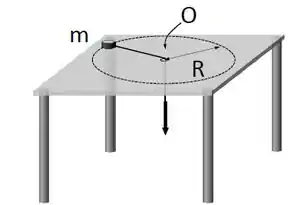
Considere as seguintes afirmativas relativas ao movimento da partícula:
I. O momento angular da partícula em relação a se conserva.
II. A velocidade angular da partícula em torno de aumenta.
III. O momento de inércia da partícula em relação a diminui.
É correto apenas o que se afirma em:
(A) I
(B) II
(C) III
(D) I e II
(E) I e III
(F) II e III
(G) Todas
(H) Nenhuma
Ver solução completaQuestão 81
Um aro elíptico homogêneo de massa é posto para girar com velocidade ao redor do seu eixo maior, em relação ao qual tem momento de inércia . Em seguida, é colocado para girar com mesma velocidade angular ao redor de seu eixo menor, em relação ao qual tem momento de inércia . Veja as figuras. Sobre os módulos dos momentos angulares e dos aros nas respectivas situações e , podemos afirmar que:
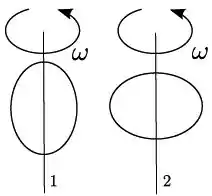
- , pois o momento de inércia ;
- , pois trata-se do mesmo sistema girando com a mesma velocidade angular;
- , pois o momento de inércia ;
- , pois o momento de inércia ;
- , pois o momento de inércia ;
Questão 82
A figura ,que se refere às Questões 1, 2 e 3, representa um aro que rola sem deslizar sobre uma superfície horizontal.
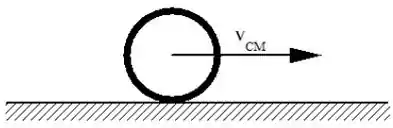
É correto afirmar que o vetor momento angular do aro em relação ao seu centro de massa
(A) aponta para dentro do papel.
(B) aponta para fora do papel.
(C) aponta para a esquerda.
(D) aponta para a direita.
(E) varia de ponto para ponto do aro.
Ver solução completaQuestão 83
Considere as afirmativas abaixo:
(I) Em uma colisão inelástica, o momento linear do sistema nunca é conservado.
(II) A velocidade do centro de massa de um sistema de partículas é sempre constante.
(III) Forças internas nunca alteram o momento linear total de um sistema de partículas.
(IV) O momento linear e o momento angular de um sistema de partículas sempre se conservam sob a ação de um par de forças externas de mesmo módulo, direção e sentidos opostos.
São verdadeiras apenas as afirmativas:
(a) I
(b) III
(c) II e IV
(d) II e III
(e) III e IV
Ver solução completaQuestão 84
Três partículas de massas iguais a movem-se na ausência de forças externas com velocidades e . Num dado instante elas ocupam as posições indicadas na figura abaixo. O vetor momento angular total deste sistema de partículas em relação a origem do eixo de coordenadas da figura é
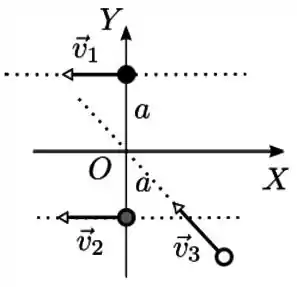
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 85
Uma partícula descreve uma trajetória circular com módulo da velocidade constante.
Como se altera o seu momento angular se o módulo do momento linear for duplicado?
Se o raio do círculo for triplicado, porém o módulo da velocidade se mantiver inalterado, como se altera o momento angular da partícula?
Ver solução completaQuestão 86
8) Em uma primeira situação, uma barra delgada e homogênea que pode girar em torno de um eixo ortogonal a ela e que passa por uma de suas extremidades tem aplicada na outra extremidade uma forca que é, também, ortogonal a ela. Verifica-se que após um intervalo de tempo de ação da força a barra adquire uma velocidade angular de módulo ao partir do repouso. Na segunda situação, uma outra barra, agora não homogênea em que a massa se encontra concentrada mais próxima ao eixo de rotação, a ação da mesma força e nas mesmas condições acaba produzindo uma velocidade angular final de módulo ao cabo do mesmo intervalo de tempo. Nessas condições, se e forem, respectivamente, os módulos dos momentos angulares finais das duas barras, devemos observar as seguintes relações
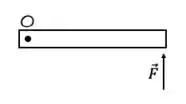
- e
- e
- e
- e
- e
Questão 87
Uma partícula de massa se move no plano com velocidade de módulo ao longo da direção dada pelo vetor . Calcule o momento angular da partícula em relação à origem do sistema de coordenadas em . Assinale a resposta correta.
(a)
(b)
(c)
(d)
(e) 0
Ver solução completaQuestão 88
Os dois sistemas mostrados na figura estão livres para girar em torno de eixos fixos que passam pelo centro dos discos. Eles diferem apenas pelas duas massas móveis posicionadas a diferentes distâncias do eixo de rotação. Se os blocos, que são iguais, são liberados simultaneamente a partir do repouso, qual das afirmações abaixo é correta?

(A) O bloco da direita chegará primeiro ao chão porque o momento de inércia em relação ao eixo de rotação é maior.
(B) O bloco da direita chegará primeiro ao chão porque o momento de inércia em relação ao eixo de rotação é menor.
(C) O bloco da esquerda chegará primeiro ao chão porque o momento de inércia em relação ao eixo de rotação é maior.
(D) O bloco da esquerda chegará primeiro ao chão porque o momento de inércia em relação ao eixo de rotação é menor.
(E) Os blocos chegarão ao chão ao mesmo tempo.
Ver solução completaQuestão 89
Uma partícula de massa move-se com velocidade constante em uma trajetória retilínea, como mostra figura .
Qual é o momento angular dessa partícula em relação ao ponto ? E em relação ao ponto ?
Questão 90
Dois patinadores, cada um de massa , deslizando sobre uma pista de gelo, com atrito desprezível, aproximam-se com velocidades iguais e opostas de módulo , segundo retas paralelas, as quais estão separadas por uma distância .
Calcule o vetor momento angular do sistema e mostre que é o mesmo em relação a qualquer ponto e se conserva.
Ver solução completaQuestão 91
Dois patinadores, cada um de massa , deslizando sobre uma pista de gelo, com atrito desprezível, aproximam-se com velocidades iguais e opostas de módulo , segundo retas paralelas, as quais estão separadas por uma distância .
Quando os dois patinadores chegam a uma distância um do outro, estendem os braços e dão-se as mãos, passando a girar em torno do centro de massa do sistema. Calcule a velocidade angular.
Ver solução completaQuestão 92
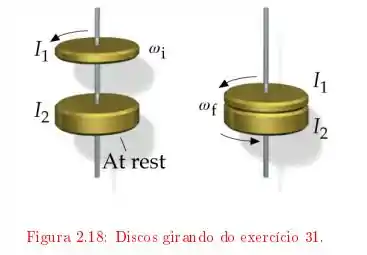
Um disco com momento de inércia , está girando, com velocidade angular em torno de um eixo sem atrito. Num certo instante, este disco cai sobre outro disco, de momento de inércia , que está inicialmente em repouso, no mesmo eixo. Em virtude do atrito entre as superfícies, os dois discos terminam por atingir uma velocidade angular comum a ambos . Determine . A energia cinética do sistema se conserva?
Questão 93
40. Uma bola de futebol, de massa e com diâmetro , rola sem deslizar sobre um plano inclinado. Ela parte do repouso e, depois de e tendo completado exatamente rotações, escapa pela borda do plano inclinado. Dado: .
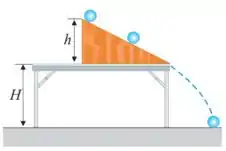
(b) Calcule a energia de rotação da bola ao colidir com o solo
Ver solução completaQuestão 94
Uma patinadora no gelo executa sua apresentação e começa a girar de braços abertos, com uma certa velocidade angular. Ao fechar os braços, qual das quantidades, relacionadas à patinadora, �� conservada?
(a) Momento angular em relação a seu eixo de rotação.
(b) Momento de inércia em relação a seu eixo de rotação.
(c) Velocidade angular de rotação.
(d) Energia cinética de rotação.
Ver solução completaQuestão 95
Dois alteres e mostrados na figura giram em torno de seus respectivos centros de massa em torno de um eixo fixo e perpendicular ao seu comprimento. O haltere gira com velocidade angular constante e o haltere com velocidade angular constante . No haltere as massas de suas extremidades são iguais a e no haltere . Os módulos de seus momentos angulares e em relação aos respectivos centros de massa e as suas energias cinéticas e cinéticas são relacionados respectivamente como
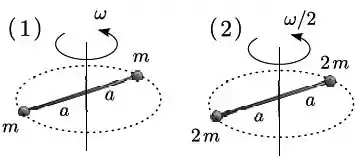
- e
- e
- e
- e
- e
Questão 96
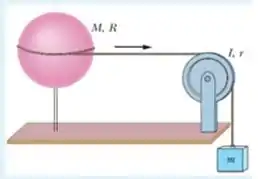
Uma esfera oca uniforme de massa e raio pode girar em torno de um eixo vertical sem atrito conforme a figura abaixo. Uma corda de massa desprezível esta enrolada no equador da esfera, passa por uma polia (um disco homogêneo) de massa e raio , e está presa a um pequeno objeto de massa . Não há atrito no eixo da polia, e a corda não escorrega na casca nem na polia. O sistema é liberado do repouso e o bloco cai de uma altura . No instante final da queda do bloco por essa distância , determine:
- O módulo da velocidade do bloco
- O módulo do momento angular da esfera com relação ao seu eixo de rotação
- O módulo do momento angular da polia com relação ao seu eixo de rotação.
Questão 97
A figura mostra um sistema mecânico simples. Uma haste delgada de massa e comprimento está presa em uma extremidade por um pino e livre para girar sem atrito. Na outra extremidade se encontra presa uma esfera de massa e raio desprezível. Considere e a distância vertical
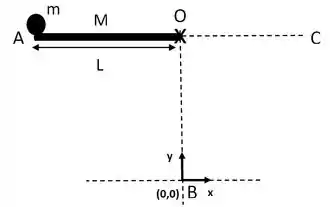
Dados:
-
-
-
-
Determine
- Uma expressão literal para o momento de inércia do sistema em relação ao ponto fixo , contendo somente as variáveis indicadas no enunciado.
- Um valor numérico para este momento de inércia.
- O momento angular total do sistema ao passar pelo ponto B.
Questão 98
A figura a seguir mostra um dispositivo utilizado para puxar uma esfera oca de raio e massa rolando sem deslizar ao longo de um plano com inclinação em relação à horizontal. A esfera é puxada da base do plano inclinado a partir do repouso por uma roldana (disco sólido) de raio e massa pela aplicação de uma força constante na direção tangente à posição de uma manivela (comprimento e massa desprezível) fixada em um eixo que passa no centro de massa da roldana, conforme mostra a vista frontal do dispositivo. Adote , despreze os efeitos de atrito no eixo da roldana e considere o fio ideal.
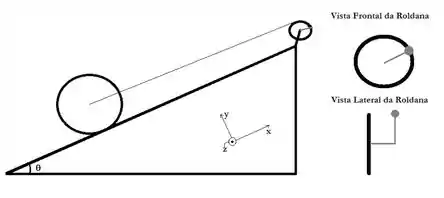
A força é tal que suspende a esfera oca ao longo da rampa com uma aceleração de centro
de massa constante .
Determine a energia cinética da esfera oca dois segundos após o início do movimento.
Determine o vetor momento angular final da esfera oca, em relação ao seu centro de massa, dois segundos após o início do movimento.
Faça o diagrama do corpo livre para a esfera oca e para a roldana e escreva as equações que regem os movimentos destes corpos.
Obtenha o módulo da força aplicada à manivela.
Ver solução completaQuestão 99
Uma partícula de massa descreve uma trajetória na forma de uma circunferência de raio . Sua posição angular (em rad.) e dada pela expressão:
Com o tempo em segundos.
O módulo do momento angular da partícula (em ) em relação ao centro da circunferência no instante vale:
Questão 100
Uma correia ideal liga dois discos homogêneos de raios idênticos a e massas e , cuja distância entre os seus centros é . Os seus centros estão fixos por pinos em torno dos quais cada disco pode girar sem atrito. Uma correia tensa e inextensível passa pelas periferias dos discos, sem deslizar sobre elas, e move-se com velocidade de módulo constante , como indica a figura.
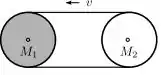
Sabendo-se que o momento de inércia de um disco homogêneo de massa e raio para um eixo que passa pelo seu centro e perpendicular a sua superfície é , podemos afirmar para o módulo do momento angular total do sistema constituído pelos discos, relativo ao seu centro de massa, que
Questão 101
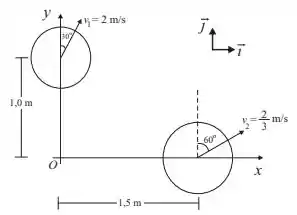
Dois objetos estão se movendo como mostra a figura ao lado. O objeto de massa move-se com vetor velocidade que faz um ângulo de com o eixo . O objeto de massa move-se com vetor velocidade que faz um ângulo de com o eixo . O valor do momento angular total em torno do ponto O é (no SI):
Questão 102
Uma bola 1 de raio desprezível e massa encontra-se suspensa na extremidade de um fio inextensível, de massa desprezível e comprimento . Ela é atingida por uma bola 2,também de raio desprezível, de massa que desloca-se com velocidade , sobre uma canaleta horizontal, cuja extremidade encontra-se na posição da bola 1, como ilustrado na figura. A colisão é elástica.
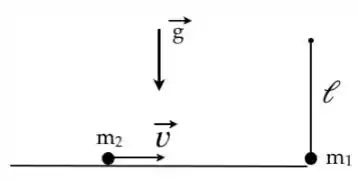
(a) Determine os vetores velocidade das bolas imediatamente após a colisão.
(b) Determine o vetor velocidade da bola 1 no topo da trajetória.
(c) Calcule a tensão no fio quando a bola 1 está no topo da trajetória.
(d) Calcule o vetor momento angular do sistema em relação ao ponto de suspensão da bola 1 antes e imediatamente após a colisão.
Ver solução completaQuestão 103
Uma haste metálica delgada, de comprimento e massa , pode girar livremente em torno de um eixo horizontal, que a atravessa perpendicularmente, à distância de uma extremidade. A haste é solta a partir do repouso, na posição horizontal.
(a) Calcule o momento de inércia da haste, com respeito ao eixo em torno da qual ela gira.
(b) Calcule a velocidade angular adquirida pela haste após ter caido de um ângulo , bem como a aceleração .
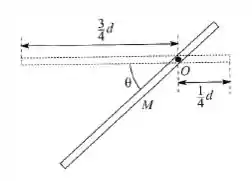
Questão 104
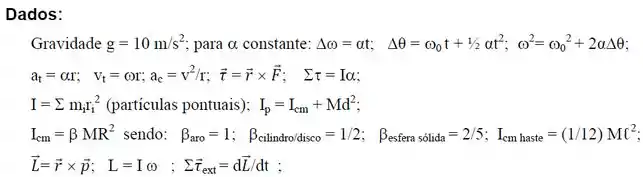
Uma esfera de massa 4,0 𝑘𝑔 e um cubo de massa 2,0 𝑘𝑔 estão conectados por uma corda inextensível e de massa de desprezível. A corda passa por uma roldana de raio 1,0 𝑚 e massa 2,0 𝑘𝑔 que tem a forma de um disco como ilustrado esquematicamente na figura ao lado. Ambos os corpos estão com velocidade de módulo igual a 𝑣 (𝑚/𝑠). Calcule em o módulo do momento angular do sistema em relação ao centro da roldana.
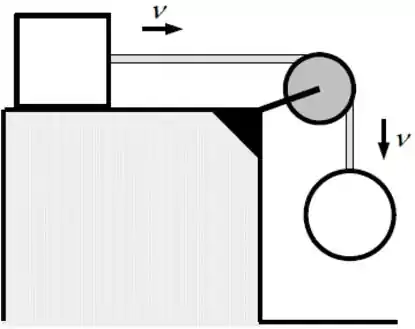
(a)
(b)
(c) 7
(d)
(e)
Ver solução completaQuestão 105
Uma barra de massa e comprimento roda livremente em um eixo localizado em uma de suas laterais. A barra é solta da posição horizontal. Qual a aceleração angular quando a barra faz um ângulo de 30º com a vertical.
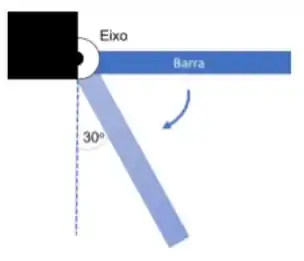
a) 2g/(3L)
b) g/(3L)
c) 3g/(4L)
d) 3g/(2L)
e) g/L
Ver solução completaQuestão 106
Se o vetor momento angular de uma partícula é constante, é incorreto dizer:
A. Que o torque total sobre a partícula é sempre nulo.
B. Que os vetores posição e momento linear da partícula mantém-se num plano perpendicular ao vetor momento angular.
C. Que a área varrida pela trajetória é constante quando a partícula está sob ação de uma força central atrativa.
D. Que a força total sobre a partícula é sempre nula.
E. Que tem uma resposta acima incorreta
Ver solução completaQuestão 107
44. Um sistema formado por dois baldes e uma barra estão fixados a um eixo como indicado na figura. O sistema, que gira em torno do eixo com uma certa velocidade angular, descreve um círculo no plano perpendicular ao eixo. De repente começa a chover. Despreze qualquer tipo de atrito e força de resistência. Pode-se afirmar que:
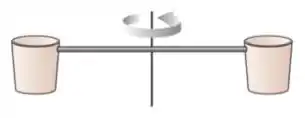
(a) Os baldes continuam girando com a mesma velocidade angular constante como consequência da conservação do momento angular do sistema baldes+barra+chuva.
(b) Os baldes giram com maior velocidade angular porque o momento angular do sistema baldes+barra é conservado.
(c) Os baldes giram com menor velocidade angular como consequência da conservação do momento angular e da energia mecânica do sistema baldes+barra+chuva.
(d) Os baldes giram com menor velocidade angular porque o momento angular do sistema baldes+barra+chuva é conservado.
Ver solução completa