Um grande aquário de de altura está cheio de água doce até uma altura de . Uma das paredes do aquário é feita de plástico e tem de largura. De quanto aumenta a força exercida sobre a parede se a altura da água é aumentada para ?
Passo 1
Show de bolinhas pessoal, primeira coisa a gente tem que lembrar que a pressão de um fluido em repouso varia (entre dois pontos e no interior de um fluido de densidade ) de acordo com a posição vertical:

Passo 2
Considerando os pontos e como localizados a uma profundidade e (sobre a superfície do líquido), respectivamente, temos que a pressão em um ponto qualquer é dada por :
Onde o aquário pode ser desenhado como:
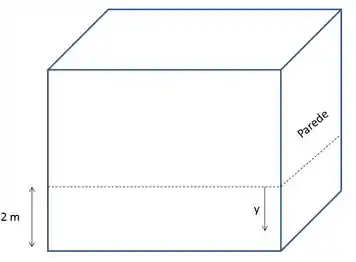
Como a pressão atmosférica atua tanto no interior do líquido quanto na região externa à parede, para efeitos de cálculo da pressão exercida pelo fluido na parede, consideramos apenas a pressão manométrica, tal que:

Passo 3
Uma das formas de calcular a forca exercida pelo fluido sobre a parece vertical indicada na figura é através da soma das componentes de força exercidas pela ação da pressão do líquido nas diversas unidades de área que compõem a superfície da parede, até uma altura de
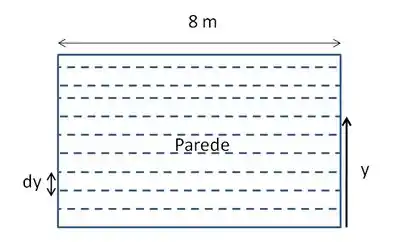
Nesse caso, a força em cada unidade de área é dada por :
Como podemos perceber na Figura, cada unidade de área vale:
Logo, as forças exercidas pelo líquido em cada componente de área da parede são expressas assim:
Passo 4
O somatório das infinitas forças que fornece o valor da força total exercida pelo fluido sobre a parede, é dado pela integral da expressão acima
Lembre-se que:
Dessa forma, sendo a altura do fluido, obtemos que:
Passo 5
A partir disso, podemos calcular o aumento de força decorrente do aumento do nível de água contido no aquário:
