Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 19.1 - Ex. 78
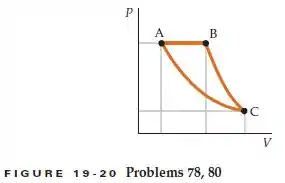
Em uma máquina térmica, 2,00 mols de um gás diatômico são conduzidos pelo ciclo ABCA, como mostrado na Figura 19-20. (O diagrama PV não está desenhado em escala). Em A, a pressão e a temperatura são 5,00 atm e 600 K. O volume em B é o dobro do volume em A. O segmento BC é uma expansão adiabática e o segmento CA é uma compressão isotérmica.
- Qual é o volume do gás em A?
- Quais é o volume e a temperatura do gás em B?
- Qual é a temperatura do gás em C?
- Qual é o volume do gás em C?
- Quanto trabalho é feito pelo gás em cada um dos três segmentos do ciclo?
- Quanto calor é absorvido ou liberado pelo gás em cada segmento deste ciclo?
Passo 1
a) Olá! Tudo bem? A gente tem um ciclo e ele pede para gente achar algumas informações sobre ele. Vamos usar também fórmulinhas dos capítulos anteriores aqui, tá bem?
Muito bem, a primeira coisa aqui é achar o volume do gás em A. Para um gás ideal usamos a fórmula:
O enunciado diz que em A, temos que
Precisamos passar a pressão para porque estamos usando joules, tá? Substituímos:
Transformando para litros
Passo 2
b) Próxima pergunta, qual é o volume e a temperatura do gás em B. Ele diz que o volume em B é o dobro do volume em A, então:
Em litros:
Quanto a temperatura, podemos usar a lei para os gases para esse ponto
Lembrando que pelo diagrama, a pressão em A é igual a pressão em B
Substituindo:
Passo 3
c) O que queremos? A temperatura em C.
A gente tem que a curva CA é uma compressão isotérmica. Isso significa que todos os pontos dessa curva têm a mesma temperatura. Inclusive C e A!
Como a gente sabe a temperatura em A, a em C é:
Passo 4
d) E vamos seguindo! E agora? Devemos achar o volume em C.
Como o segmento BC é adiabático, temos que para todos os pontos desse segmento, vale que:
Então vale usar a seguinte relação entre os pontos B e C:
Onde:
Sabendo que para um gás diatômico (nosso tipo de gás) e :
Assim:
E nossa expressão fica:
Isolando o volume:
Substituindo:
Em litros:
Passo 5
e) Agora vamos para o trabalho. No segmento AB, expansão à pressão constante, o trabalho é calculado como:
Colocando os valores:
No segmento BC, expansão adiabática, o trabalho é dado por:
Lembrando que
Substituímos:
Esse é o trabalho sobre o gás. Então o trabalho realizado pelo gás vai ter sinal trocado
E vamos finalizar os trabalhos achando o segmento CA, compressão isotérmica. O trabalho realizado pelo gás é calculado como:
Colocando os valores:
Essa é grande, né? E ainda não acabou.
Passo 6
f) Para terminar a questão nos falta achar o calor para cada etapa. À pressão constante no trecho AB temos a seguinte relação que envolve o calor:
Vimos que para um gás diatômico e , então
Assim para o trecho AB
Substituindo:
No processo adiabático BC não há troca de calor, então:
E, por último, temos um processo isotérmico. Ou seja, não há variação de temperatura. Quando a temperatura não varia não há variação de energia interna do gás:
Pela primeira lei da termodinâmica:
Como a variação de energia é nula:
Lembrando que o trabalho realizado sobre o gás tem sinal inverso ao trabalho realizado pelo gás:
Substituindo:
Então:
Terminamos!