Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 18.Problemas Adicionais - Ex. 78
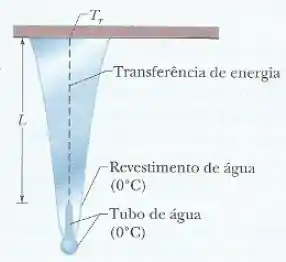
Pingentes de gelo. A água cobre a superfície de um pingente de gelo ativo (em processo de crescimento) e forma um tubo curto e estreito na extremidade do eixo central (Figura). Como a temperatura da interface água-gelo é , a água do tubo não pode perder energia para os lados do pingente ou para a ponta do tubo porque não há variação de temperatura nessas direções, A água pode perder energia e congelar apenas transferindo energia para cima (através de uma distância ) até o alto do pingente, onde a temperatura , pode ser menor que . Suponha que e . Suponha também que a seção reta do tubo e do pingente é . Qual é, em termos de , (a) a taxa com a qual a energia é transferida para cima e (b) a taxa com a qual a massa é convertida de água para gelo no alto do tubo central? (c) Qual é a velocidade com a qual o pingente se move para baixo por causa do congelamento da água? A condutividade térmica do gelo é e a massa específica da água é .
Passo 1
(a) Beleza, a situação pode parecer meio complicada, mas se a gente for direto ao ponto dá tudo certo, quer ver?
A questão pediu a taxa com a qual a energia é transferida para cima. Qual é a fórmula da taxa de transferência de energia (na forma de calor)?
A condutividade térmica , o a altura do pingente já foram dadas no enunciado. Além disso, a questão quer a resposta em termos de , então não precisamos achar um valor pra ele.
E a diferença de temperatura? Isso também foi dado. A temperatura é na extremidade de baixo, e na base do pingente.
Então tá, vamos substituir isso tudo:
O que é aproximadamente:
Passo 2
(b) Agora que a gente já sabe a taxa com que o calor flui pra cima, fica tranquilo descobrir a taxa com que água é convertida de água pra gelo.
Se a taxa de transferência de calor é , isso quer dizer que são transferidos joules a cada segundo.
Só que a gente precisa fazer é descobrir quanta água dá pra congelar com joules, e essa vai ser a quantidade congelada a cada segundo!
Pronto, essa é a massa de água que é congelada a cada segundo!
Resolvido!
Passo 3
Agora vamos pensar o seguinte: conforme mais água vai sendo congelada, o pingente de gelo vai ficando mais comprido, concorda?
A ideia é calcular a velocidade do aumento da altura do pingente, supondo que a área da seção reta dele seja .
A gente já viu que a massa de água ali aumenta nessa taxa aqui:
Como a gente pode relacionar isso com a altura do pingente? Vamos pensar na fórmula da massa específica:
Se a gente derivar isso em relação ao tempo:
Como a massa específica da água é constante, aquela derivada ali só afeta o volume:
E a fórmula do volume (aproximando a ponta do pingente como um cilindro) é:
E como esse também é constante, a derivada do só vai “afetar” o :
Ótimo, esse é exatamente o que a gente quer calcular!
Passo 4
(c) Vamos começar isolando o que a gente quer achar:
Pronto, essa é a resposta da letra (c).
Resposta
(a) .
(b) .
(c) .