Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.Problemas - Ex. 89
Um pintor está em pé em um andaime que é içado a uma velocidade escalar constante. Na subida, ele acidentalmente derruba uma lata de tinta do andaime e ela despenca até o chão. Você está observando a cena e mede com o seu cronômetro que leva para a lata atingir o solo. Despreze a resistência do ar. a) Qual é a velocidade escalar da lata quando ela chega ao solo? b) Outro pintor está parado no peitoril com as mãos acima do ponto da queda da lata. Ele tem reflexos rápidos e, se a lata passar por ele, poderá apanhá-la. Existe essa chance?
Passo 1
Oi, galerinha! Tudo bom? Yuri aqui e estarei te ajudando a resolver essa atividade.
Repara que temos uma problema sobre a queda livre de uma lata de tinta.
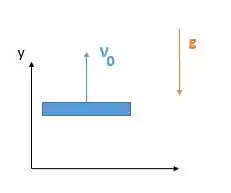
Mas repara, que lata estava sendo içada, então vamos tomar como para cima. A velocidade inicial positiva pode ser igual à velocidade positiva do andaime. Além disso, conforme ela cai, a lata tem aceleração constante, .
Passo 2
- Então, primeiro vamos encontrar velocidade escalar da lata quando ela chega ao solo:
- Vamos encontrar a altura máxima da lata, acima do ponto em que ela cai do andaime.
Mas antes temos que achar a velocidade inical da lata. Então vamos usar a equação:
variação de altura
variação da velocidade inicial
tempo
aceleração
Substituindo os valores que nós já sabemos:
Então:
Passo 3
Usando , vamos encontrar a velocidade final quando a lata chega ao solo através da equação:
Substituindo os valores que conhecemos:
Logo o resultado da velocidade final é igual a:
Repara que a velocidade é negativa, pois ela está no sentido contrario ao içamento, ou seja, para baixo.
Passo 4
Vamos entender uma coisa, antes da lata cair como ela tinha uma velocidade positiva direcionada para cima, ela continua subindo até começar a cair. Mas quando isso ocorre?
Ela começa a subir com uma velocidade de até que atinge uma altura e velocidade igual a zero e começa a cair. Queremos saber qual é essa altura que ela atinge antes de começar a cair.
Como aqui não nos pede e não precisamos calcular o tempo, vamos utilizar a equação de Torricelli:
Substituindo os valores que já conhecemos:
Logo:
Como o outro pintor está a uma altura de 4,0m acima do andaime e a lata atinge 6,53m de altura antes de começar a cair, concorda comigo que a lata passará por ele e ele conseguirá pegar? Então, sim, ele tem uma chance.
Resposta
- Sim.