Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 19
Uma prancha gravitacional é uma maneira conveniente e rápida de se determinar a localização do centro de gravidade de uma pessoa. Ela consiste em uma prancha horizontal suportada por um fulcro em uma extremidade e uma balança de mola na outra. Para uma demonstração em aula, seu professor de física pede que você deite sobre a prancha com o topo de sua cabeça extremamente sobre o fulcro, como mostrado na Figura 12-33. O fulcro está a da balança. Preparando este experimento, você se pesou previamente, com precisão, e verificou que sua massa é de . Quando você está sobre a prancha gravitacional, o ponteiro da balança adianta além do ponto que indicava quando só a prancha estava sobre ela. Use estes dados para representar a localização de seu centro de massa em relação a seus pés.
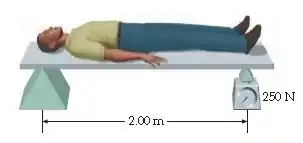
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Ele pede para acharmos o centro de massa da pessoa que está deitada. Podemos pensar que a pessoa e a prancha gravitacional formam um corpo rígido que está apoiado em suas duas extremidades, uma pelo fulcro e outra pela balança.
Ambos os apoios geram reações nesse corpo rígido, que podemos considerar que estão orientadas para cima. E podemos entender que esse corpo rígido sofre ação da força peso da pessoa.
Nessas questões com forças e reações é importante fazer um diagrama de corpo livre do sistema. Então vamos fazer o nosso! Nas extremidades temos as forças de reação. E temos a força peso. Mas onde essa força é exercida? No centro de massa da pessoa! Temos o diagrama:
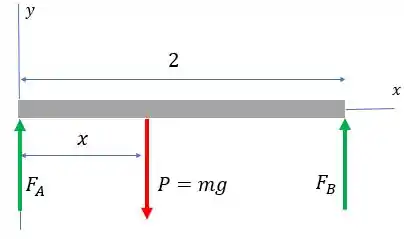
Percebe que a gente posicionou a força peso em uma posição genérica , isso porque ela está no centro de massa do corpo, e a gente não sabe ainda onde ele está.
Como nessa situação tudo está paradinho, a gente pode usar as equações de equilíbrio
Para achar o valor de . Vamos lá!
Passo 2
Vamos reunir nossos dados. O enunciado diz que a massa da pessoa é de . Então a força peso é
E ele disse que depois que a pessoa está sobre a prancha, a balança registra . Isso é um jeito criativo de dizer que no apoio representado pela balança a força vale
Então, olhando para o nosso diagrama, quais são as nossas incógnitas? É a posição do centroide e o valor da força no apoio da esquerda .
Mas a gente só quer , né? Então a gente pode usar a equação de equilíbrio do Torque.
Se a gente calcular o Torque resultante na extremidade esquerda do corpo, nós podemos desconsiderar a força porque ela não gera momento nesse ponto, já que é onde ela está aplicada.
Passo 3
Aplicando , considerando o sentido anti-horário positivo, temos:
Vamos entender essa equação. é o torque gerado pela força , como ele tende a girar a peça no sentido anti-horário, ele fica positivo. E a distância entre o ponto onde queremos o torque (a extremidade esquerda) e linha de ação da força é , por isso aparece aquele 2.
Já é o torque gerado por . Essa força tende a gerar o elemento no sentido horário, por isso fica negativa. E a distância do ponto de aplicação da força até a extremidade esquerda do corpo é .
Isolando , quem a gente queria encontrar, temos
Substituindo os valores, temos: