Um laboratório de biologia de sua universidade esta estudando a localização do centro de gravidade de uma pessoa em função do seu peso. Eles pagam bem e você se oferece voluntario. A localização do seu centro de massa, quando de pé, deve ser determinada fazendo você deitar em uma plataforma homogênea (massa de , compriemtno de ) apoiada sobre duas balanças de mola, como mostrado na Figura 12-48. Se sua altura é e a balança da esquerda indica , enquanto a balança da direita indica , onde está seu centro de gravidade em relação aos seus pés? Suponha que as balanças, separadas por , estejam exatamente à mesma distância das duas extremidades da prancha e zeradas antes de você deitar na prancha.
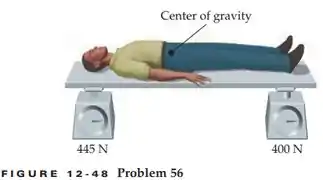
Passo 1
Como nossa temo muita informação, vamos fazer uma ilustração. Se liga só:
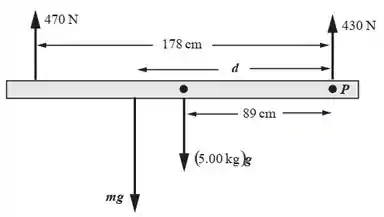
Agora tá dando pra entender um pouco melhor 😊
Passo 2
Como não temos a massa , vamos usar que . Logo,
Assim,
Portanto,
Como queremos saber a distancia podemos fazer torque com relação ao ponto . Repare que , pois nosso sistema está em equilíbro. Consideramos sentido horário positivo, temos:
Passo 3
Vamos arrumar as coisas pra gente não se confundir. Como e :
Isolando :
Fazendo as contas: