Segundo o modelo da partícula do núcleo, o é formado por por 3 partículas , ou seja, por três núcleos de . Analogamente o é formado por quatro partículas .
(a) Use a tabela 15-1 para calcular a diferença entre as energias de ligação total do e as três partículas .
(b) Calcule a diferença entre as energias de ligação totais do e das quatro partículas .
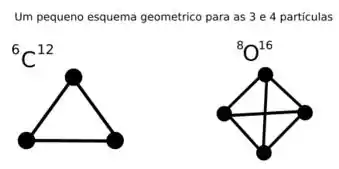
(c) Desenhe um diagrama esquemático de e segundo o modelo de partículas e use-os para mostrar que pode existir 3 “ligações” entre as partículas no enquanto podem existir 6 ligações entre as partículas no . A natureza exata dessa ligação não é especificada no modelo mas pensou-se que elas fossem análogas às que ligam as moléculas.
(d) Utilize os resultados dos itens (a) e (b) para mostrar que as energias de ligações totais do e podem ser obtidas considerando que cada ligação possível contribui com uma energia de ligação ligeiramente superior a 2 MeV. O modelo da partícula não é profundamente utilizado porque pouca coisa a mais pode ser feita além do que já foi feito neste problema.
Passo 1
Bem semelhante ao problema 14, vamos encontrar as energias de ligação para e para .
]
A diferença entre a energia de ligação de e suas três partículas é respectivamente:
Esse é o valor correspondente à diferença de energia de ligação e das partículas para o item (a).
O mesmo acontece para o caso do , iremos usar a mesma abordagem mas desta vez, temos 4 partículas . Então mãos à obra!
Nossa diferença de energia vai ser da forma:
Passo 2
O número de ligações é dado pela seguinte equação:
Para o caso do , N= número de partículas . Assim
,
o mesmo ocorre para N=4
.
Assim temos que o número de ligações para os casos e são respectivamente 3 e 6.
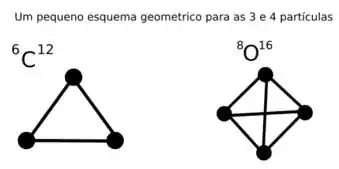
Passo 3
Para o ítem (d), O que ele nos pede é uma relação da nossa energia ligação com as ligações de cada partícula . Então para e teremos respectivamente
o que nos dá valores de energia superior a 2 MeV.
Resposta
Por fim, nossas respectivas respostas para os itens (a), (b), (c) e (d) são:
(a)
(b)
(c) ; .
(d) .