Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 5.Exercícios e Problemas - Ex. 18
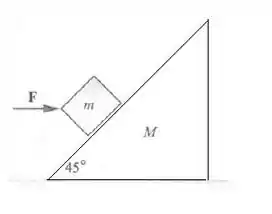
Suponha que o atrito do bloco de seção triangular da Figura 5.17 com o piso e com o paralelepípedo seja nulo. Calcule a aceleração do bloco de seção triangular e do paralelepípedo.
Passo 1
Oi pessoas, tudo certo com vocês? Espero que sim 😊. Nessa questão vamos entender mais sobre plano inclinado.
Primeiro vamos colocar as forças que atuam sobre o bloco. Note que podemos representar assim:
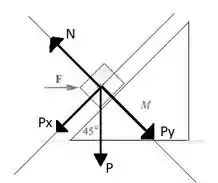
Observe que,
Passo 2
Certo! Sabendo disso, vamos aplicar as equações do peso e da força resultado, logo, teremos que
Como,
Temos:
Resposta
Exercícios de Livros Relacionados
Duas ligas de borracha idênticas fazem conjuntamente um objeto acelerar com aceleração a . Quantas ligas de borracha dessas são necessárias para fazer um objeto com a metade da massa acelerar três vez
Para um objeto que parte do repouso e acelera uniformemente, a distância percorrida é proporcional ao quadrado do tempo transcorrido. Se um objeto percorre 400 m nos primeiros 2 s , que distância ele
A figura E x . 5.9 mostra o gráfico da aceleração versus força para dois objetos puxados por ligas de borracha. Qual é a razão m 1 / m 2 ?
E x . 5.8 mostra o gráfico da aceleração versus força para três objetos puxados por ligas de borracha. A massa do objeto 2 é 0,2 k g . Quais são as massas dos objetos 1 e 3 ? Explique seu raciocínio.
Um caixote contendo pratos delicados encontra-se na carroceria de um pequeno caminhão. Partindo de um semáforo, o veículo acelera para o norte, e o caixote se move sem escorregar. A força de atrito pa