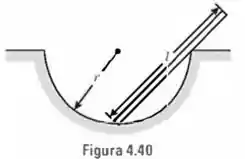
Uma vara de massa e comprimento (Fig. 4.40) é colocada num hemisfério de raio completamente sem atrito. Determine a posição de equilíbrio da vara. Calcule as reações do hemisfério sobre a vara. Discuta as soluções correspondentes a e .
Passo 1
E aí, beleza?? Primeiramente, vamos analisar o caso . Nesse caso, a barra fica totalmente dentro do hemisfério e as reações normais em suas extremidades apontam para o centro deste, e cruzando nesse ponto. Pelo teorema das três forças, demonstrado em um dos exercícios deste capítulo, sabemos que em um sistema estático submetido a três forças, elas devem se encontrar em um único ponto. Assim, concluímos que a força peso também deve ter sua linha de ação passando pelo centro do hemisfério. Portanto, a única situação de equilíbrio possível é quando a barra está na horizontal, de maneira simétrica, como na figura a seguir:
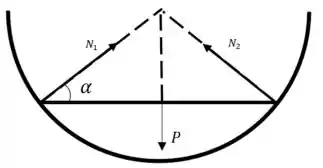
Assim, as reações são iguais e valem:
Portanto:
Passo 2
Agora para o caso , uma das extremidades da barra fica para fora do hemisfério. Considere a seguinte ilustração:
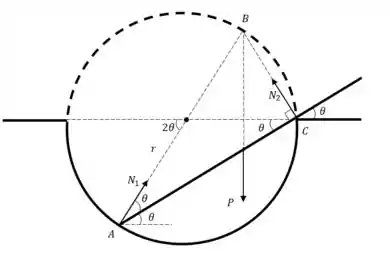
Da geometria do problema, temos que as três forças se cruzam em um único ponto () e esse ponto está sobre a circunferência, uma vez que a força é perpendicular à barra. O ângulo vale pois é ângulo central. Note, portanto, que as projeções horizontais de e são iguais, com isso:
Passo 3
Assim, vem:
Resolvendo a equação, vem:
Portanto, como ficamos com a solução positiva, vem:
Passo 4
Para , podemos escrever a equação do torque em relação ao ponto :
Escrevendo o equilíbrio rotacional agora, em torno do ponto , vem:
Resposta
(a)
(b)