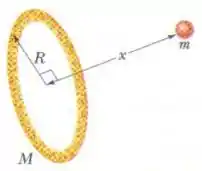
Vários planetas (Júpiter, Saturno, Urano) possuem anéis, talvez formados por fragmentos que não chegaram a formar um satélite. Muitas galáxias também contêm estruturas em forma de anéis. Considere um anel fino homogêneo de massa e raio externo . (Veja a figura). (a) Qual é a atração gravitacional que o anel exerce sobre uma partícula de massa localizada no eixo central do anel a uma distância do centro do anel? (b) Suponha que a partícula do item (a) seja liberada a partir do repouso. Com que velocidade ela passa pelo centro do anel?

Agora vamos pensar na distância entre a massa e um ponto qualquer do anel:

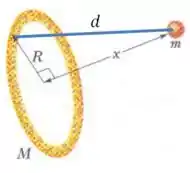
Pelo Teorema de Pitágoras, podemos escrever o seguinte:

E perceba que essa distância é a mesma para todos os pontos do anel, que tem massa total , então podemos escrever a expressão para da seguinte forma:

E podemos derivar essa expressão para encontrar o módulo da força gravitacional:

Precisamos aplicar a regra da cadeia para resolver essa derivada:

Mas isso não resolve nosso problema , porque a força precisa de uma direção e um sentido. Perceba que para cada ponto no anel circular, existe outro ponto na exata direção oposta:

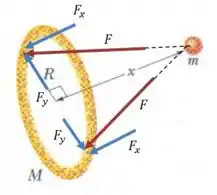
Então, em cada um desses pares, podemos ver que todas as componentes da força na direção vertical vão se cancelar, enquanto as horizontais vão se somar.

Então a força resultante sobre a partícula vai apontar na direção do centro do anel, ao longo do eixo .

(b) Agora queremos calcular a velocidade da partícula quando ela chega até o centro do anel. Vamos pensar em termos de conservação de energia:

Inicialmente, a partícula está parada ( e tem a energia potencial que calculamos no passo :

E quando chega até o centro do anel (), a energia potencial será dada por:

E a energia cinética será:

Então:

Podemos usar isso para calcular a velocidade:

Agora é só isolar: