Uma bola gira no sentido anti-horário em um círculo vertical na ponta de uma corda de de comprimento. Quando a bola passa a do ponto mais baixo em seu caminho para cima, sua aceleração total é . Para esse instante, (a) desenhe um diagrama vetorial mostrando as componentes de sua aceleração, (b) determine o módulo de sua aceleração radial e (c) determine a velocidade escalar e a velocidade da bola.
Passo 1
E aiii gente, tudo bom com vocês?
Vamos fazer mais uma questãozinha aqui?
Vem comigo!
Letra a:
Ver figura abaixo:
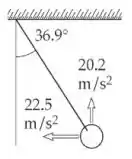
Passo 2
Letra b:
A posição da bola está a do ponto mais baixo no caminho para cima, ou seja, o vetor posição forma um ângulo de com a vertical para cima.
Como a aceleração radial aponta na direção contrária à posição, ela faz o mesmo ângulo, mas para o centro do círculo.
Portanto, o vetor unitário que aponta para o centro é:
Substituindo valores:
Sabendo que a aceleração radial é na direção do centro, temos:
Agora, vamos projetar a aceleração total sobre a direção radial para encontrar seu módulo:
Passo 3
Letra c:
Sabemos que:
Então:
Agora, a direção do vetor velocidade é tangente ao círculo, ou seja, perpendicular ao vetor radial.
Como a bola está subindo no sentido anti-horário, a tangente aponta perpendicularmente para a esquerda (ou seja, 90° à esquerda da direção do raio).
Se o vetor radial é:
Então o vetor tangente (perpendicular, sentido anti-horário) será:
Portanto, o vetor velocidade é:
Resposta
- Ver figura
- e .