Rotação de Corpos Rígidos
Produzido por Pablo RicardoTeoria
Introdução
Você certamente já andou de bicicleta ou pelo menos viu alguém andando, né?

Mas você já parou para pensar em como uma bicicleta funciona? Existe uma engrenagem ligada ao pedal e outra engrenagem ligada à primeira por meio de uma corrente.
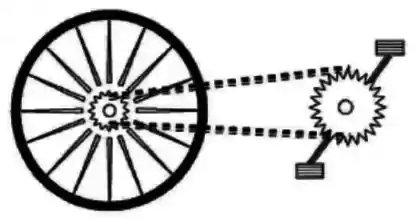
Quando você pedala, a primeira engrenagem entra em movimento e através da corrente ocorre a transferência de movimento para a segunda engrenagem, que por sua vez está ligada a roda da bicicleta fazendo-a andar.
O movimento de engrenagens é o que faz muitas máquinas funcionarem, por isso é importante sabermos como funciona o movimento dos corpos. É isso que vamos aprender neste capítulo. Partiu?
Movimento do Corpo Rígido
Nós aprendemos até aqui sobre o deslocamento, velocidade e aceleração de pontos que se deslocam em uma reta ou curva.
Para o corpo rígido vamos usar essas mesmas relações, mas temos que levar em conta o movimento rotacional do corpo. Ou seja, para analisar o movimento de um corpo rígido, temos que considerar também o deslocamento, a velocidade e a aceleração que vamos chamar de angulares.
Rotação
O nosso corpo rígido vai ter rotação quando ele girar em torno de um ponto fixo. Quando isto acontece, dizemos que qualquer ponto desse corpo tem movimento circular.
Imagine este disco girando em torno do ponto fixo em seu centro:
Repare que o ponto , que pertence ao corpo, realiza um movimento circular. Mas para entender o movimento do ponto temos que entender primeiro o movimento que o corpo, neste caso o nosso disco, faz em torno do ponto em que está girando.
O nome do movimento que o corpo faz é movimento angular. Uma partícula não apresenta movimento angular, pois consideramos que ela não tem dimensões. Já linhas e corpos rígidos podem apresentar este movimento. Então, vamos entender esse tal de movimento angular direitinho.
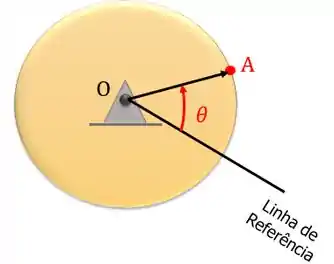
- Posição Angular: para localizar um ponto com relação a um referencial usávamos vetores. Agora, vamos usar um ângulo medido a partir de uma linha de referência fixa:
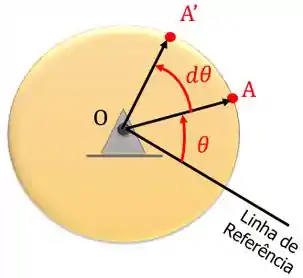
- Deslocamento Angular: é a mudança da posição que ocorre por causa da rotação do corpo. Ou seja, o nosso disco gira e o ponto passa para outra posição . Vamos medir esta grandeza como um vetor infinitesimal .
- Velocidade Angular: esta grandeza mede o quanto a posição angular varia no tempo. Como a variação da posição angular é bem pequenininha, temos que pegar intervalos de tempo bem pequenos também (). Então, a nossa velocidade angular, que chamaremos de , será:
-
Aceleração Angular: esta grandeza mede o quanto a velocidade varia no tempo. Para isso, vamos considerar variações de velocidade angular bem pequenas () e intervalas de tempo igualmente pequenos (). Então, a aceleração angular, que chamaremos de , será:
Podemos dizer também que a aceleração angular é a derivada segunda do deslocamento angular com relação ao tempo:
A direção da aceleração angular é a mesma direção da velocidade angular . Maaas, o seu sentido depende se a velocidade angular aumenta ou diminui:
- Se a velocidade angular cresce, então a aceleração angular tem o mesmo sentido de ;
- Se a velocidade angular diminui, então a aceleração angular tem sentido oposto de e é chamada de desaceleração angular.
- Relação entre aceleração angular, velocidade angular e deslocamento angular: se isolar a variação de tempo nas equações da velocidade angular e da aceleração angular , teremos:
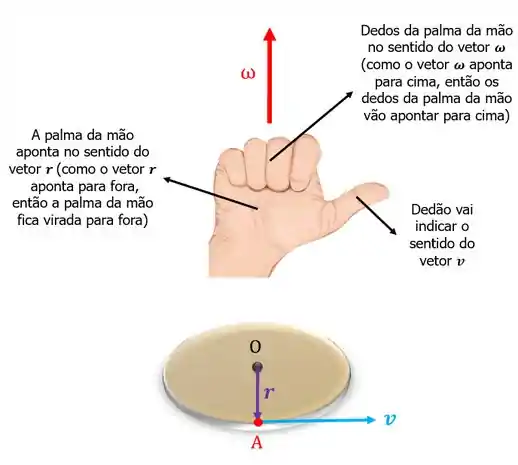
Para determinar o sentido do vetor , vamos utilizar a regra da mão direita. Para isso, colocamos os dedos da mão direita no sentido em que o disco está rodando e vemos se o polegar vai apontar para cima ou para baixo.
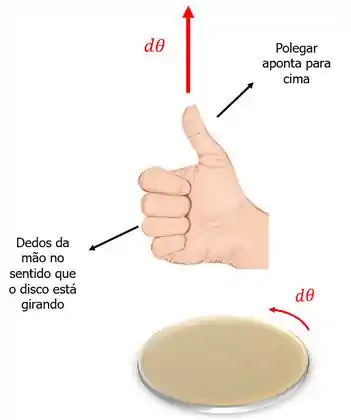
Se o disco estivesse girando no sentido horário teríamos:
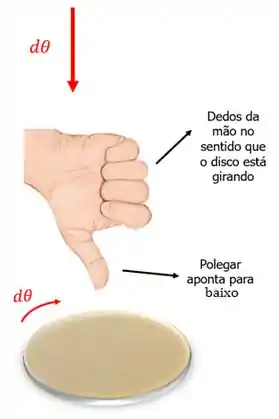
Vamos arbitrar como positivo quando o polegar apontar para cima, ou seja, quando o disco estiver girando no sentido anti-horário. Beleza?
A velocidade angular é um vetor que terá a mesma direção que o vetor . A sua unidade mais usual é em O sentido da velocidade angular também é determinado pela regra da mão direita, do mesmo jeito que anteriormente. Então, o sentido positivo que escolhemos será:

Agora vamos igualar estas equações e separar as variáveis:
Guarde esta equação, ela é muito semelhante com aquela que tínhamos para movimento retilíneo!
Aceleração Angular Constante
Se a aceleração angular do corpo for constante e integrarmos a equação da aceleração angular, teremos:
Se considerar o tempo inicial como zero, vamos obter a seguinte equação:
Ou seja, quando a aceleração angular é constante, as equações que vimos até agora, quando integradas, resultam em um conjunto de equações que nos será muito útil.
Onde, é a velocidade angular inicial e é o deslocamento angular inicial.
Movimento de um Ponto pertencente ao Corpo
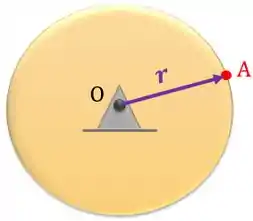
Conforme o corpo rígido gira, qualquer ponto que pertence ao corpo vai girar junto, não é? Então, o ponto que pertence ao disco se desloca fazendo uma trajetória circular de raio e centro no ponto .
- Posição: a posição de qualquer ponto que pertence ao corpo é determinada por um vetor que tem origem no ponto em torno do qual o corpo gira (no nosso caso, o ponto ) e chega até o ponto que estamos analisando:
- Velocidade: se analisarmos a velocidade usando coordenadas polares, ela terá uma componente radial e uma componente tangencial :
- Aceleração: a aceleração terá uma componente tangencial e outra perpendicular à trajetória que é a aceleração normal :
Repare que o raio não varia com o passar do tempo, então a componente radial é zero (). Repare também que:
Então, vamos substituir por na componente tangencial da velocidade:
Dessa maneira, a velocidade de um ponto que pertence ao corpo será:
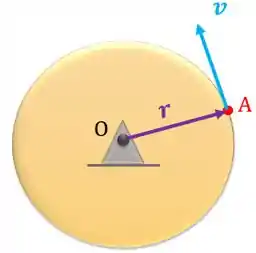
Repare que o vetor é sempre tangente à trajetória.
Podemos determinar o vetor velocidade usando produto vetorial:
O sentido do vetor v pode ser determinado pela regra da mão direita também:
A aceleração tangencial indica o quanto a velocidade varia no tempo. E quanto ao seu sentido?
- Se a velocidade está diminuindo, o vetor aceleração tangencial terá sentido contrário ao vetor ;
- E se a velocidade está aumentando, o vetor aceleração tangencial terá o mesmo sentido do vetor .
Podemos calcular a aceleração tangencial por produto vetorial também:
A aceleração normal indica o quanto a velocidade muda de direção ao longo do tempo. O vetor aceleração normal sempre aponta para o ponto em torno do qual o corpo está girando.
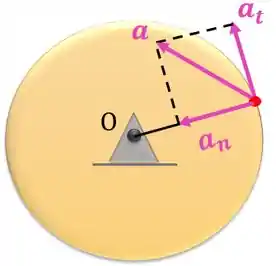
Desse modo, a aceleração será:
Transmissão de Movimento
Imagine duas polias unidas por uma corda:
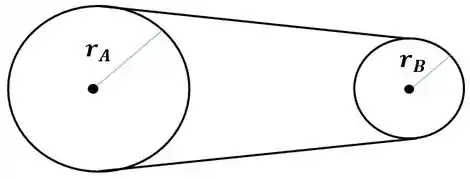
A polia tem um raio e a polia tem um raio . Se a polia começar a girar, a polia também irá se movimentar, pois tem uma corda unindo as duas. Mas qual a relação entre o movimento que elas realizam?
Imagine que antes de começar o movimento, pegamos uma canetinha e marcamos um ponto na primeira polia e um ponto na segunda.
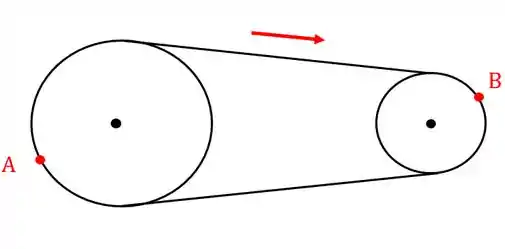
Após um intervalo de tempo de tempo esses pontos vão mudar de posição, não é mesmo? O ponto vai passar para uma posição e o ponto vai para uma posição :
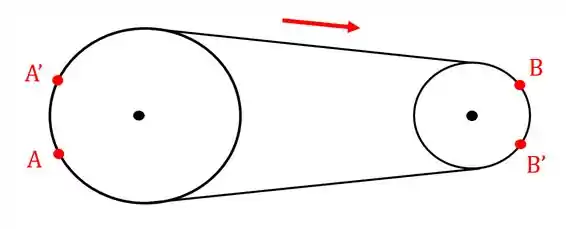
Repare que se considerarmos que a corda não escorrega, o tanto que a corda andou na polia é o mesmo tanto que ela andou na polia , ou seja, o deslocamento angular é o mesmo. Lembra como se calcula o comprimento de um arco de círculo?
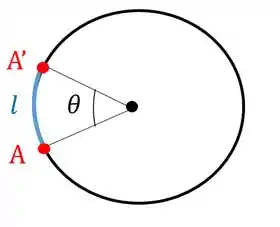
Agora vamos aplicar esta relação na nossa polia:
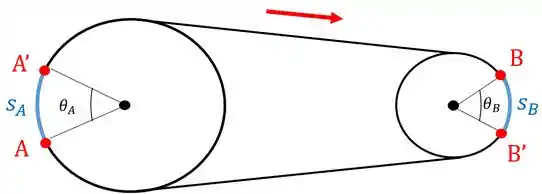
Vamos ter que o deslocamento do ponto é:
Para o ponto :
Mas como vimos, o quanto o ponto andou para chegar até é o igual ao valor do deslocamento do ponto até chegar em , então:
Seguindo este mesmo raciocínio, a corda tem a mesma velocidade quando passa pela polia e pela polia :
A componente tangencial da aceleração também não muda na corda esteja ela passando pela polia ou pela polia:
Então é só isso tudo! ![]()
Vamos fazer uns exercícios para fixarmos todas essas informações. Você verá que rapidinho pega o jeito!!!
Aceleração Angular Constante
Movimento de um Ponto pertencente ao Corpo
Transmissão de Movimento
Exercícios Resolvidos
Exercício Resolvido #1
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 251-16.3
A velocidade angular do disco é definida por , onde é dado em segundos. Determine os módulos da a) velocidade e b) aceleração do ponto do disco quando .
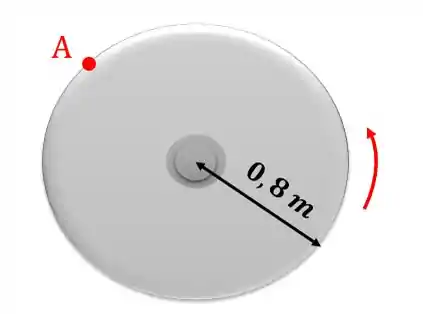
Passo 1
Para determinar a velocidade do ponto que pertence ao disco que está girando, usamos a seguinte fórmula:
Repare que para achar temos que determinar o valor de antes usando a equação que foi dado no enunciado:
Para o tempo :
Sabendo pela figura que o raio , agora sim podemos achar a velocidade do ponto A:
Passo 2
Nosso próximo passo é determinar a aceleração. Não podemos esquecer que a aceleração tem duas componentes, uma tangencial e outra normal:
Vamos achar a componente tangencial primeiro. Para isso, temos que determinar a aceleração angular :
Como , então:
Para o tempo , vamos ter o seguinte valor de aceleração:
Agora é só acharmos a aceleração tangencial:
Passo 3
Agora vamos achar a aceleração normal que é:
Nós já sabemos o valor de quando , pois já achamos isso no passo 1.
Então é só substituir:
Beleza! Como a questão pediu o módulo da aceleração é só aplicarmos o teorema de Pitágoras para achar a aceleração resultante:
Resposta
Exercício Resolvido #2
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 246-5/6
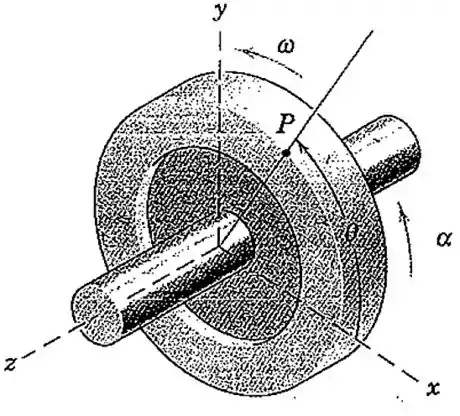
O volante possui um diâmetro de e gira com uma velocidade cada vez maior em torno de sua árvore no eixo . Quando o ponto sobre a borda cruza o eixo com , possui uma aceleração dada por . Para esse instante, determine a velocidade angular e a aceleração angular do volante.
Passo 1
Primeiro vamos entender o que está acontecendo. O volante está girando com uma velocidade que está crescendo, logo ele tem uma aceleração com duas componentes. Quando o ponto tem um ângulo de , ele possui essa aceleração aqui:
Que pode ser escrita nas suas componentes e :
Então, vamos ter os seguintes vetores:
Passo 2
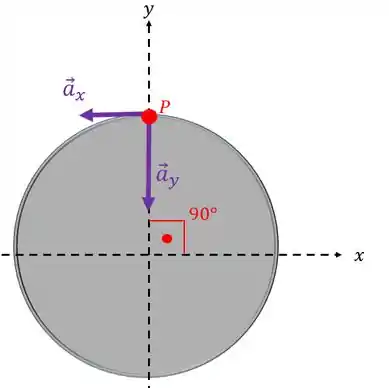
Agora vamos achar a velocidade angular do volante. Para isso, vamos usar a componente centrípeta da aceleração ().
A aceleração centrípeta sempre aponta para o centro da curva, então ela será equivalente ao nosso vetor .
Lembra como se calcula a aceleração centrípeta?
Opa, olha quem apareceu aí. É justamente a velocidade angular que queremos saber. Já sabemos que e . Agora é só alegria:
Então:
E o sentido da velocidade angular? É só usar a regra da mão direita:
Passo 3
Repare que a velocidade varia no tempo, portanto a aceleração tem componente tangencial que é responsável pela mudança do módulo da velocidade. A componente tangencial é aquele vetor que tangencia a curva, certo? Então vamos ter:
E como se calcula a aceleração tangencial mesmo? É assim né:
O raio nós sabemos que é e a aceleração tangencial nós também conhecemos que é . Então, podemos achar a aceleração angular do volante:
Não usei o sinal, porque estamos calculando o módulo. E quanto ao sentido da aceleração angular? Ela terá o mesmo sentido do vetor velocidade angular , porque está aumentando. Ou seja, aponta no sentido positivo do eixo .
Resposta
Exercício Resolvido #3
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 246-5/10
A placa forma um triângulo equilátero que gira no sentido anti-horário com velocidade crescente em torno do ponto . Se as componentes normal e tangencial da aceleração do centróide em um determinado instante são e , respectivamente, determine os valores de e nesse mesmo instante. O ângulo é o ângulo entre a linha e o eixo horizontal fixo.
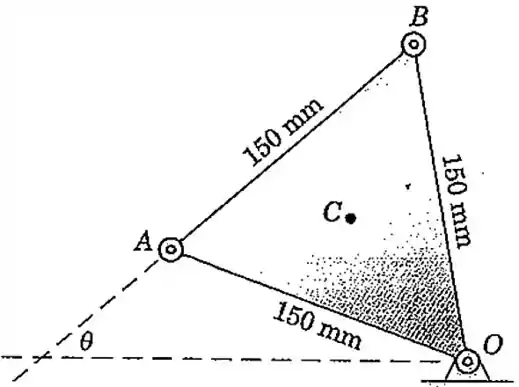
Passo 1
Primeiro vamos posicionar as coordenadas normal e tangencial () no centróide da peça:
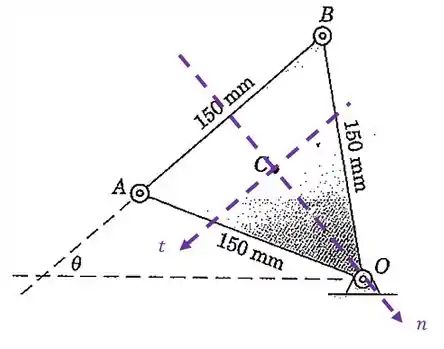
Não esqueça que o eixo aponta no sentido do movimento (anti-horário) e o eixo aponta para o centro da curva que o movimento faz. Ou seja, como o corpo gira em torno do ponto , o eixo aponta para este ponto.
Vamos colocar agora os vetores aceleração que foi dado no enunciado:
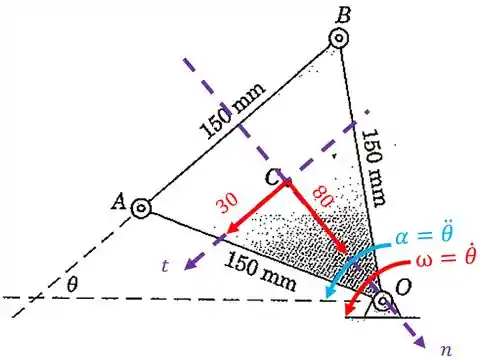
Lembra que a velocidade angular também pode ser chamada de e a aceleração angular também pode ser representada por . É justamente isso que o enunciado faz! ![]()
A aceleração tem duas componentes: uma tangencial à trajetória (aceleração tangencial) e outra normal à trajetória circular (aceleração centrípeta):
Lembra a fórmula da aceleração centrípeta?
Vamos usar esta fórmula para achar a velocidade angular do centróide. Mas para isso temos que achar o raio da trajetória circular que o centróide faz. Vamos ter o seguinte círculo:
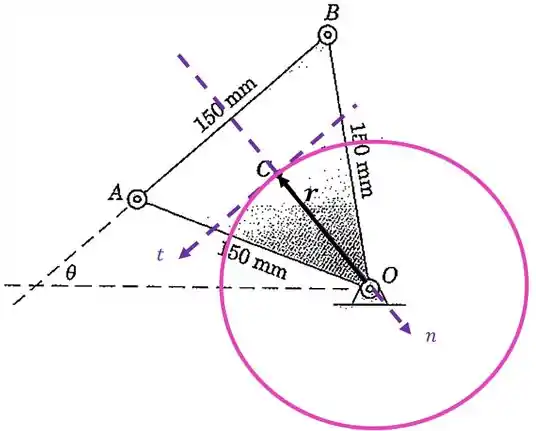
Passo 2
Vamos ter que lembrar de como é um triângulo equilátero para calcular o raio :
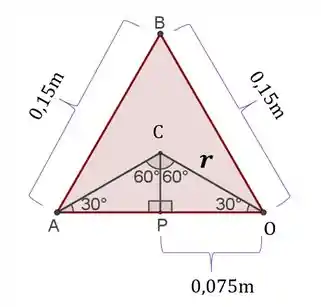
Para calcular o raio vamos usar o seguinte triângulo:
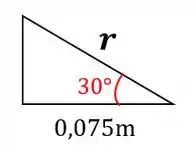
Agora podemos calcular a velocidade angular do ponto :
Podemos escrever também:
Passo 3
Nosso próximo passo é calcular a aceleração angular do ponto . Para isso, vamos usar a equação da aceleração tangencial:
Sabemos que e , então:
Resposta
Exercício Resolvido #4
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 254-16.18
Partindo do repouso quando , a polia tem aceleração , onde é dado em radianos. Determine a velocidade do bloco quando ele atinge a posiç��o . A polia tem um cubo interno que está fixo em e gira com ela.
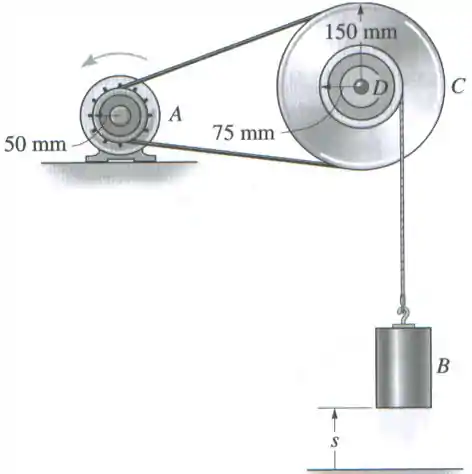
Passo 1
Quando temos duas polias ligadas por uma corda, nós vimos que o tanto que a corda andar na polia é o mesmo tanto que ela vai andar na polia . Ou seja, o deslocamento da corda tanto na polia quanto na polia deve ser o mesmo:
Repare que o bloco está ligado a polia por uma corda, então quando a polia começar a girar vai levantar o bloco . E seguindo o mesmo raciocínio de antes, conforme a polia girar ela vai enrolar a corda em torno de si. Vamos fazer um esqueminha para entendermos melhor.
Na situação inicial, quando , temos:
Quando as polias começarem a girar vamos ter:
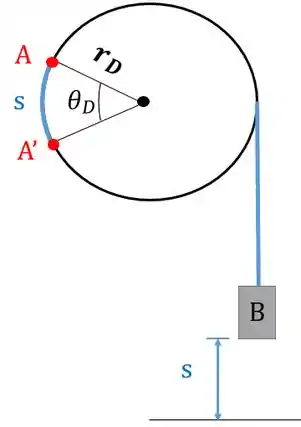
Escrevendo isso matematicamente, temos:
Mas repare que a polia D está fixa na polia C e gira com ela, de modo que:
Vamos substituir isso na equação de
Agora, vamos isolar o nas duas equações que temos até agora que são:
E:
Isolando , vamos ter:
E:
Igualando essas equações, teremos:
Vamos isolar , porque no enunciado foi dada a aceleração da polia :
Passo 2
Vamos pensar em outra relação entre as duas polias. Lembre que a velocidade da corda é sempre a mesma esteja ela passando pela polia ou pela polia , então:
Mas o que queremos saber é a velocidade do bloco B, não é mesmo?
Para calcular a velocidade angular , usamos a seguinte equação:
Mas lembra que a polia e a polia estão girando juntas? Desse modo que . Então, essas duas polias têm a mesma variação do ângulo em relação ao tempo, portanto vão ter a mesma velocidade angular:
Podemos dizer, então que:
Agora, vamos substituir na seguinte equação:
Passo 3
Até agora temos duas equações:
E:
Temos que arranjar um jeito dessas duas equações virar uma só. Vamos achar as variáveis que se repetem nas duas equações: e . Vamos isolar essas variáveis em ambas as equações:
E:
Vamos igualar as equações e isolar o que queremos saber que é o :
Simplificando, temos:
Passo 4
Agora temos que dar um jeito de achar uma relação entre a velocidade angular e a deslocamento angular da polia . Qual é a equação que relaciona essas duas variáveis?
Opa, vamos ter que integrar o lado esquerdo com relação a e o lado direito com relação a :
Lembrando que o enunciado disse que . Vamos colocar isso na nossa integral:
Sabemos que o sistema partiu do repouso então e . Vamos ter que:
Vamos substituir nesta equação aqui:
Simplificando vamos ter:
Então, quando s = 6 m, a velocidade do bloco B será:
Resposta
Exercício Resolvido #5
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 254-16.22
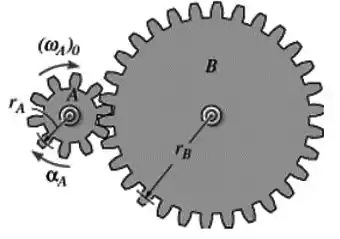
Um motor gira uma engranagem com aceleração , onde é dado em radianos. Se tem velocidade angular inicial , determine a velocidade angular da engrenagem após ter sofrido um deslocamento angular de .
Dados: e .
Passo 1
Nós temos uma aceleração da engrenagem que varia com o deslocamento angular e temos a velocidade angular inicial desta mesma engrenagem. Que equação relaciona essas duas grandezas?
Vamos ter que integrar de ambos os lados, sabendo que :
Qual será o nosso intervalo de integração? Sabemos que o deslocamento angular da engrenagem é de . Para converter revolução para radianos, temos que saber que:
Então, terá:
Já temos um intervalo de integração:
E para a velocidade angular, temos a informação que a velocidade angular inicial da engrenagem é de . Já a sua velocidade angular final é o que queremos saber, pois é através dela que iremos calcular a velocidade da outra engrenagem.
Agora é só integrar:
Substituindo os valores teremos:
Passo 2
Agora temos que lembrar da relação que temos entre a transmissão de movimento entre duas polias ou engrenagens:
Então, a velocidade angular da engrenagem será:
Temos que e , então:
Resposta
Exercício Resolvido #6
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 255-16.30
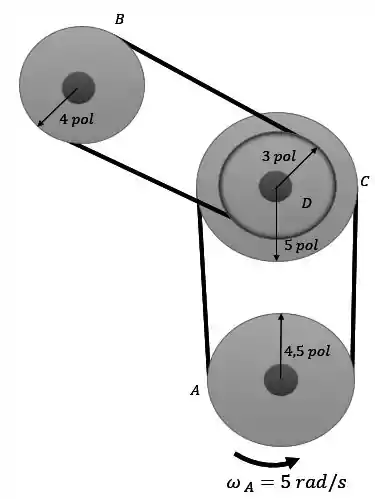
Um moinho usa um arranjo de polias e correias para transmissão de potência. Quando , um motor elétrico está girando a polia com velocidade angular . Se a polia está sujeita a uma aceleração angular de , determine a velocidade angular da polia após esta ter executado 6 revoluções. O cubo em está rigidamente conectado à polia , girando com ela.
Passo 1
Nesse exercício temos que trabalhar com as fómulas de transmissão de movimento entre as polias, tanto de velocidade angular:
Quanto de aceleração angular:
A polia possui uma velocidade angular inicial de , então vamos ir transmitindo isso para as outras polias até acharmos a velocidade angular inicial da polia .
Repare que a polia está conectada à polia , então:
Observe que a polia está conectado com a polia , girando com ela. Então, a polia realiza os mesmos movimentos que a polia :
Agora repare que a polia está conectada pela corda com a polia , então vamos ter que:
Opa, já temos a velocidade da polia quando !
Passo 2
Nosso próximo passo é trabalhar com a aceleração. Como a polia foi submetida a uma aceleração angular constante, quando ela for transmitindo seu movimento, cada polia terá sua própria velocidade angular constante.
A polia está conectada com a polia , então vamos ter que:
Como vimos antes, a polia está conectada rigidamente à polia , logo todo movimento que faz, a polia também vai fazer. Então:
Como a polia está ligada à polia , a sua aceleração será:
Essa é a aceleração angular da polia e ela é constante assim como a aceleração angular da polia também é constante.
Passo 3
Agora temos que calcular a velocidade angular final da polia após ela ter dado 6 revoluções.
Para isso temos que saber que:
Então, para 6 revoluções teremos:
Esse é o deslocamento angular da polia .
Como a aceleração angular é constante, temos que procurar uma equação que relacione velocidade angular e deslocamento angular:
O deslocamento inicial ()da polia é zero, então:
Resposta
Exercício Resolvido #7
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 248-5/25
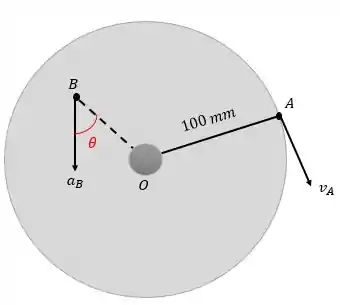
O disco circular gira em torno de seu centro . Em um determinado instante o ponto possui uma velocidade na direção mostrada, e no mesmo instante a tangente do ângulo dado pelo vetor aceleração total de um ponto qualquer com sua linha radial até é de 0,6. Calcule para esse instante a aceleração angular do disco.
Passo 1
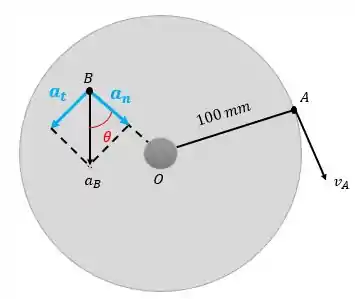
A aceleração de um ponto que pertence a um corpo rígido que esteja realizando rotação, pode possuir duas componentes: uma tangencial e outra centrípeta.
A componente tangencial é tangente à trajetória e aponta na direção do movimento do disco:
E a componente normal é perpendicular à trajetória aponta para o centro do disco:
Passo 2
Precisamos achar a velocidade angular do disco. Para isso, vamos usar a informação sobre o ponto .
O ponto tem um velocidade e sabemos que a velocidade de um ponto que pertence a um corpo rígido em rotação é:
Então:
Repare que a velocidade angular é negativa, pois faz o disco girar no sentido horário.
Então, já podemos calcular a componente normal da aceleração do ponto:
Por enquanto vamos deixar em função do raio, pois não sabemos seu valor.
Passo 3
Agora vamos calcular a aceleração angular. Para isso, temos que usar a informação de que a tangente do ângulo dado pelo vetor aceleração total de um ponto qualquer com sua linha radial até é de 0,6:
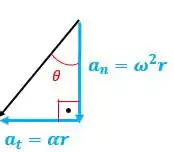
Como já sabemos que , então: