Exercícios de Rotação de Corpos Rígidos - Lista de Exercícios Resolvida
Questão 1
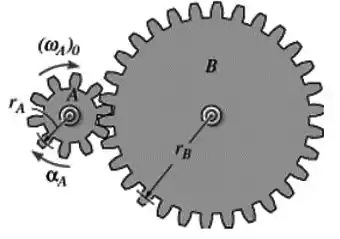
Um motor gira uma engranagem com aceleração , onde é dado em radianos. Se tem velocidade angular inicial , determine a velocidade angular da engrenagem após ter sofrido um deslocamento angular de .
Dados: e .
Questão 2
A velocidade angular do disco é definida por , onde é dado em segundos. Determine os módulos da a) velocidade e b) aceleração do ponto do disco quando .
Questão 3
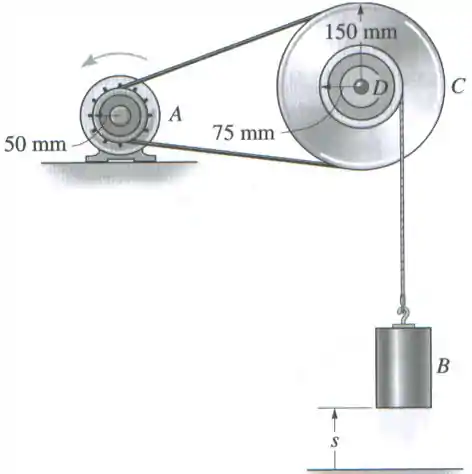
Um moinho usa um arranjo de polias e correias para transmissão de potência. Quando , um motor elétrico está girando a polia com velocidade angular . Se a polia está sujeita a uma aceleração angular de , determine a velocidade angular da polia após esta ter executado 6 revoluções. O cubo em está rigidamente conectado à polia , girando com ela.
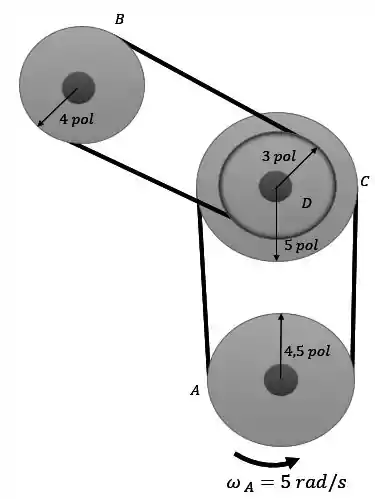
Questão 4
A placa forma um triângulo equilátero que gira no sentido anti-horário com velocidade crescente em torno do ponto . Se as componentes normal e tangencial da aceleração do centróide em um determinado instante são e , respectivamente, determine os valores de e nesse mesmo instante. O ângulo é o ângulo entre a linha e o eixo horizontal fixo.
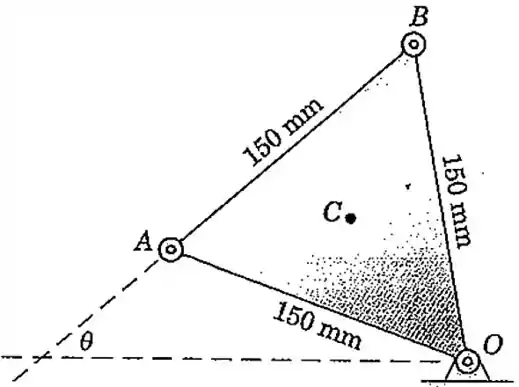
Questão 5
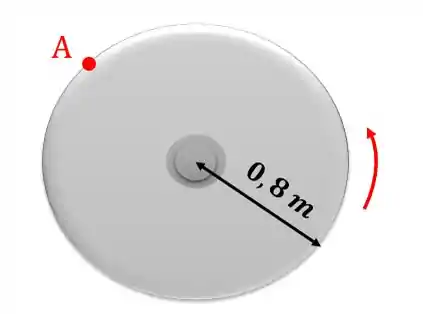
O disco circular gira em torno de seu centro . Em um determinado instante o ponto possui uma velocidade na direção mostrada, e no mesmo instante a tangente do ângulo dado pelo vetor aceleração total de um ponto qualquer com sua linha radial até é de 0,6. Calcule para esse instante a aceleração angular do disco.
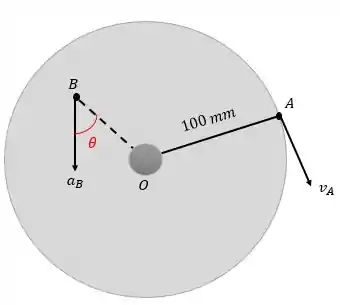
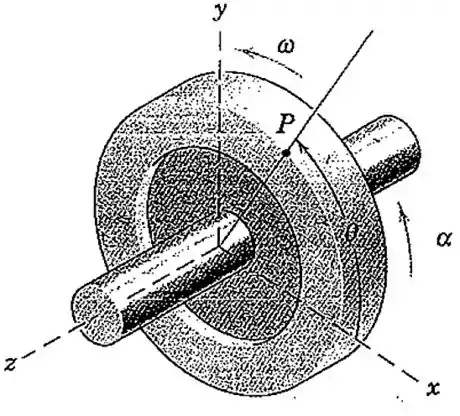
Questão 6
O volante possui um diâmetro de e gira com uma velocidade cada vez maior em torno de sua árvore no eixo . Quando o ponto sobre a borda cruza o eixo com , possui uma aceleração dada por . Para esse instante, determine a velocidade angular e a aceleração angular do volante.