Cálculo das deformações devido a temperatura e recalque
Produzido por Pablo RicardoTeoria
Introdução
Como vimos na aula de deformação devido a carregamento externo, vimos que sempre teremos duas estruturas:
- Primeiro a estrutura hiperestática
- Segundo a estrutura isostática proveniente da estrutura hiperestática.
E depois vimos que podemos escolher duas situações para determinar as deformações:
- Caso 1 – carregamento externo na estrutura hiperestática, e carregamento unitário na isostática
- Caso 2 – carregamento externo na estrutura isostática, e carregamento unitário na estrutura hiperestática.
Agora com relação a temperatura e recalque, teremos o mesmo funcionamento, mas veremos que existe uma maneira simples e uma maneira complexa de escolher os sistemas a serem analisados.
Caso 1 (temperatura) – Carregamento de temperatura no sistema isostático e carregamento unitário no sistema hiperestático.
Esse caso 1, já adianto que é o mais fácil de se resolver. Porque? ora, porque tanto variação de temperatura quanto recalque do apoio, em sistemas isostáticos, produzem diagramas de momento, normal e cortante, iguais a zero, ou seja, podemos adiantar que os seguintes esforços no sistema isostático com carregamento de temperatura serão zero:
Porém o sistema hiperestático com carregamento unitário não terá diagramas iguais a zero, e seus esforços são representados como:
mas qual fórmula vamos usar? Além do mais, a combinação dos diagramas, só vale para o caso de carregamento externo, para temperatura, e especificamente para o nosso caso 1 a fórmula será dada por:
E perceba, se tirarmos das integrais os valores constantes, teremos que:
Em que:
Então por exemplo, imagine que tenhamos o seguinte exemplo novamente.

E que eu diga que a diferença de temperatura entre as fibras internas e externas seja de 20° e que a altura da viga seja de 60cm, com coeficiente de dilatação térmico de . Qual o deslocamento vertical do centro da viga?
Já sabemos que se colocarmos a variação de temperatura no sistema isostático o diagrama será zero. Também sabemos que os efeitos dos esforços normais, também são zero, com isso nossa equação se simplifica da seguinte maneira:
Aplicando a carga unitária no sistema hiperestático teremos que:
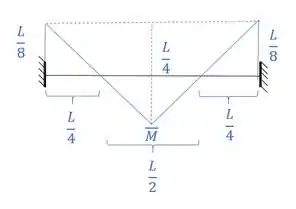
Esse é o nosso diagrama de momentos fletores, em que sabemos que a área será positiva em baixo, e negativa em cima, sendo assim a nossa área resultante será:
Se a área é zero, teremos que a nossa deformação será:
Caso 2 (temperatura) – Carregamento de temperatura no sistema hiperestático e carregamento unitário no sistema isostático
Esse caso já é mais complexo, mas irá funcionar exatamente da mesma maneira, porém com uma fórmula mais complexa, pois veja:
Se colocarmos o carregamento unitário no sistema isostático, iremos gerar diagramas de momentos fletores, normais e cortantes que serão representados da seguinte maneira:
E perceba, se colocarmos a variação de temperatura no sistema hiperestático, o diagrama não vai mais ser zero, e nesse caso irá gerar os seguintes esforços:
e com isso a nossa fórmula também irá mudar, e agora, indo pelo caos dois, se quisermos determinar a deformação, deveremos usar a seguinte equação:
perceba que o conceito permanece igual, as integrais referentes a temperatura podem ser simplificadas e podemos usar as áreas dos diagramas, enquanto que as integrais sem temperatura, podemos usar a combinação de diagramas. Mas no fim das contas, para temperatura, o caso 1 sempre será a melhor estratégia.
Caso 1 (recalque) – Carregamento de recalque no sistema isostático e carregamento unitário no sistema hiperestático.
Esse caso 1 para recalque segue o mesmo principio da temperatura, mas agora ao invés de analisar os diagramas vamos olhar as reações de apoio.
Perceba que, se colocarmos o recalque no sistema isostático, assim como a temperatura o diagrama será zero, e não precisaremos nos preocupar com as reações de apoio.
Sendo assim a nossa fórmula será:
Em que:
Sendo assim, analisamos a estrutura hiperestática com o carregamento unitário, vamos supor que queremos saber a deformação vertical do ponto central da nossa estrutura do exemplo anterior:

E sabemos que ela sofreu um recalque no apoio da direita de 2cm para baixo.
De cara se colocarmos o recalque do apoio na estrutura isostática, já sabemos que o diagrama e as reações de apoio serão zero nesse sistema, com isso analisamos o sistema isostático com a carga unitária.
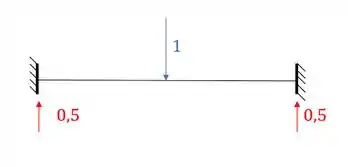
Sabemos que a deformação se dá no apoio mais a esquerda e para baixo, ou seja, como a reação é para cima e a deformação foi para baixo, temos que o valor entrará na fórmula com sinal negativo:
Sendo assim teremos:
E assim determinamos bem tranquilamente a deformação na nossa estrutura.
Caso 2 (recalque) – Carregamento de recalque no sistema hiperestático e carregamento unitário no sistema isostático.
E de novo, como na temperatura, esse caminho é mais complexo, pois nesse caso temos que tanto a carga unitária no sistema isostático, quanto a carga de recalque no sistema hiperestático produziram diagramas de esforços solicitantes, que podemos definir como:
- Esforços provenientes da estrutura hiperestática com carregamento de recalque
- Esforços provenientes da estrutura isostática com carregamento unitário
e ainda temos mais um carinha que aparece que é:
E sabendo todos os esforços a nossa fórmula será dada por:
perceba que o conceito permanece igual, o somatório fazendo referência as reações de apoio do sistema com a carga unitária, enquanto que as integrais, após o igual, podemos usar a combinação de diagramas. Mas no fim das contas, para recalque, o caso 1 sempre será a melhor estratégia.
Entendido isso tudo, bora fazer exercício pra podermos ficar mais tranquilo com essa matéria.
Vamos por a mão na massa?

Caso 2 (temperatura) – Carregamento de temperatura no sistema hiperestático e carregamento unitário no sistema isostático
Caso 1 (recalque) – Carregamento de recalque no sistema isostático e carregamento unitário no sistema hiperestático.
Caso 2 (recalque) – Carregamento de recalque no sistema hiperestático e carregamento unitário no sistema isostático.
Exercícios Resolvidos
Exercício Resolvido #1
Origem do Exercício
O pórtico abaixo sobre um recalque em A na vertical e para baixo de 2cm, e em B, sofre um deslocamento horizontal e para direita de 5cm. Sabendo disso, determine o deslocamento horizontal do ponto C.
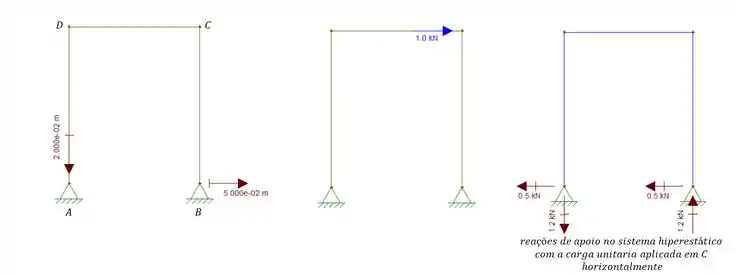
Passo 1
Se olharmos o nosso desenho vamos perceber que o diagrama de reações de apoio com a carga unitária que nos foi dado é na estrutura hiperestática. Ou seja, é como se os carregamentos de recalque fossem aplicados na estrutura isostática, que já sabemos antecipadamente que produzira um diagrama zero. E como aplicamos a carga unitária na estrutura hiperestática, no ponto e na direção que queríamos saber o recalque, vamos ter que:
Em que:
Olhando a nossa estrutura vamos ter que:
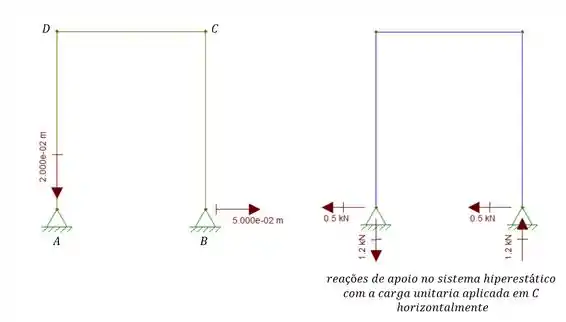
- No apoio em A temos um deslocamento de 2cm para baixo e uma reação de 1,2kN para baixo também, o que significa que como estão na mesma direção, a combinação deles vai ser positiva.
- Já no apoio B, o deslocamento é de 5cm para direita, enquanto a reação é de 0,5kN para esquerda, o que significa que a combinação deles vai ser negativa, e sendo assim vamos ter que:
Perceba que o deslocamento deu positivo, ou seja, é o mesmo ao que supomos para a carga unitária, ou seja, o ponto C desloca, 0,1cm, ou 1mm para direita.
Resposta
Exercício Resolvido #2
Origem do Exercício
Uma viga possui suas fibras superiores resfriando a -20°C e as inferiores são mantidas a 20°c. sabendo disso e usando os diagramas correspondentes abaixo, determine o deslocamento vertical do ponto B da vida dada abaixo. Supor a altura da viga como
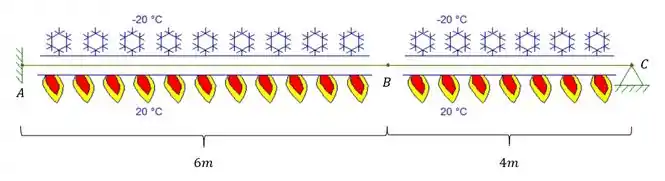
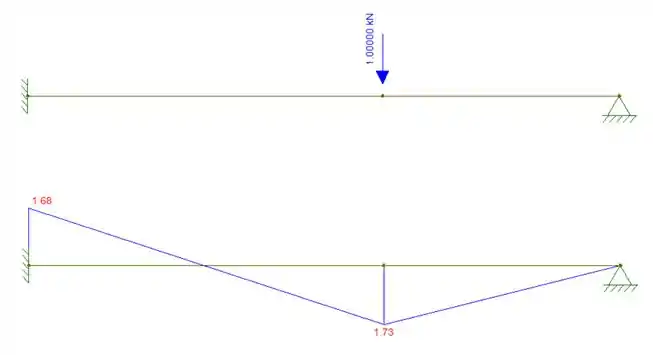
Passo 1
Perceba que aplicamos o carregamento unitário no nosso sistema hiperestático, e obtemos o diagrama de momentos fletores no sistema hiperestático devido a carga unitária.
Em contra partida, sabemos que aplicamos nosso carregamento de temperatura no sistema isostático, e que a fórmula que devemos usar é dada por:
E perceba, se tirarmos das integrais os valores constantes, teremos que:
Em que:
Porém no nosso caso de viga, pouco importa o normal, sendo assim, podemos nos concentrar basicamente nos momentos fletores, e como podemos ver, na área do diagrama de momentos fletores, e perceba, será exatamente a área do diagrama de momentos fletores devido a carga unitária no sistema hiperestático.
Sendo assim nossa fórmula será:
E podemos fazer uma regra de 3 no nosso diagrama:
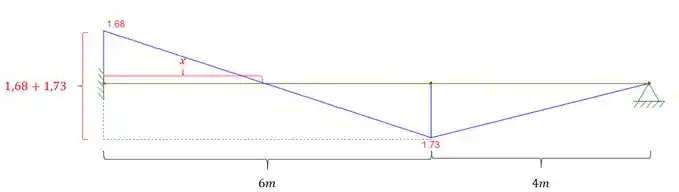
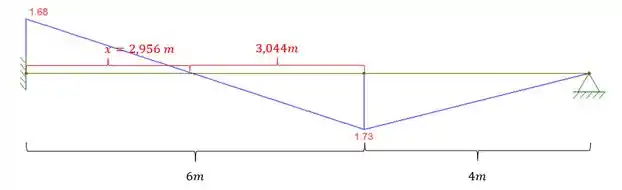
Sabemos que para determinar a área precisamos respeitar o sinal do momento, ou seja, tudo acima do eixo da viga é considerado negativo, e tudo que está abaixo é considerado positivo, e assim teremos que:
Olhando a nossa equação teremos que:
Substituindo teremos que:
Resposta
Exercício Resolvido #3
Origem do Exercício
O pórtico abaixo sobre um recalque em A na vertical e para baixo de 8cm e para esquerda de 3cm, e em E, sofre um deslocamento horizontal de 2cm para esquerda, 0.001Rad no sentido anti-horário e 12cm na vertical para cima. Sabendo disso, determine o deslocamento vertical do ponto C.
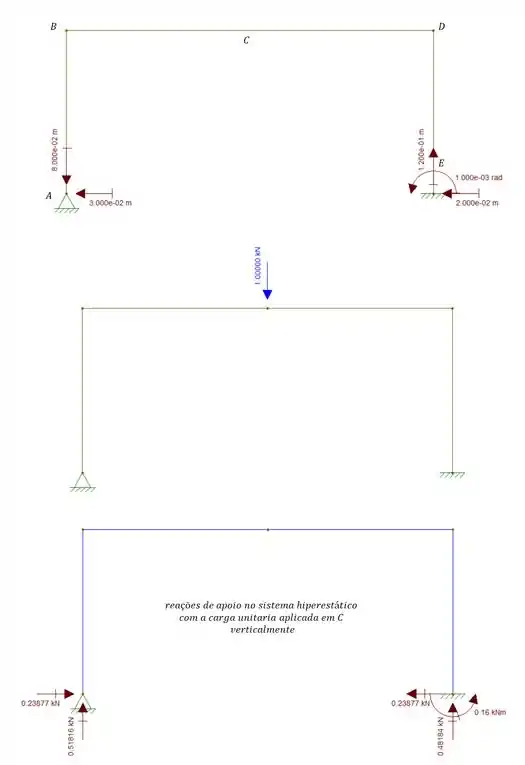
Passo 1
Se olharmos o nosso desenho vamos perceber que o diagrama de reações de apoio com a carga unitária que nos foi dado é na estrutura hiperestática. Ou seja, é como se os carregamentos de recalque fossem aplicados na estrutura isostática, que já sabemos antecipadamente que produzira um diagrama zero. E como aplicamos a carga unitária na estrutura hiperestática, no ponto e na direção que queríamos saber o recalque, vamos ter que:
Em que:
Olhando a nossa estrutura vamos ter que:

- No apoio em A temos um deslocamento de 8cm para baixo e uma reação de para cima, e como estão em direções opostas, o sinal será negativo.
- Ainda no apoio A temos um deslocamento de 3cm para esquerda e uma reação de apoio de para direita, como estão em sentidos opostos, serão novamente negativos.
- Indo para o apoio E, vemos um deslocamento de rotação de e uma reação de apoio no mesmo sentido anti-horário dado por , mas como fazemos as contas em cm, vamos mudar a unidade que vai ser . Logo essa combinação será positiva
- No apoio E também temos um deslocamento vertical de , e uma reação de apoio no mesmo sentido de . Logo essa combinação será positiva.
- E por fim no apoio E ainda temos um deslocamento de para a esquerda, com uma reação de apoio na mesma direção de . Logo essa combinação será positiva também.
Perceba que o deslocamento deu negativo, ou seja, é o oposto ao que supomos para a carga unitária, ou seja, o ponto C desloca, , para cima.
Resposta
Exercício Resolvido #4
Elaboração própria
A viga abaixo está sujeita a uma variação de temperatura de 35°C entre suas fibras superiores e inferiores. Sabendo disso e utilizando o diagrama de momento fletor para uma carga unitária vertical apontado para baixo aplicada em , determine o deslocamento vertical do ponto da viga. Supor a altura da viga e coeficiente de dilatação linear como:
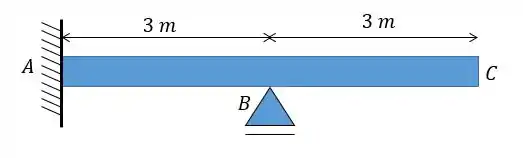
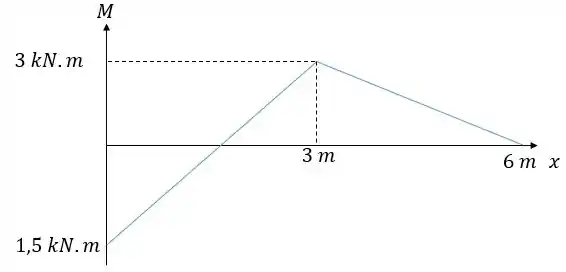
Passo 1
Fala aí, pessoal!!! Olha essa questão que interessante... Ela pede para que a gente determine o deslocamento vertical da extremidade em balanço , e o que vai causar esse deslocamento?
Exatamente, a diferença de temperatura que vai envergar a nossa viga... E para a gente calcular esse deslocamento a gente precisa utilizar aquela nossa equaçãozinha que é dada por:
E o que precisamos, além das condições de temperatura, é achar o diagrama do momento fletor e da força normal que atuam na nossa viga. Mas não tem carregamento né? E aí?
Bom, para que a gente resolva nós temos de colocar um carregamento unitário no sentido vertical exatamente no ponto onde queremos achar o deslocamento. Então vai ficar assim:
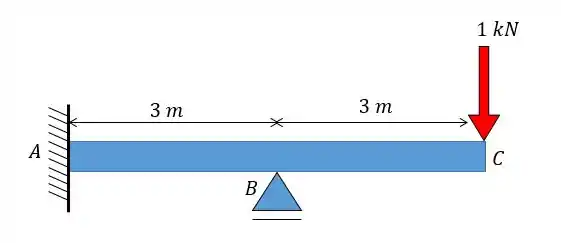
Aí a partir desse nosso carregamento unitário que vamos achar o momento fletor, normal e aplicar na nossa equação, beleza?
Passo 2
Mas galera, o problema já nos forneceu esse diagrama né? Caso você tenha ficado curioso para achar as reações vou mostrar aqui embaixo junto com o diagrama também. Perceba que o ponto principal dessa questão é aprender a utilizar a equação para temperatura e não ficar calculando reações de sistemas hiperestáticos, beleza?
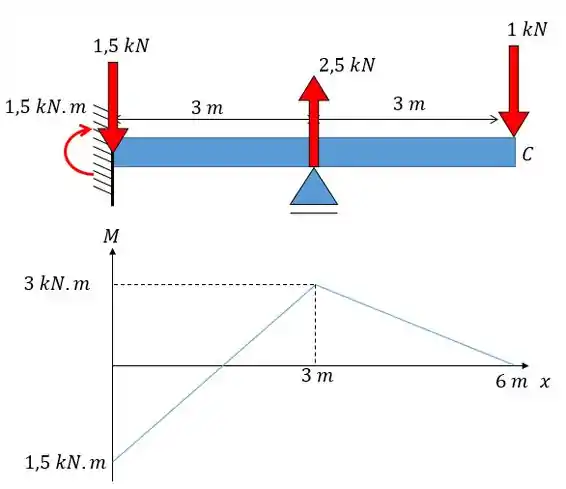
Repara como não existem forças na horizontal... Então a nossa equação, não vai precisar do termo referente à normal:
Retirando o termo da normal e colocando as constantes para fora da integral vamos ter:
Onde é o deslocamento que queremos calcular, é a força unitária, e o problema deu, assim como a variação da temperatura. Então só precisar achar a integral do momento fletor que é a própria área do diagrama de momento fletor.
Passo 3
Olhando novamente o diagrama nós temos:
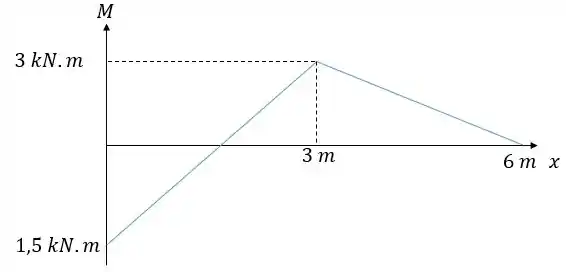
Se acharmos o pontinho de interseção ali no eixo acabou o problema. Então por semelhança vamos utilizar os lados apostos aos ângulos em preto e os lados referentes ao eixo :
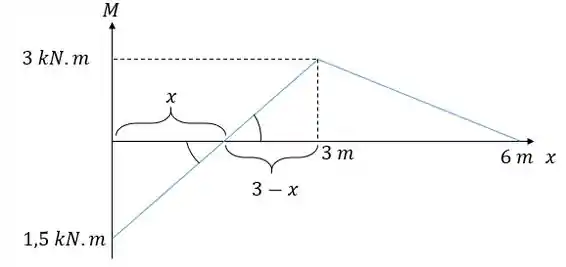
Agora a gente só precisa lembrar que o que está acima do eixo é negativo e abaixo positivo, até mesmo para a área. Então vamos ter:
Passo 4
Agora é só jogar na equação:
Por que para baixo? Porque achamos um valor positivo, ou seja, condizente com a força unitária para baixo.
Resposta
Exercício Resolvido #5
Origem do Exercício
Abaixo nos é dado um pórtico que sofre os recalques mostrados na figura. Sabendo que as reações de apoio dadas são referentes a uma carga untaria aplicada em C na direção horizontal e no sentido mostrado, determine o deslocamento horizontal do ponto C.
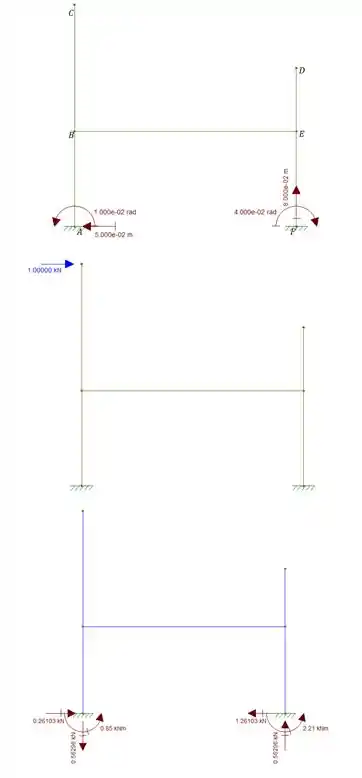
Passo 1
Se olharmos o nosso desenho vamos perceber que o diagrama de reações de apoio com a carga unitária que nos foi dado é na estrutura hiperestática. Ou seja, é como se os carregamentos de recalque fossem aplicados na estrutura isostática, que já sabemos antecipadamente que produzira um diagrama zero. E como aplicamos a carga unitária na estrutura hiperestática, no ponto e na direção que queríamos saber o recalque, vamos ter que:
Em que:
Olhando a nossa estrutura vamos ter que:
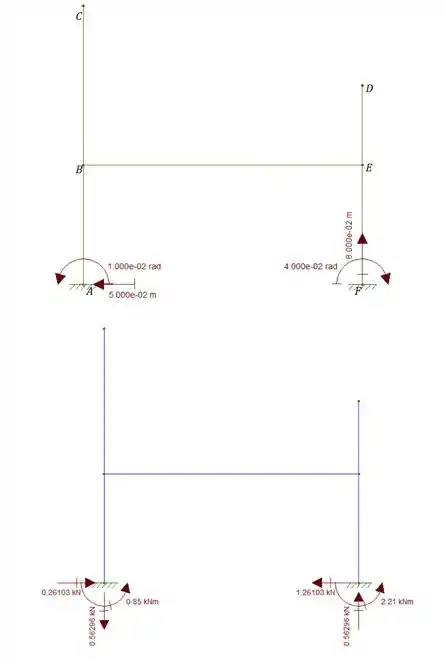
- No apoio em A temos um deslocamento de 5cm para esquerda e uma reação de para direita, e como estão em direções opostas, o sinal será negativo.
- Ainda no apoio A, vemos um deslocamento de rotação de e uma reação de apoio no mesmo sentido anti-horário dado por , mas como fazemos as contas em cm, vamos mudar a unidade que vai ser . Logo essa combinação será positiva
- No apoio F temos um deslocamento vertical de , e uma reação de apoio no mesmo sentido de . Logo essa combinação será positiva.
- E por fim no apoio F ainda temos uma rotação de no sentido horário, com uma reação de apoio no sentido oposto de . Passando para cm teremos que o nosso momento será . Logo essa combinação será negativa.
Perceba que o deslocamento deu positivo, ou seja, é no mesmo sentido ao que supomos para a carga unitária, ou seja, o ponto C desloca, , para direita.
Resposta
Exercício Resolvido #6
Elaboração própria
Dada a viga abaixo e sabendo que essa viga trabalha num local onde sua superfície superior se encontra acima da superfície inferior. Determine o deslocamento vertical do ponto mostrado. Considere a altura da viga e o coeficiente de dilatação linear como:
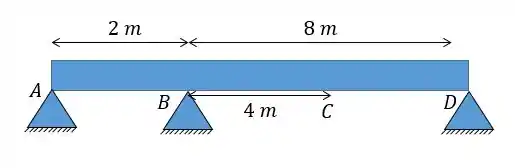
Caso necessário utilize o seguinte diagrama de momento fletor para a carga mostrada:
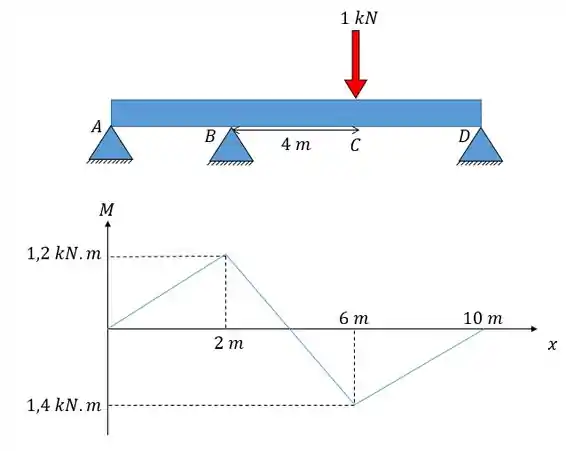
Passo 1
Vamo lá rapaziada marota, partiu resolver mais um exercício de temperatura aplicada à viga. Nesse caso o problema nos fornece uma viga sem carregamento, apenas com a variação de temperatura a qual suas fibras estão sujeitas. Dessa forma ocorrerá uma deflexão exatamente por causa da diferença de dilatação térmica entre as fibras.
Essa deflexão (ou deslocamento) pode ser calculado a partir da seguinte equação:
Então perceba que o problema nos fornece quase todos os dados: nós só temos de encontrar o momento fletor e a normal. Para encontrar esses termos a gente tem que aplicar uma carga unitária no ponto e na direção que queremos descobrir o deslocamento. No caso em questão irá ficar assim:
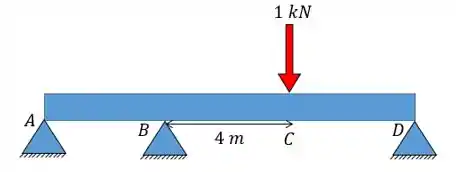
Exatamente o que o problema nos forneceu né? Que bonzinho... hahha
Repara só que o problema deu o diagrama de momento fletor e não forneceu o da normal. Por quê? Porque não tem normal oras... Então a nossa equação vai ficar como:
Lembrando que a gente quer o deslocamento vertical que é dado por , ok?
Acho que já entendemos o problema né? Partiu resolver
Passo 2
Agora vamos dar uma facilitada na nossa expressão:
Nós podemos retirar os termos que são constantes da integral e obter:
Aí todos esses termos que são constantes o problema já forneceu, só falta achar a integral do momento fletor. Mas aqui cabe ressaltar que essa integral vai ser igual à área do diagrama, que o problema também forneceu!!! Ahhh tá muito fácil isso aqui gentemmm..
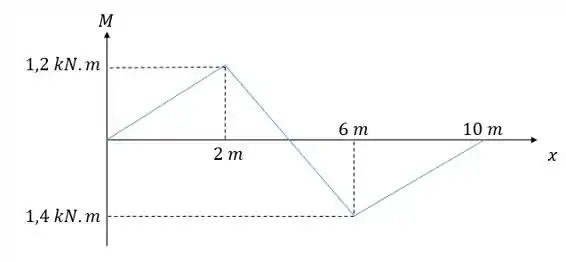
Então vamos achar essa área, para isso vamos ter que achar o ponto de interseção da curva com o eixo , podemos fazer isso por semelhança de triângulos:
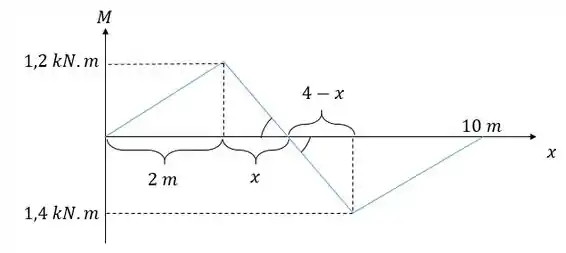
Fazendo a relação entre os lados opostos aos ângulos indicados igual à relação entre as bases vamos ter:
Passo 3
Agora podemos calcular as áreas, assim nós vamos ter:
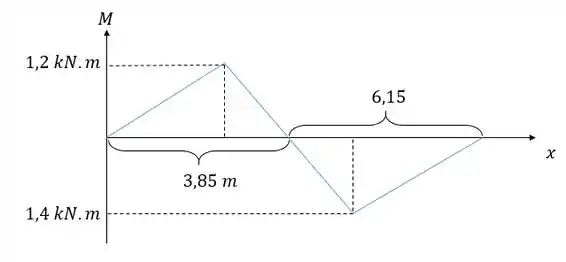
Lembrando que nesse tipo de diagrama o momento fletor negativo é representado acima do eixo , logo as áreas acima desse eixo vão ter um sinal negativo associado.
Passo 4
Agora é só substituir na equação:
Por que para baixo? Porque achamos um valor positivo, ou seja, condizente com a força unitária para baixo.
Resposta
Exercício Resolvido #7
Origem do Exercício
Determine para o ponto B da viga o seu deslocamento vertical. Saiba que na estrutura hiperestática foi usado uma carga unitária vertical em B, que apresentou as reações de apoio mostradas na figura. Assim como os deslocamentos também são mostrados na figura.
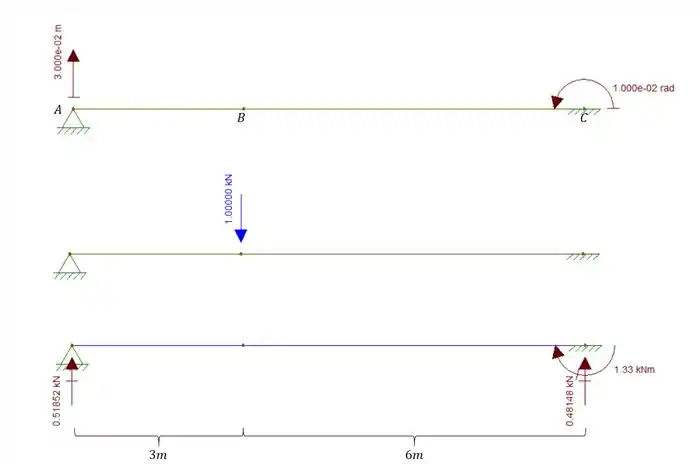
Passo 1
Se olharmos o nosso desenho vamos perceber que o diagrama de reações de apoio com a carga unitária que nos foi dado é na estrutura hiperestática. Ou seja, é como se os carregamentos de recalque fossem aplicados na estrutura isostática, que já sabemos antecipadamente que produzira um diagrama zero. E como aplicamos a carga unitária na estrutura hiperestática, no ponto e na direção que queríamos saber o recalque, vamos ter que:
Em que:
Olhando a nossa estrutura vamos ter que:

- no apoio em A temos um deslocamento de 3cm para cima, e uma reação de apoio de na mesma direção, ou seja, essa combinação será positiva.
- No apoio em B temos uma rotação de , com uma reação de momento fletor no sentido oposto dada por 1,33kNm. Como estamos fazendo os cálculos em cm, devemos converter a unidade e assim teremos que a reação será 133kNcm.
Perceba que o deslocamento deu negativo, ou seja, é no sentido contrário ao que supomos para a carga unitária, ou seja, o ponto B desloca, , para cima.
Resposta
Exercício Resolvido #8
Elaboração própria
A viga abaixo encontra-se num lugar onde suas fibras inferiores estão a uma temperatura de e as fibras superiores a uma temperatura de . Sabendo que uma força de é aplicada na sua extremidade , calcule o deslocamento dessa extremidade considerando que a distribuição de temperatura é uniforme e que a altura e o coeficiente de dilatação linear são:
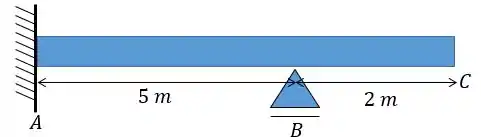
Caso necessite utilize o seguinte diagrama:
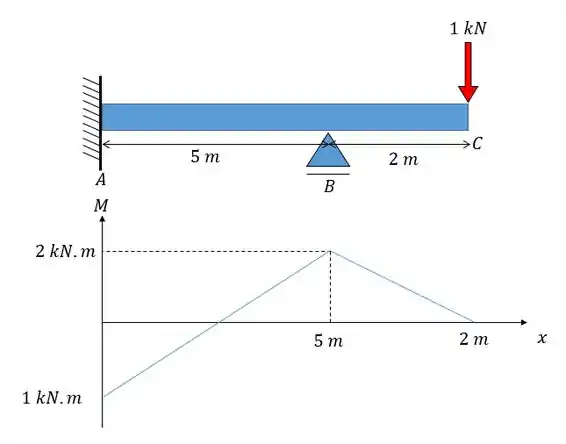
Passo 1
Galerinha, essa questão aqui fala mais um pouquinho sobre como a variação de temperatura vai influenciar na deflexão da nossa viga. O problema quer exatamente isso, a deflexão no ponto que é dada pela equação:
Como não há forças normais e também existem vários termos constantes, que podem sair da integral, vamos ter isso aqui:
Todos os termos que são constantes e foram retirados da integral o problema já nos forneceu, e a gente quer achar a deflexão, logo, . Aí é só lembrar que é a nossa força unitária apontada na direção do deslocamento que queremos encontrar (vertical) e é o diagrama de momento fletor referente à essa força , que nos foi dado!!
Então partiu resolver esse probleminha
Passo 2
Como a gente acabou de ver temos quase todos os termos, só não temos a integral. Mas essa integral é igual a área do diagrama:
Então vamos calcular a área desse diagrama:
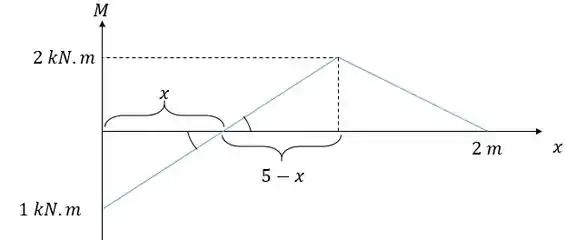
Fazendo semelhança de triângulos nós vamos ter:
Aí a gente só tem que lembrar que as áreas acima do eixo são negativas porque representam momentos fletores negativos, sendo assim:
Passo 3
Agora é só substituir na equação!!
Lembre-se que está apontado para baixo porque condiz com o sentido da força unitária.