Cargas Excêntricas e Flexão Assimétrica
Produzido por Pablo RicardoTeoria
![]()
Atenção: Esse assunto não é cobrado por muitos professores.
Agora, se você já tiver visto em sala algum exercício em que momentos foram aplicados em mais de uma direção, ou se você já viu a fórmula...
...ou alguma outra fórmula parecida, então vale a pena estudar esse tópico. 😉
Introdução
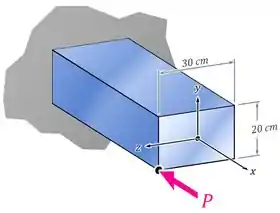
Vamos dizer que você tem a viga da imagem abaixo e aplica uma força de compressão bem no canto dela:
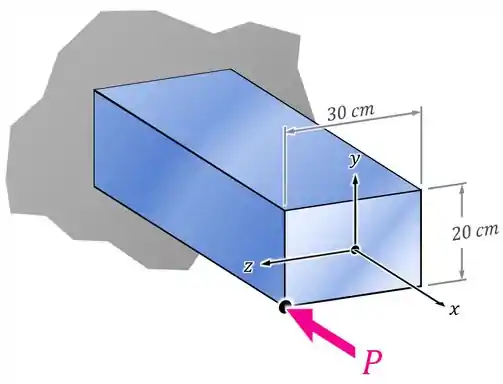
Essa força é excêntrica: ela está atuando fora do centro da seção transversal da viga.
Por ser uma força de compressão, ela vai gerar uma força interna normal na viga.
Mas por ser excêntrica, ela também vai gerar, além dessa força normal, momentos na viga:
- Por estar à esquerda do eixo vertical , ela vai gerar um momento fletor (ou “”) em relação a esse eixo , flexionando a viga para a esquerda;
- E por estar abaixo do eixo horizontal , ela vai gerar um momento fletor (ou “”) em relação a esse eixo , flexionando a viga para baixo.
Como mostra a imagem abaixo:
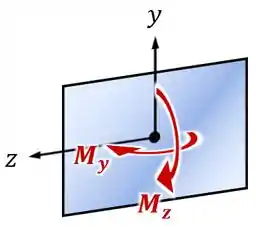
Perceba que a carga é excêntrica, mas os momentos e atuam sobre o eixo de simetria!
Lembrete de tensão normal
Para calcular as tensões normais , num ponto , em uma peça devido a um momento fletor aplicado em volta do eixo horizontal , utiliza-se a fórmula da flexão:
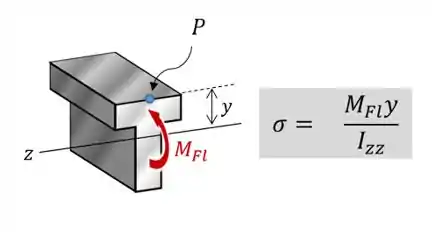
Onde:
- é o momento atuante no eixo .
- é a distância entre o eixo e o ponto .
- é o momento de inércia da seção com relação ao eixo .
Tensão normal para o caso assimétrico
Mas agora, nós temos um caso de flexão assimétrica, em que existem momentos em duas direções, sendo que esses dois momentos vão gerar tensões normais na peça.
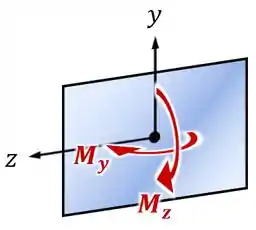
(A “assimetria” vem do fato de que se juntarmos os momentos e , o momento fletor resultante não vai estar em volta de um eixo de simetria.)
Além disso, ainda temos um força normal nessa viga, que também vai gerar tensões normais nela, de acordo com a fórmula (o sinal negativo existe porque estamos falando de uma compressão).
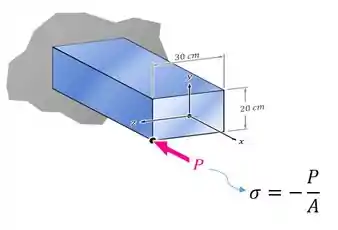
Então nesse caso, como devemos calcular as tensões normais na peça??
Nós vamos somar esses três termos relativos: à força compressiva e aos dois momentos fletores e . Mas para isso vamos precisar da regrinha da mão direita.
Regra da Mão Direita
O primeiro passo para calcular as tensões normais na peça vai ser definir bem os esforços internos nela (, e ).
Quanto à força normal ... lembra aí!
Nós podemos definir ela como caso seja uma força de tração ou caso seja uma força de compressão.
Agora...
Quanto aos momentos e , nós sabemos que eles são calculados multiplicando a força pelos seus braços em relação aos eixos e , respectivamente.
Mas para saber se esses momentos tem valores positivos () ou negativos (), nós temos que recorrer à regra da mão direita:

Usando essa regra, é possível trocar as setas curvas que representam os momentos por setas duplas.
Caso essas setas duplas estejam no mesmo sentido dos eixos e , então elas são positivas (). Caso elas estejam no sentido contrário, elas são negativas ().
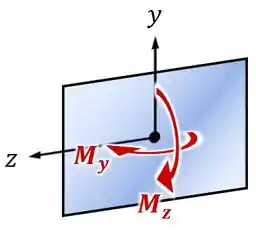
Por exemplo: fazendo essa troca para os momentos gerados pela nossa força excêntrica, vemos que os dois momentos, e , vão ter valores negativos naquele caso:
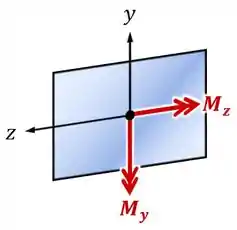
Método da Superposição
Depois que os esforços internos , e estiverem bem definidos, o segredo para resolver esses exercícios de cargas excêntricas ou flexão assimétrica está em usar o método da superposição.
Ou seja, devemos determinar o efeito de cada esforço na peça, e depois somar esses efeitos.
Quanto à força normal , sabemos que ela vai gerar uma tensão:
E quanto ao momento fletor em relação à horizontal, já sabemos que vale para ele a fórmula da flexão, que fica assim:
E como ficaria então a tensão normal no ponto do nosso exemplo por causa do momento em ?
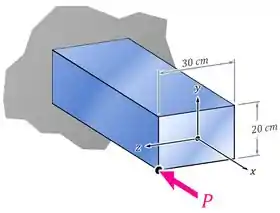
Primeiro temos de achar o momento em , que é dado pela força vezes a distância em :
Como , vamos ter:
Negativo porque já víamos que esse momento é negativo.
Agora vamos calcular o momento de inércia em relação ao eixo , assim, vamos ter:

Como estamos no eixo a nossa base vale e a nossa altura . Sendo assim:
Substituindo na equação nós vamos ter:
Como estamos calculando o valor da tensão normal exatamente no ponto e aplicação, então:
Perceba que temos um sinal positivo, logo temos uma tensão normal trativa nesse ponto.
Mas ainda falta a gente saber como é a tensão gerada por .
Então vamos pensar...
Dá para imaginar que a fórmula que descreve a tensão gerada por é semelhante à que descreve a tensão gerada por , mas com algumas diferenças.
Primeiro, a flexão causada por é em volta da vertical , então:
- A posição da fórmula da flexão tradicional relativa à linha neutra horizontal em deve ser trocada por uma posição relativa à linha neutra vertical em ;
- E o momento de inércia da área em relação ao eixo deve ser trocado por um em relação ao eixo , .
Sendo que, para o cálculo de , valem as dicas abaixo:

Concluímos que a tensão gerada por vai ser descrita pela fórmula:
Então vamos fazer esse cálculo para o nosso exemplinho:
Primeiro vamos calcular o momento , lembrando que temos de utilizar a distância em :
Como :
Lembre-se que temos um momento negativo, por causa da regra da mão direita.
Agora vamos calcular o momento de inércia em torno do eixo , lembrando agora que a base é a medida de e a altura a medida de .
Agora é só substituir:
Lembrando que o ponto está localizado em:
Então no ponto vamos ter uma tensão compressiva devido ao momento .
Para entender um pouco melhor vamos olhar o exemplo abaixo:
Para um momento positivo (), ocorre tração () para valores positivos () de e compressão () para valores negativos () de , como mostra a imagem abaixo:
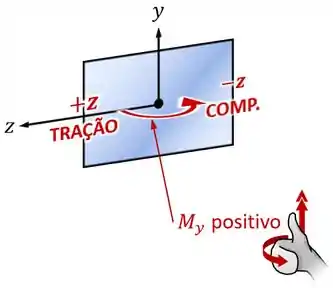
Mas no nosso exemplo é negativo certo? Então num ponto em que temos positivo vamos ter compressão ao invés de tração.
Fórmula Geral da Tensão Normal
Aí, fazendo a superposição dos efeitos de (), de () e de (), encontramos que a tensão normal em uma peça em um caso geral vai ser descrita por:
Essa fórmula pode ser usada no exemplo do início dessa teoria, ou para qualquer outro exercício de cargas excêntricas ou flexão assimétrica.
Galera, percebam que eu coloquei tudo em módulo porque não é necessário ficar decorando os sinais. A gente já calculou os valores e vimos se é compressão ou tração. Pra resolver é só colcoar um valor negativo na compressão e positivo na tração.
Então para o nosso exemplo vamos ter:
Então basta achar o valor da normal sobre a área, como a normal é igual a própria força vamos ter
Então resolvemos nosso exercício inicial, mas aqui vale ressaltar uma parada! Por acaso as duas tensões relativas aos momentos se anularam, isso nem sempre vai acontecer ok?
Então vamos partir para os exercícios e praticar um pouco mais!
Tensão normal para o caso assimétrico
Regra da Mão Direita
Método da Superposição
Fórmula Geral da Tensão Normal
Exercícios Resolvidos
Exercício Resolvido #1
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 300-4.126.
O momento é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo com a vertical. Determine a tensão no ponto , ponto e ponto .
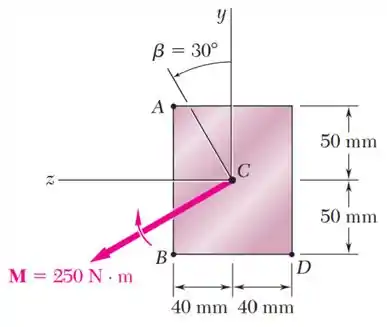
Passo 1
O que está acontecendo?
O momento pode ser decomposto em uma componente horizontal e uma componente vertical de acordo com o ângulo de indicado pelo exercício, como mostra a imagem abaixo:
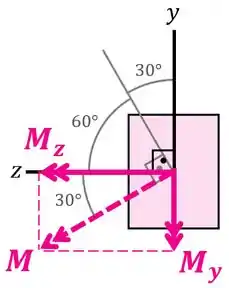
Daí que, calculando essas componentes, vamos poder descrever as tensões nessa seção transversal através da fórmula:
Sendo que nesse caso, como não temos uma força interna normal (temos só os momentos e ), essa fórmula fica assim:
E o que é que o exercício quer?
Ele quer que a gente determine as tensões :
No ponto , de posição e ;
No ponto , de posição e ;
& No ponto , de posição e .
Então, para resolver o exercício, temos que:
1. Calcular as componentes e do momento aplicado.
2. Calcular os momentos de inércia da área em relação ao eixo , , e em relação ao eixo , .
& 3. Aplicar a fórmula para os pontos , e .
Passo 2
Então primeiro, vamos calcular as componentes de .
Observando a imagem abaixo:
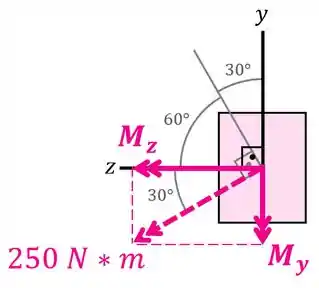
...conseguimos ver que:
E que:
Passo 3
Agora, para calcular os momentos de inércia da área e , observamos as dimensões da seção transversal:
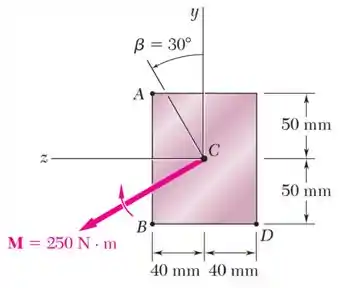
Da imagem, temos que a seção tem dimensões de .
Aqui, a fórmula do momento de inércia da área de um retângulo vale tanto para quanto para .
Além disso, nessa fórmula, a base e a altura correspondem, respectivamente, à dimensão paralela e à dimensão perpendicular ao eixo em relação ao qual se está calculando o momento de inércia da área.
Dessa forma, o momento de inércia da área em relação ao eixo vai ser:
Enquanto que o momento de inércia da área em relação ao eixo vai ser:
Passo 4
Por fim, podemos calcular a tensão em cada ponto:
Substituindo, nessas equações:
- ;
- ;
- ;
- ;
- E as posições de , e apontadas lá no passo , todas em ,
Vamos ter que:
Finalmente, calculando tudo para cada uma dessas tensões e sabendo que é o mesmo que , encontramos as nossas respostas:
Resposta
Exercício Resolvido #2
Elaboração Própria
Uma força é aplicada na plataforma da figura abaixo, que é sustentada por uma coluna retangular (em azul na figura) com uma seção transversal de . A posição da força em relação ao centro da plataforma e da coluna está indicada na figura.
Determine a tensão normal máxima nessa coluna.
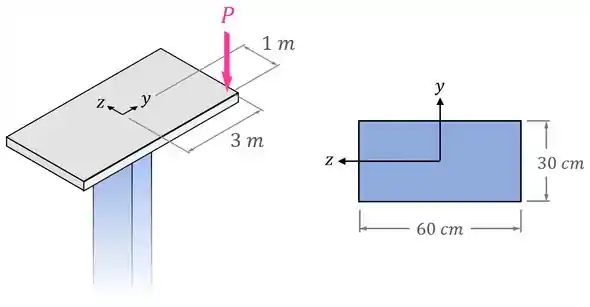
Passo 1
O que está acontecendo?
A carga excêntrica vai gerar, no centro da coluna:
- Um momento em relação ao eixo ;
- Um momento em relação ao eixo ;
- E uma força axial ,
Como mostra a figura abaixo:

Todos esses três carregamentos vão gerar tensões normais nessa coluna:
Primeiro, o momento em relação ao eixo vai gerar uma tensão normal de flexão de acordo com a fórmula da flexão de sempre:
Onde:
- é o momento em relação ao eixo , positivo no sentido que está desenhado na figura acima, que já é também o sentido do momento gerado pela força ;
- é a posição do ponto em que se quer avaliar a tensão em relação à linha neutra, localizada no eixo ;
- & é o momento de inércia da área da seção transversal dessa coluna em relação ao eixo .
Lembrando que pode ser calculado para um retângulo usando a fórmula:
Sendo que nesse caso, a base (que é paralela à linha neutra no eixo ) vai ser e a altura (perpendicular à linha neutra no eixo ) vai ser .
Segundo, o momento em relação ao eixo também vai gerar uma tensão normal de flexão .
Pela regra da mão direita, conseguimos ver que esse momento é positivo (por estar no sentido do eixo ):
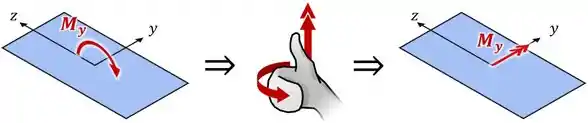
E pelo desenho dele, vemos que ele gera compressão na parte direita da coluna (com posição em relação ao eixo negativa) e tração na esquerda (com posição em relação ao eixo positiva):
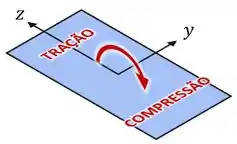
Então, para descrever a tensão devido ao momento , queremos uma fórmula:
- Semelhante à fórmula da flexão que conhecemos ;
- Mas que seja relativa ao momento , à posição em relação à linha neutra no eixo e ao momento de inércia da área em relação ao eixo , ;
- E que, para valores positivos de , resulte em valores de positivos (de tração) para valores positivos da posição e valores de negativos (de compressão) para valores negativos da posição .
Dessa forma, a nossa fórmula da flexão para o momento fica assim:
Sendo que pode ser calculado pela fórmula , mas dessa vez com uma base (paralela à linha neutra no eixo ) e uma altura (perpendicular à linha neutra no eixo ) .
Por último, nós temos que a força axial de compressão vai gerar na coluna uma força normal interna .
Sendo que a tensão gerada por essa força normal pode ser descrita pela fórmula:
Onde é a área da seção transversal da coluna.
O que tudo isso significa é que...
Para saber a tensão normal nessa coluna, podemos fazer a superposição de efeitos desses três carregamentos (momento em , momento em , e compressão ) para encontrarmos que:
Sendo que normalmente essa fórmula é escrita reorganizada assim:
E o que é que o exercício quer?
Ele quer que a gente determine a tensão máxima nessa coluna.
Daí que observando a fórmula acima para , vemos que:
1. O termo vai ter um valor sempre de compressão (), uma vez que .
2. O termo assume seu valor máximo de compressão () para , no “topo da seção”, e seu valor máximo de tração () para , na “base da seção”.
& 3. O termo assume seu valor máximo de compressão () para , na “direita da seção”, e seu valor máximo de tração () para , na “esquerda da seção”.
Dessa forma, a tensão máxima nessa coluna vai ser uma tensão de compressão no ponto de sua seção de posição e :
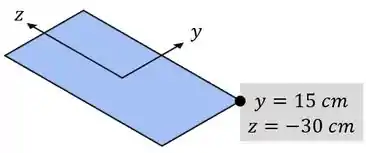
Isso porque esse é o único ponto em que vamos ter a...
- (1.) Compressão uniforme devido à força normal
- (2.) Compressão máxima devido à
- (3.) Compressão máxima devido à .
- Calcular os momentos e e o esforço interno normal gerados pela nossa carga excêntrica;
- Calcular as propriedades geométricas , e para a seção transversal da nossa coluna;
- & aplicar a fórmula para o ponto de compressão máxima na coluna.
Colaborando com a...
Colaborando com a...
Então, para resolver o exercício, devemos:
Passo 2
Agora que a gente já entendeu e revisou tudo que está rolando no exercício, podemos seguir direto para uma resolução bem rápida dele.
Primeiro, vamos calcular os momentos e e o esforço interno normal gerados pela nossa carga excêntrica.
Observando a nossa plataforma:
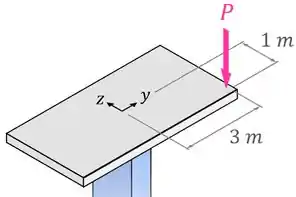
Vemos que o momento em relação ao eixo , vai ser gerado com um braço de e vai ter um valor positivo, por estar no sentido do eixo de acordo com a regra da mão direita.
Dessa forma, vamos ter que:
E também vemos que o momento vai ser gerado com um braço de e vai ter um valor positivo, por estar no sentido do eixo de acordo com a regra da mão direita.
Dessa forma, temos que:
Por fim, como a força é de compressão, ela vai gerar uma força interna normal :
Passo 3
Em seguida, vamos calcular as propriedades geométricas para seção transversal da coluna, observando as dimensões indicadas pelo exercício:
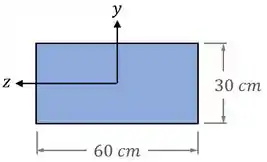
Quanto à área , temos:
Quanto ao momento de inércia da área em relação ao eixo , , vamos ter uma base (paralela à linha neutra no eixo ) e uma altura (perpendicular à linha neutra) .
Então:
Já para , o eixo da linha neutra troca e as dimensões também: a base paralela à linha neutra no eixo vai ser e a altura perpendicular à linha neutra vai ser :
Passo 4
Agora, só falta aplicar a fórmula:
...para o ponto de compressão máxima para encontrarmos a tensão normal máxima nessa coluna.
Aplicando essa fórmula e substituindo nela:
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- & ,
...vamos encontrar a nossa tensão normal máxima na coluna:
Calculando cada termo, temos:
E somando tudo, encontramos que:
Convertendo esse resultado para temos:
Aí, na hora de fornecer nosso resultado final, o fornecemos como um valor absoluto e indicamos que é uma tensão de compressão:
Resposta
Exercício Resolvido #3
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 285-4.103.
A parte vertical da prensa mostrada na figura consiste em um tubo retangular com espessura de parede . Sabendo que a prensa foi usada para prender blocos de madeira que estavam sendo colados, com uma força , determine a tensão no ponto e ponto .
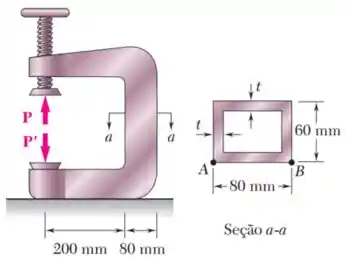
Passo 1
O que está acontecendo?
As cargas , em relação ao centro da parte vertical da prensa, são excêntricas por uma distância de , como mostra a imagem abaixo:
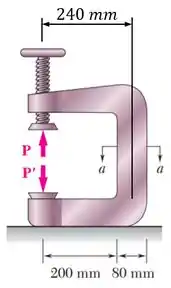
Dessa forma, definindo eixos e passando pelo centro da seção transversal dessa parte vertical:
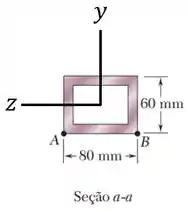
Vemos que a força excêntrica vai causar nessa seção transversal não só uma força normal como também um momento em relação ao eixo , :
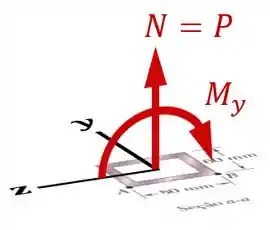
Sendo que esse momento é positivo ao longo do eixo de acordo com a regra da mão direita:

...e pode ser calculado multiplicando a força pela “excentricidade” ou pelo braço de :
E o que é que o exercício quer?
Ele quer que a gente determine a tensão nos pontos e dessa seção transversal .
Aí, pelo o que estudamos sobre cargas excêntricas, sabemos que elas geram uma tensão de acordo com a fórmula:
...dados que o eixos esteja disposto “para cima” e o eixo esteja disposto “para a esquerda” na seção transversal da peça, que foi como nós fizemos:
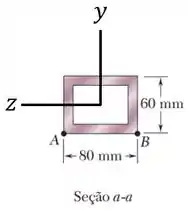
Como no nosso caso, não temos nenhum momento em relação ao eixo , a tensão nessa seção transversal vai ficar assim na realidade:
Sendo que da imagem acima, vemos que o ponto possui uma posição e que o ponto possui uma posição .
Dessa forma, para resolvermos o exercício, temos que:
1. Calcular a área e o momento de inércia da área em relação ao eixo , , dessa seção transversal, sabendo que ela possui uma espessura de parede ;
& 2. Aplicar a fórmula para os pontos e .
Passo 2
Então vamos lá!
Primeiro, observando a geometria da seção, com sua espessura :
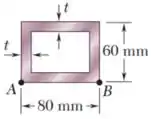
Vemos que ela é um retângulo de com um furo retangular de por .
Dessa forma, a sua área vai ser:
Passo 3
Em seguida, precisamos calcular o momento de inércia da área em relação ao eixo , , para essa seção.
Para tanto, vamos observar a sua geometria em relação ao eixo :
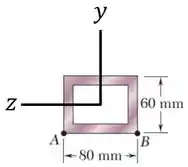
Em relação ao eixo , vemos que ela tem uma base (paralela ao eixo ) e uma altura (perpendicular ao eixo ) .
Dessa forma, o momento de inércia da área em relação ao eixo do retângulo externo dessa seção vai ser:
Mas a seção não tem só esse retângulo externo.
Ela também tem um furo, de base e altura (dimensões que vimos no passo anterior), que vai ter um momento de inércia negativo por ser um furo:
E assim, o momento de inércia da área da seção como um todo vai ser a soma dos valores de para cada elemento:
O que significa que:
Passo 4
Por fim, aplicamos a fórmula para os pontos e :
Substituindo nessas equações:
- ;
- ;
- ;
- & ;
- & ,
Vamos ter que:
Calculando tudo e sabendo que é o mesmo que , encontramos os nossos resultados finais:
Resposta
Exercício Resolvido #4
Elaboração própria
Deduza a fórmula de tensão normal total para o ponto B levando em consideração a figura dada abaixo. Leve em consideração os sinais e orientações dos vetores.
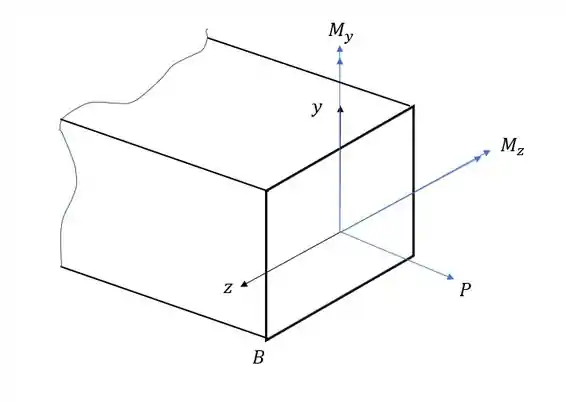
Passo 1
Para resolvermos essa questão temos que tomar cuidado com algumas coisas. A primeira é que temos 3 esforços nessa seção, dois esforços de flexão e um esforço normal, logo essa é a dica de que a nossa fórmula final deverá apresentar 3 parcelas, uma para cada esforço.
A segunda preocupação que devemos ter é com relação aos sinais, tanto dos eixos, quanto os dos momentos, além é claro das próprias fórmulas da flexão que apresentam os seus próprios sinais.
Por fim a última analise é um macete para verificarmos se acertamos ou não os sinais da fórmula.
Dito os cuidados precisamos lembrar das fórmulas de cada direção antes de começarmos de fato a resolver o exercício.
Sabemos que quando utilizamos o momento fletor direcionado no sentido de z usamos a fórmula
Quando utilizamos o momento fletor direcionado no sentido de Y usamos a fórmula
E por fim quando temos a ação de um esforço normal usamos a fórmula
Agora vamos entender a nossa solução.
Passo 2
Vamos analisar a ação de cada esforço separadamente, primeiro vamos analisar o momento fletor na direção Z.
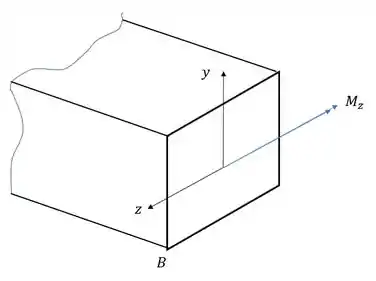
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto B.
Primeiro vemos que a direção do momento fletor é contrário ao eixo z, logo,
O sinal de Y é determinado pela posição do ponto que calculamos, nesse caso, em relação a Y o ponto B está em baixo.
Como arbitramos que Y é negativo pra baixo e positivo pra cima, teremos que
Como o momento de inercia não tem sinal, a parcela de contribuição devido no ponto B será
Passo 3
Agora vamos analisar a ação do esforço para o momento fletor na direção Y.
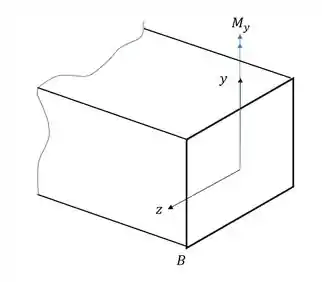
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto B.
Primeiro vemos que a direção do momento fletor é a mesma do eixo y, logo,
O sinal de Z é determinado pela posição do ponto que calculamos, nesse caso, em relação a Z o ponto B está na esquerda.
Como arbitramos que Z é negativo pra direita e positivo pra esquerda, teremos que
Como o momento de inercia não tem sinal, a parcela de contribuição devido no ponto B será
Passo 4
Por fim vamos analisar a parcela referente a ação do esforço normal
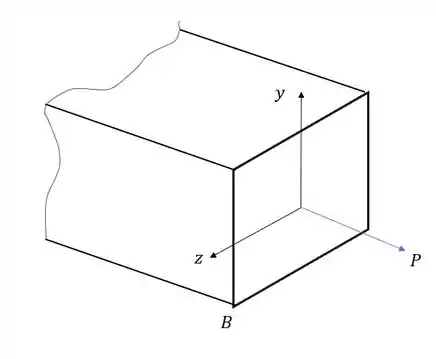
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto B.
Primeiro vemos que a direção do normal é a mesma do sentido de tração, logo,
Como a área não tem sinal, a parcela de contribuição devido no ponto B será
Passo 5
Agora que já determinamos todas as parcelas, basta somarmos todas elas na fórmula final, logo teremos que a tensão total normal será
Passo 6
Agora que já determinamos o valor de cada uma das contribuições de cada seção vamos usas o macete pra saber se todos os sinais que determinamos estão certinhos.
Vamos definir o seguinte, nenhuma das fórmulas possui sinal, log consideraremos tudo positivo, todos os sinais serão dados apenas pela analise de tração e compressão. Para isso vamos desenhar retângulos e os nossos momentos.
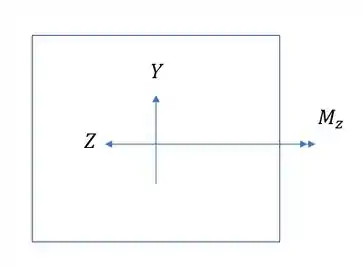
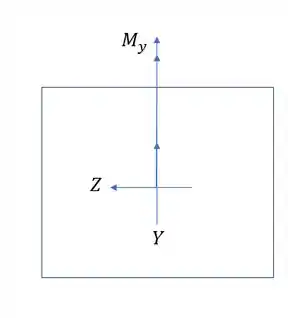
Agora só analisar quais regiões são tracionadas e quais são comprimidas
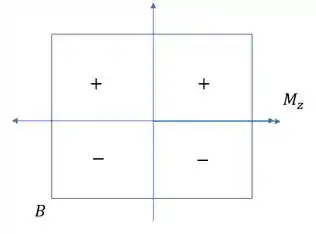
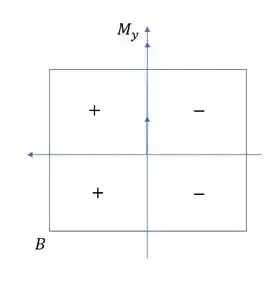
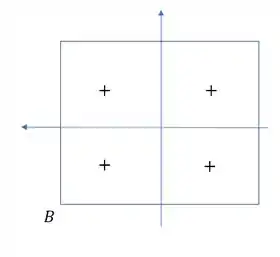
Se olharmos cada quadrante vemos que no primeiro caso B comprime, logo negativo, e nos outros dois casos traciona, ou seja, positivo.
Primeiro caso negativo
Segundo caso positivo
Terceiro caso positivo
Logo a nossa fórmula de tensões normais totais será
O que confirma que todo o cálculo que fizemos nos passos anteriores estão certinhos. Se por acaso o professor autorizar você pode usar somente o passo 6 dessa solução para resolver o problema, mas lembre-se, procure ver se o professor autoriza usar tal processo.
Resposta
Exercício Resolvido #5
Elaboração própria
A barra abaixo está sujeita aos momentos fletores mostrados na figura, determine a tensão normal nos pontos A e B da figura mostrada. A seção mostrada tem dimensão (50x50) cm.
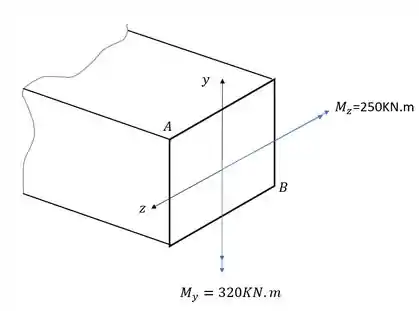
Passo 1
Para resolvermos essa questão temos que tomar cuidado com algumas coisas. A primeira é que temos 2 esforços nessa seção, os dois esforços de flexão, logo essa é a dica de que a nossa fórmula final deverá apresentar 2 parcelas, uma para cada esforço.
A segunda preocupação que devemos ter é com relação aos sinais, tanto dos eixos, quanto os dos momentos, além é claro das próprias fórmulas da flexão que apresentam os seus próprios sinais.
Dito os cuidados precisamos lembrar das fórmulas de cada direção antes de começarmos de fato a resolver o exercício.
Sabemos que quando utilizamos o momento fletor direcionado no sentido de z usamos a fórmula
Quando utilizamos o momento fletor direcionado no sentido de Y usamos a fórmula
Como a nossa seção é quadrada, já podemos determinar facilmente o valor do momento de inercia que será igual em ambas as direções, logo
Passo 2
Vamos analisar a ação de cada esforço separadamente, primeiro vamos analisar o momento fletor na direção Z.
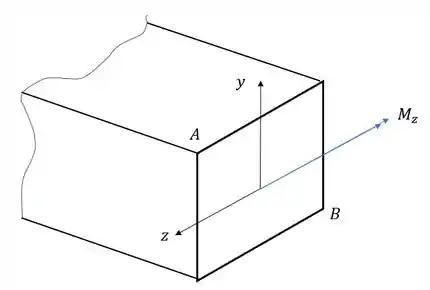
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto A e B.
Primeiro vemos que a direção do momento fletor é contrário ao eixo z, logo,
O sinal de Y é determinado pela posição do ponto que calculamos, nesse caso, em relação a Y o ponto B está em baixo e A está em cima.
Como arbitramos que Y é negativo pra baixo e positivo pra cima, teremos que
Como o momento de inercia não tem sinal, a parcela de contribuição devido no ponto A e B será
Passo 3
Agora vamos analisar a ação do esforço para o momento fletor na direção Y.
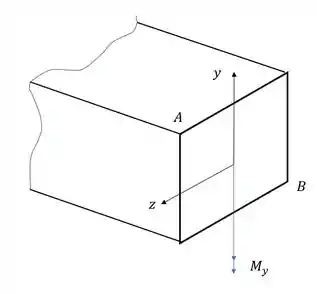
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto A e B.
Primeiro vemos que a direção do momento fletor é contrário ao eixo y, logo,
O sinal de Z é determinado pela posição do ponto que calculamos, nesse caso, em relação a Z o ponto B está na direita e A está na esquerda.
Como arbitramos que Z é negativo pra direita e positivo pra esquerda, teremos que
Como o momento de inercia não tem sinal, a parcela de contribuição devido no ponto A e B será
Passo 4
Agora que já determinamos todas as parcelas, basta somarmos todas elas na fórmula final, logo teremos que a tensão total Normal será
Resposta
Exercício Resolvido #6
Elaboração própria
Na ponta do pilar abaixo foi colocado uma carga concentrada (que representa a ação de uma viga ali apoiada). Com base em seus conhecimentos de cargas excêntricas determine a tensão normal no ponto A. O raio do pilar é de 0,80m.
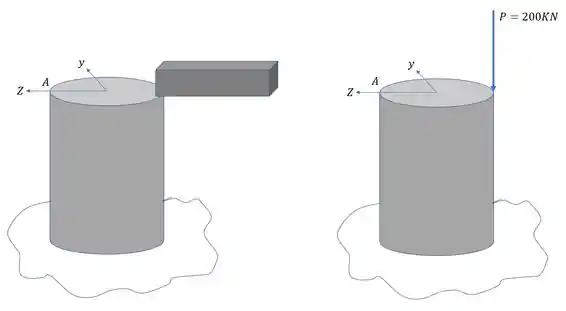
Passo 1
O primeiro passo que temos que dar é trocar as cargas mostradas por esforços e assim vermos qual fórmula usar.
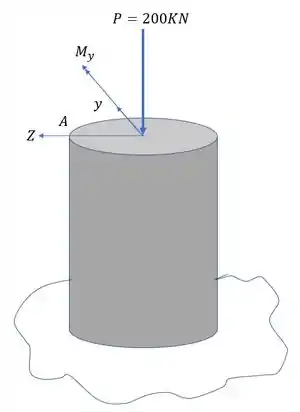
Aqui é importante ressaltar que levamos a carga P para o centro da peça e junto com ela o momento fletor causado por ela, que nesse caso é um momento fletor na direção y.
Como temos dois esforços, já sabemos que temos 2 parcelas para calcular.
Quando utilizamos o momento fletor direcionado no sentido de Y usamos a fórmula
E por fim quando temos a ação de um esforço normal usamos a fórmula
Como a nossa seção é circular, já podemos determinar facilmente o valor do momento de inercia que será igual em ambas as direções, logo
Agora vamos entender a nossa solução.
Passo 2
Agora vamos analisar a ação do esforço para o momento fletor na direção Y.
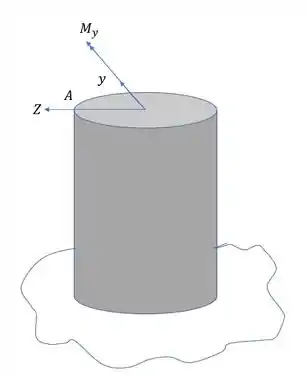
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto A.
Primeiro vemos que a direção do momento fletor é a mesma do eixo y, logo,
O sinal de Z é determinado pela posição do ponto que calculamos, nesse caso, em relação a Z o ponto A está na esquerda.
Como arbitramos que Z é negativo pra direita e positivo pra esquerda, teremos que
Como o momento de inercia não tem sinal, a parcela de contribuição devido no ponto B será
Passo 3
Por fim vamos analisar a parcela referente a ação do esforço normal
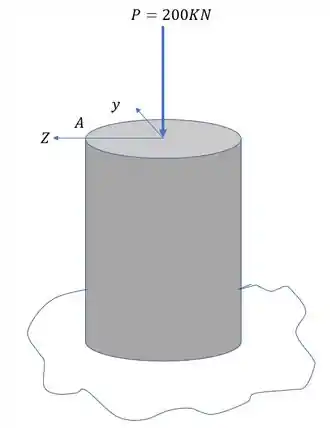
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto B.
Primeiro vemos que a direção do normal é a mesma do sentido de compressão, logo,
Como a área não tem sinal, a parcela de contribuição devido no ponto B será
Passo 4
Agora que já determinamos todas as parcelas, basta somarmos todas elas na fórmula final, logo teremos que a tensão total Normal será
Resposta
Exercício Resolvido #7
Elaboração própria
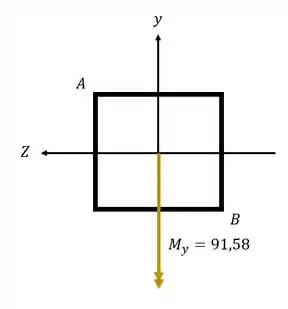
Uma barra está sujeita aos esforços mostrados abaixo, determine a tensão normal no ponto B. diga se essa tensão é de tração ou de compressão.
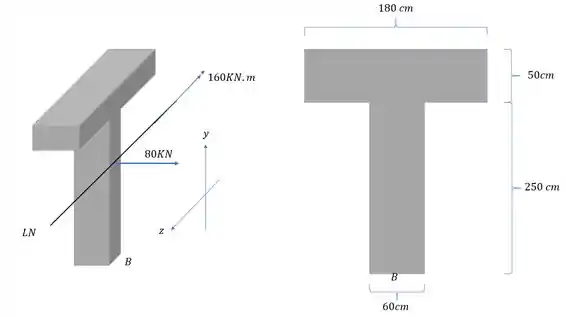
Passo 1
Para resolvermos essa questão temos que tomar cuidado com algumas coisas. A primeira é que temos 2 esforços nessa seção, um esforço de flexão e um normal, logo essa é a dica de que a nossa fórmula final deverá apresentar 2 parcelas, uma para cada esforço.
A segunda preocupação que devemos ter é com relação aos sinais, tanto dos eixos, quanto os dos momentos, além é claro das próprias fórmulas da flexão que apresentam os seus próprios sinais.
Dito os cuidados precisamos lembrar das fórmulas de cada direção antes de começarmos de fato a resolver o exercício.
Sabemos que quando utilizamos o momento fletor direcionado no sentido de z usamos a fórmula
E por fim quando temos a ação de um esforço normal usamos a fórmula
Passo 2
Com relação ao valor de Y teremos que descobrir a posição da linha neutra, para isso teremos que fazer o nosso passo a passo
Primeiro determinamos a origem do nosso sistema

Agora vamos dividir a nossa peça em dois elementos mais simples
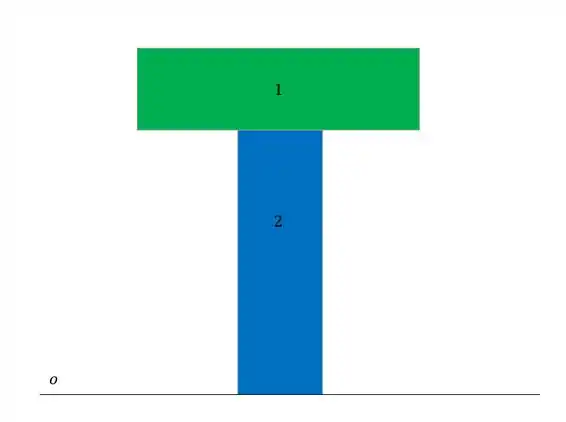
Em seguida descobrimos quanto vale a área e a distância do centroide de cada elemento até a nossa origem.
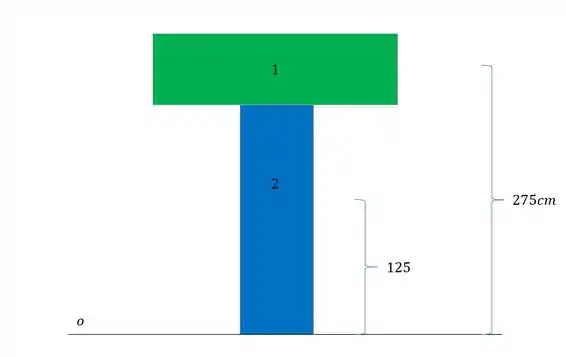
Dessa forma descobrimos facilmente que as áreas serão
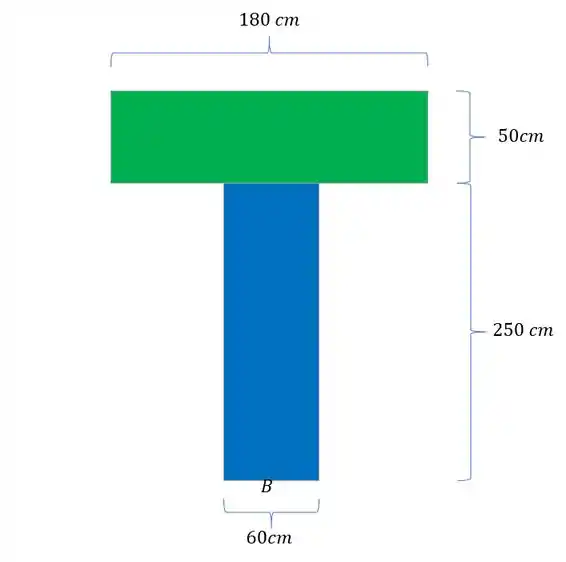
Definimos assim a nossa linha neutra
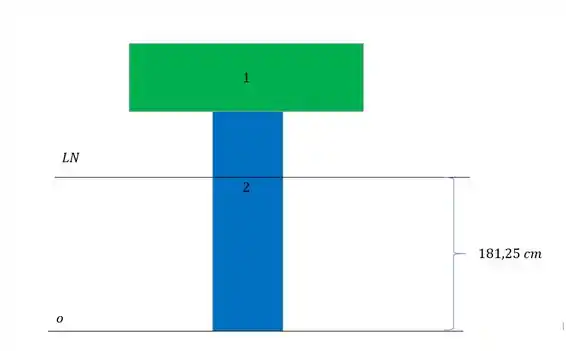
Agora só falta o momento de inércia
Passo 3
Para o cálculo do momento de inércia teremos que usar de novo o nosso passo a passo. Sabemos que para calcularmos momentos de inercia precisamos determinar 3 coisas. As áreas de cada elemento, a distância do centroide de cada elemento até a linha neutra e por fim o momento de inercia de cada elemento. Como os elementos são retangulares, teremos que o momento de inercia deles é
A figura abaixo representa as distâncias dos centroides de cada elemento até a linha neutra
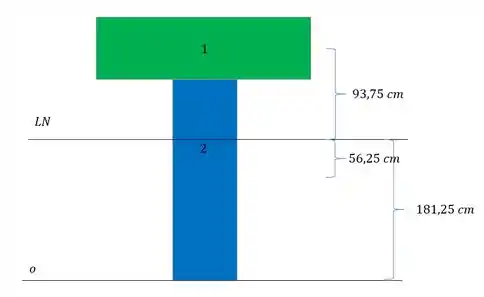
E nessa imagem temos as medidas para calcularmos os momentos de inercia
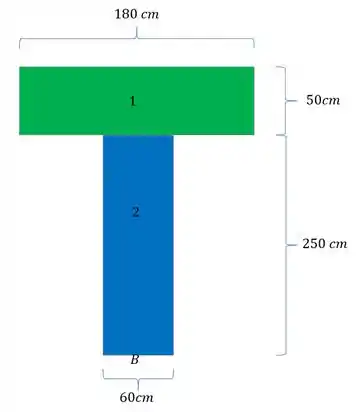
Calculando o momento de inercia de cada elemento teremos que
E no passo anterior já tínhamos determinado o valor das áreas
Agora que já temos todos os valores, bata calcularmos o momento de inercia para a fórmula
Passo 4
Vamos analisar a ação de cada esforço separadamente, primeiro vamos analisar o momento fletor na direção Z.
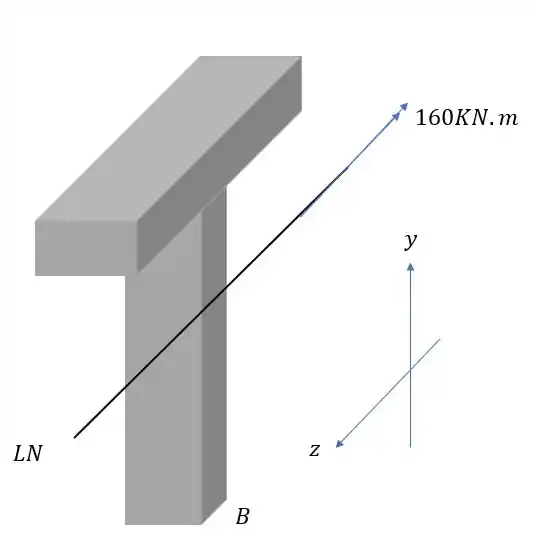
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto B.
Primeiro vemos que a direção do momento fletor é contrário ao eixo z, logo,
O sinal de Y é determinado pela posição do ponto que calculamos, nesse caso, em relação a Y o ponto B está em baixo.
Como arbitramos que Y é negativo pra baixo e positivo pra cima, teremos que Y valerá a própria distancia que encontramos para a linha neutra.
Como o momento de inercia não tem sinal, a parcela de contribuição devido no ponto B será
Passo 5
Por fim vamos analisar a parcela referente a ação do esforço normal
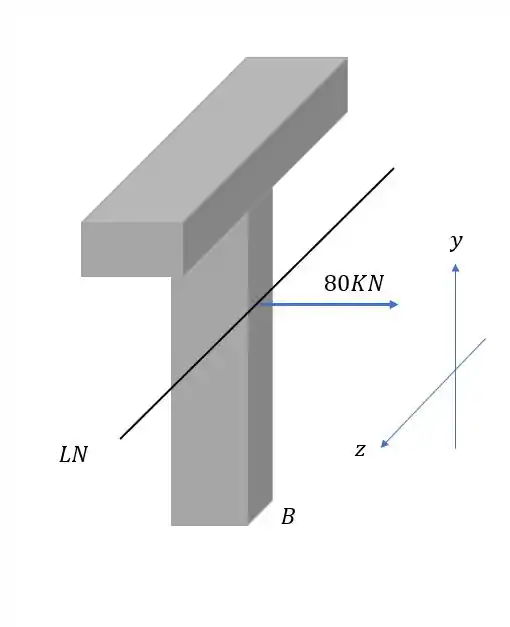
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto B.
Primeiro vemos que a direção do normal é a mesma do sentido de tração, logo,
Como a área não tem sinal, a parcela de contribuição devido no ponto B será
Passo 6
Agora que já determinamos todas as parcelas, basta somarmos todas elas na fórmula final, logo teremos que a tensão total Normal será
Resposta
A tensão é de compressão
Exercício Resolvido #8
Elaboração própria
A seção quadrada abaixo, de lado 33cm, está sujeita a flexão assimétrica mostrada na figura. Usando seu conhecimento de decomposição vetorial, e seu conhecimento sobre tensão normal devido a flexão, determine o valor dos esforços normais no ponto A e B da peça.
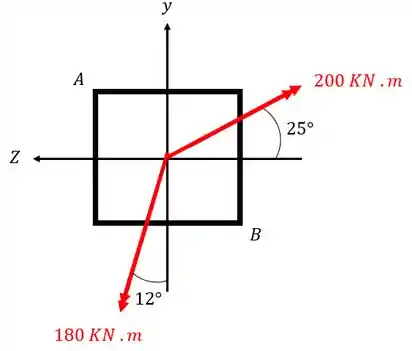
Passo 1
Para resolvermos essa questão temos que tomar cuidado com algumas coisas. A primeira é que temos 2 esforços nessa seção, os dois esforços de flexão, logo essa é a dica de que a nossa fórmula final deverá apresentar 2 parcelas, uma para cada esforço.
A segunda preocupação que devemos ter é com relação aos sinais, tanto dos eixos, quanto os dos momentos, além é claro das próprias fórmulas da flexão que apresentam os seus próprios sinais.
Dito os cuidados precisamos lembrar das fórmulas de cada direção antes de começarmos de fato a resolver o exercício.
Sabemos que quando utilizamos o momento fletor direcionado no sentido de z usamos a fórmula
Quando utilizamos o momento fletor direcionado no sentido de Y usamos a fórmula
Como a nossa seção é quadrada, já podemos determinar facilmente o valor do momento de inercia que será igual em ambas as direções, logo
Passo 2
Do jeito que os momentos fletores estão é muito complicado definir as fórmulas e os cálculos que devemos fazer, por isso, antes de qualquer coisa, vamos decompor os nossos momentos fletores, e com essa decomposição vamos poder analisar os nossos esforços.
Vamos decompor cada um dos vetores, começando pelo de
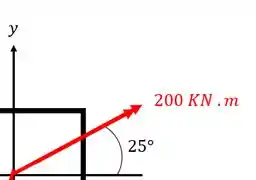
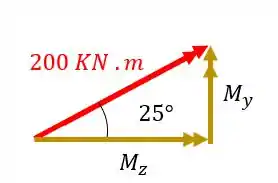
Fazendo a conta teremos que
Isolando teremos que
Decompondo agora o momento de teremos
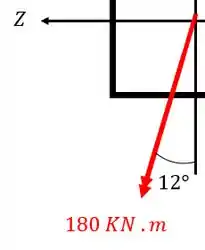
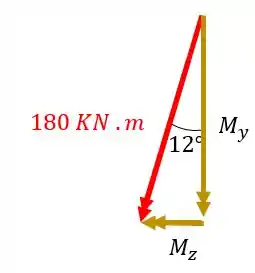
Fazendo a conta teremos que
Isolando teremos que
Olhando os vetores decompostos teremos que
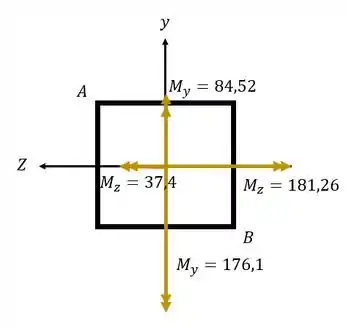
Fazendo uma soma vetorial teremos que
Então teremos
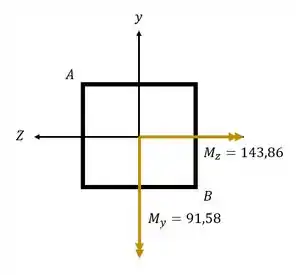
Passo 3
Vamos analisar a ação de cada esforço separadamente, primeiro vamos analisar o momento fletor na direção Z.
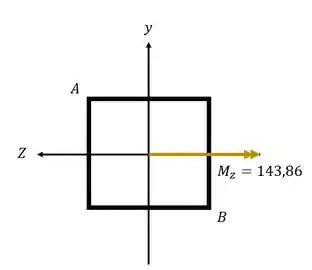
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto A e B.
Primeiro vemos que a direção do momento fletor é contrário ao eixo z, logo,
O sinal de Y é determinado pela posição do ponto que calculamos, nesse caso, em relação a Y o ponto B está em baixo e A está em cima.
Como arbitramos que Y é negativo pra baixo e positivo pra cima, teremos que
Como o momento de inercia não tem sinal, a parcela de contribuição devido no ponto A e B será
Passo 4
Agora vamos analisar a ação do esforço para o momento fletor na direção Y.
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto A e B.
Primeiro vemos que a direção do momento fletor é contrário ao eixo y, logo,
O sinal de Z é determinado pela posição do ponto que calculamos, nesse caso, em relação a Z o ponto B está na direita e A está na esquerda.
Como arbitramos que Z é negativo pra direita e positivo pra esquerda, teremos que
Como o momento de inercia não tem sinal, a parcela de contribuição devido no ponto A e B será
Passo 5
Agora que já determinamos todas as parcelas, basta somarmos todas elas na fórmula final, logo teremos que a tensão total Normal será
Resposta
Exercício Resolvido #9
Elaboração própria
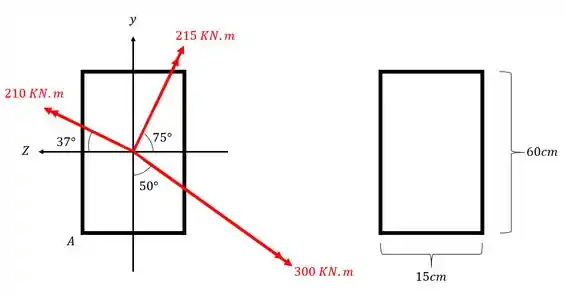
Uma viga de um prédio sofreu um recalque no apoio e a sua seção transversal foi sujeita ao carregamento assimétrico mostrado abaixo. Determine o valor da tensão normal no ponto A da figura.
Passo 1
Para resolvermos essa questão temos que tomar cuidado com algumas coisas. A primeira é que temos 2 esforços nessa seção, os dois esforços de flexão, logo essa é a dica de que a nossa fórmula final deverá apresentar 2 parcelas, uma para cada esforço.
A segunda preocupação que devemos ter é com relação aos sinais, tanto dos eixos, quanto os dos momentos, além é claro das próprias fórmulas da flexão que apresentam os seus próprios sinais.
Dito os cuidados precisamos lembrar das fórmulas de cada direção antes de começarmos de fato a resolver o exercício.
Sabemos que quando utilizamos o momento fletor direcionado no sentido de z usamos a fórmula
Quando utilizamos o momento fletor direcionado no sentido de Y usamos a fórmula
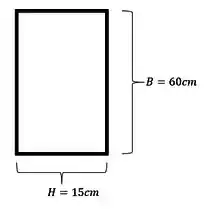
Como a nossa seção é retangular, teremos que determinar o momento de inercia para cada direção, então teremos
Para o
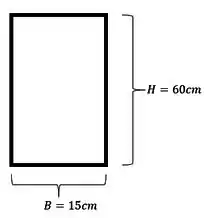
Para o
Passo 2
Do jeito que os momentos fletores estão é muito complicado definir as fórmulas e os cálculos que devemos fazer, por isso, antes de qualquer coisa, vamos decompor os nossos momentos fletores, e com essa decomposição vamos poder analisar os nossos esforços.
Vamos decompor cada um dos vetores, começando pelo de
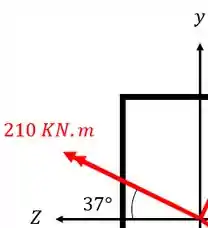
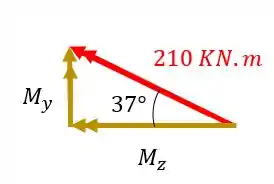
Fazendo a conta teremos que
Isolando teremos que
Decompondo agora o momento de teremos
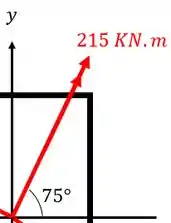
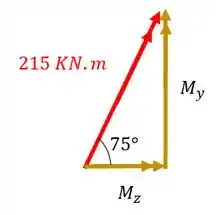
Fazendo a conta teremos que
Isolando teremos que
Decompondo agora o momento de teremos
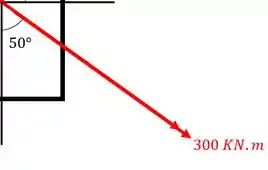
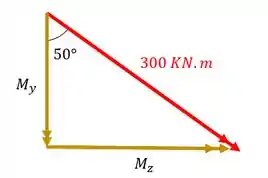
Fazendo a conta teremos que
Isolando teremos que
Olhando os vetores decompostos teremos que
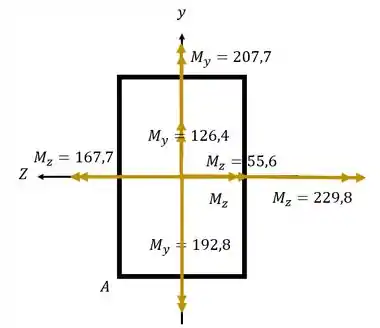
Fazendo uma soma vetorial teremos que
Então teremos

Passo 3
Vamos analisar a ação de cada esforço separadamente, primeiro vamos analisar o momento fletor na direção Z.
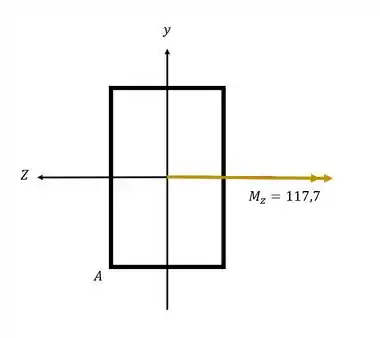
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto A .
Primeiro vemos que a direção do momento fletor é contrário ao eixo z, logo,
O sinal de Y é determinado pela posição do ponto que calculamos, nesse caso, em relaç��o a Y o ponto A está em baixo.
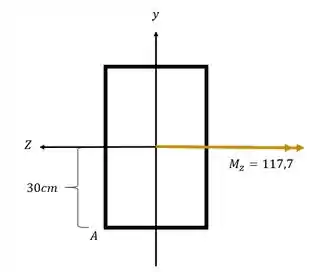
Como arbitramos que Y é negativo pra baixo e positivo pra cima, teremos que
Como o momento de inercia não tem sinal, a parcela de contribuição devido no ponto A será
Passo 4
Agora vamos analisar a ação do esforço para o momento fletor na direção Y.
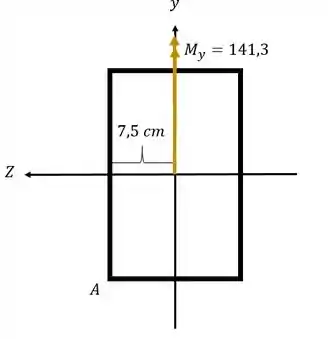
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto A e B.
Primeiro vemos que a direção do momento fletor é contrário ao eixo y, logo,
O sinal de Z é determinado pela posição do ponto que calculamos, nesse caso, em relação a Z o ponto A está na esquerda.
Como arbitramos que Z é negativo pra direita e positivo pra esquerda, teremos que
Como o momento de inercia não tem sinal, a parcela de contribuição devido no ponto A será
Passo 5
Agora que já determinamos todas as parcelas, basta somarmos todas elas na fórmula final, logo teremos que a tensão total Normal será
Resposta
Exercício Resolvido #10
Elaboração própria
Uma viga de seção furada está sujeita ao carregamento mostrado abaixo. Sabendo disso determine o valor da tensão normal no ponto A da figura.
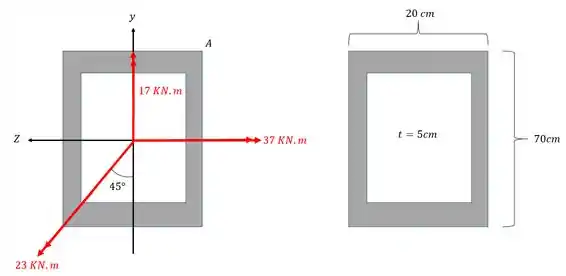
Passo 1
Para resolvermos essa questão temos que tomar cuidado com algumas coisas. A primeira é que temos 2 esforços nessa seção, os dois esforços de flexão, logo essa é a dica de que a nossa fórmula final deverá apresentar 2 parcelas, uma para cada esforço.
A segunda preocupação que devemos ter é com relação aos sinais, tanto dos eixos, quanto os dos momentos, além é claro das próprias fórmulas da flexão que apresentam os seus próprios sinais.
Dito os cuidados precisamos lembrar das fórmulas de cada direção antes de começarmos de fato a resolver o exercício.
Sabemos que quando utilizamos o momento fletor direcionado no sentido de z usamos a fórmula
Quando utilizamos o momento fletor direcionado no sentido de Y usamos a fórmula
Como a nossa seção é retangular, teremos que determinar o momento de inercia para cada direção. Aqui também temos que tomar cuidado pois precisamos fazer uma diferença entre o momento de inercia da seção cheia subtraída do momento de inercia da seção vazada como mostra o exemplo abaixo
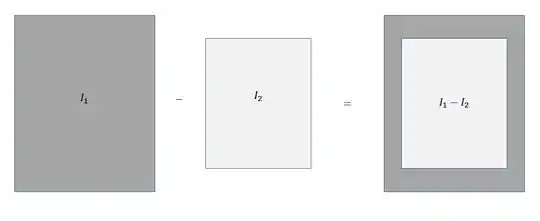
Para o
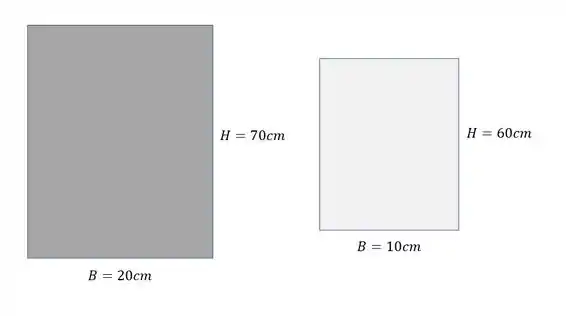
Para o
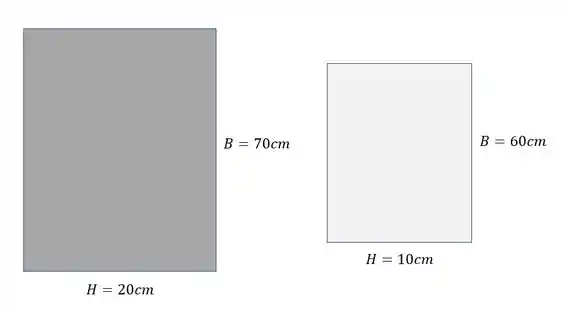
Passo 2
Do jeito que os momentos fletores estão é muito complicado definir as fórmulas e os cálculos que devemos fazer, por isso, antes de qualquer coisa, vamos decompor os nossos momentos fletores, e com essa decomposição vamos poder analisar os nossos esforços.
Como só temos um vetor fora do eixo principal, somente ele que vamos decompor
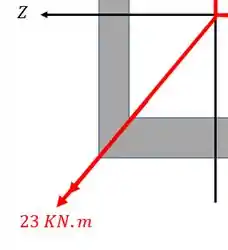
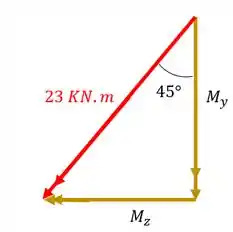
Fazendo a conta teremos que
Isolando teremos que
Olhando os vetores decompostos teremos que
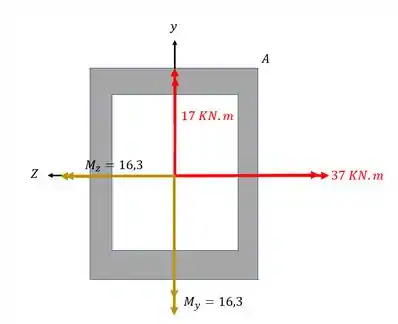
Fazendo uma soma vetorial teremos que
Então teremos
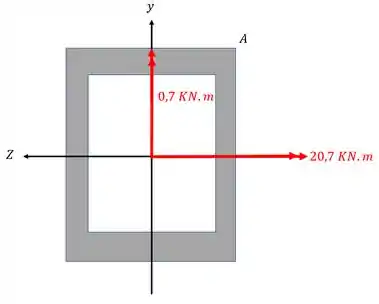
Passo 3
Vamos analisar a ação de cada esforço separadamente, primeiro vamos analisar o momento fletor na direção Z.
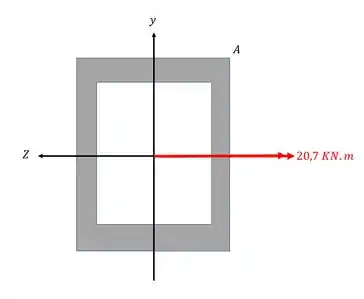
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto A.
Primeiro vemos que a direção do momento fletor é contrário ao eixo z, logo,
O sinal de Y é determinado pela posição do ponto que calculamos, nesse caso, em relação a Y o ponto A está em cima.
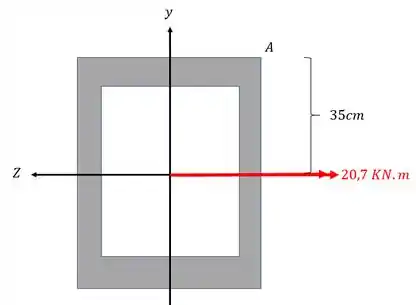
Como arbitramos que Y é negativo pra baixo e positivo pra cima, teremos que
Como o momento de inercia não tem sinal, a parcela de contribuição devido no ponto A será
Passo 4
Agora vamos analisar a ação do esforço para o momento fletor na direção Y.
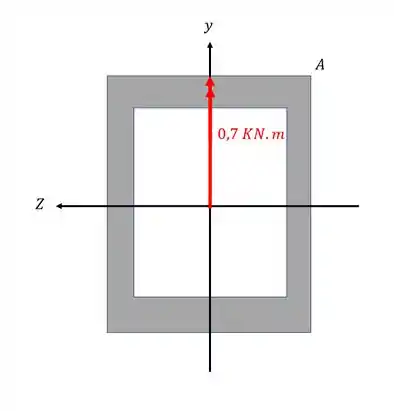
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto A e B.
Primeiro vemos que a direção do momento fletor é contr��rio ao eixo y, logo,
O sinal de Z é determinado pela posição do ponto que calculamos, nesse caso, em relação a Z o ponto A está na direita.
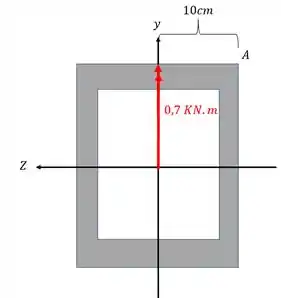
Como arbitramos que Z é negativo pra direita e positivo pra esquerda, teremos que
Como o momento de inercia não tem sinal, a parcela de contribuição devido no ponto A será
Passo 5
Agora que já determinamos todas as parcelas, basta somarmos todas elas na fórmula final, logo teremos que a tensão total Normal será