Fórmula da Flexão
Teoria
Introdução
Agora, vamos dizer que uma questão da sua prova pede que você determine a tensão máxima devido à flexão na viga em “T” abaixo:
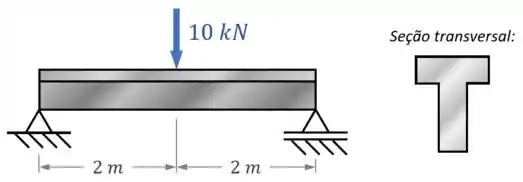
Como você resolve esse exercício?
Bom...
O primeiro passo pode ser aplicar os métodos da estática (DCL, equilíbrio, análise dos esforços internos e diagramas de esforços internos) para essa viga.
Fazendo isso, você vai encontrar esforços internos nessa viga na forma de forças cortantes e momentos fletores .
Você pode encontrar, por exemplo, que na seção transversal crítica dessa viga, bem no meio dela, ela está submetida a uma força cortante e a um momento fletor máximo :
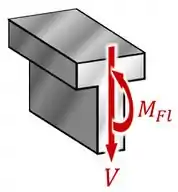
E aí aqui a coisa complica...
Porque a gente até já viu:
- Lá em “cargas axiais”, como descrever as tensões causadas pela tração ou compressão de uma força normal ;
- E lá em “torção”, como descrever as tensões geradas pela torção de um torque interno (ou momento torsor , para alguns professores);
E, depois, a gente até vai ver:
- No próximo assunto, de “cisalhamento”, como calcular as tensões devido à força cortante numa peça.
Mas aqui e agora, nós precisamos saber como é a tensão que é gerada pela flexão de um momento fletor :
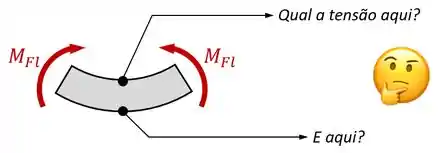
E a gente realmente precisa saber descrever essa tensão!!
Isso porque (spoiler!) a falha da maioria das estruturas em Resistência dos Materiais e na vida real acontece por causa da tensão de flexão de um momento fletor.
Então... fica a pergunta:
Como é & como calculamos a tensão criada por um momento fletor?
Fórmula da Flexão
A primeira coisa que podemos observar é que um momento fletor aplicado em um elemento de uma peça comprime algumas “fibras” desse elemento e estica/traciona outras:
Então, como tração e compressão estão reclacionados à existência de tensões normais , isso significa que o momento fletor gera tensões normais em uma peça!
Aí uma galera estudou essa tração/compressão devido ao momento e descobriu que a tensão normal gerada pelo momento fletor é descrita pela fórmula:
Que é chamada de fórmula da flexão, onde:
- (ou só “” para alguns professores) é o momento fletor em uma seção da peça;
- é a posição do ponto em que se quer calcular a tensão em relação à centroide/linha neutra da seção transversal da peça;
- & (ou só “”) é uma propriedade geométrica da seção transversal, chamada de momento de inércia da área.
Beleza...
Mas o que é que essa fórmula significa?
Olhando para ela e considerando um momento fletor positivo (), vemos que:
1. Para valores positivos () de (ou seja, em pontos acima da centroide/linha neutra da seção transversal da peça), a tensão normal vai ter valores negativos (), de compressão;
Enquanto que...
2. Para valores negativos () de (ou seja, em pontos abaixo da centroide/linha neutra), a tensão vai ter valores positivos (), de tração.
Além disso...
Olhando para ela, também vemos que:
3. A tensão cresce linearmente a medida que a posição relativa à linha neutra aumenta;
& 4. A tensão é nula quando , ou seja, a tensão é nula na linha neutra.
Tudo isso significa que se fossemos visualizar as tensões devido à flexão em uma seção transversal da nossa viga em “T”, veríamos algo assim:
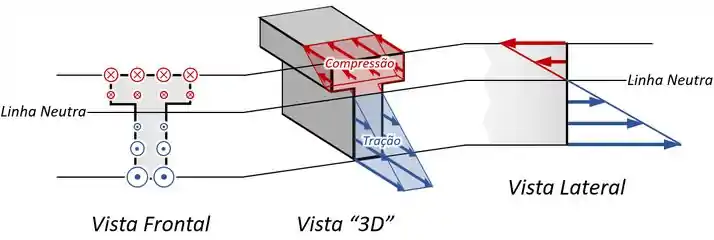
Sendo que, caso o momento fletor fosse negativo (), o contrario aconteceria: teríamos uma tração nas partes da seção acima da linha neutra e uma compressão nas partes abaixo.
E como é que eu uso essa fórmula?
Para usar ela para descobrir as tensões em uma seção a partir do momento fletor nela, nós precisamos fazer algumas coisas primeiro, que são:
A. Determinar a posição da linha neutra na sua seção transversal;
& B. Calcular o momento de inércia da área da seção;
Aí, depois de fazer esses dois passos, nós vamos poder definir os pontos da seção nos quais queremos calcular as tensões e fazer esse cálculo.
Então vamos aprender como fazer essas duas coisas!
A. Posição da Linha Neutra
Aqui, existem duas possibilidades.
A primeira é que a seção transversal da sua viga seja simétrica em relação à horizontal, como nos exemplos abaixo:
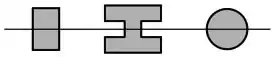
Nesses casos, a sua linha neutra vai ser essa linha de simetria.
Ou seja, você pode determinar a posição da linha neutra simplesmente dividindo por 2 a altura da sua seção.
A segunda é que a sua seção não seja simétrica em relação à horizontal.
Nesses casos, você terá que separar a viga em elementos numerados (normalmente retângulos ou círculos) e definir uma posição “” na base da viga:
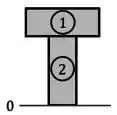
Feito isso, você deve usar as dimensões que o exercício forneceu para calcular:
- As áreas (, , etc.) de cada elemento;
- E as posições dos centros (, , etc.) de cada elemento, contadas a partir da posição “” definida.
Feito isso, você pode aplicar a fórmula abaixo:
Que é tipo uma média das posições dos centros de cada elemento ponderada com as áreas de cada um.
Assim, através dessa fórmula, você consegue determinar a posição da sua linha neutra, representada por (“y barra”):
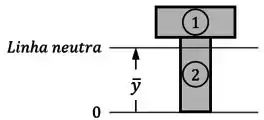
B. Momento de Inércia da Área
Aqui, mais uma vez, existem duas possibilidades.
A primeira é que a forma da sua seção seja uma forma simples, como um retângulo ou um círculo.
Nesse caso, você pode calcular o momento e inércia da área (ou só “”) usando as fórmulas:
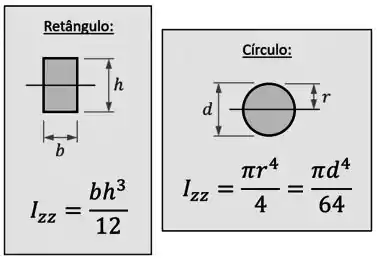
A segunda é que a forma da sua seção seja mais complexa e você tenha que separar ela em elementos numerados retangulares ou circulares, como já fizemos um pouco acima para a nossa viga em “T”.
Nesse caso, você deve:
- Usando as fórmulas acima, calcular os momentos de inércia da área (, , etc.) de cada elemento;
- Caso você ainda não tenha feito isso, calcular as áreas (, , etc.) de cada elemento;
- E, usando a posição da linha neutra que você encontrou anteriormente, calcular as distâncias (, , etc.) do centro de cada elemento até a linha neutra:
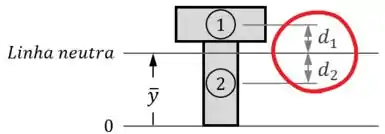
Feito tudo isso, você pode determinar o momento de inércia da área da sua seção transversal como um todo aplicando a fórmula abaixo:
Que é um somatório dos momento de inércia da área de cada elemento, mas levando também em consideração o teorema dos eixos paralelos.
Cálculo das Tensões
Finalmente, depois de determinar e , podemos calcular as tensões na nossa seção.
Nesse momento, normalmente o maior interesse está em calcular as tensões máximas de tração e compressão em uma seção.
Então, como queremos determinar as tensões normais de flexão:
...máximas positiva (, de tração) e negativa (, de compressão), devemos usar os valores máximos positivo e negativo da posição “” em relação à linha neutra.
Sendo que esses valores máximos de ocorrem sempre para o topo e para a base de uma seção.
Por exemplo:
Caso a gente tenha uma seção com altura total de e altura da linha neutra , os valores máximos positivo e negativo de vão ser:
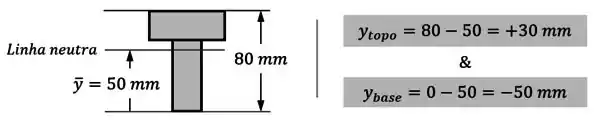
E pronto!
Substituindo na fórmula da flexão os valores de , e ou , vamos encontrar as tensões máximas de flexão na nossa viga!
Agora, você já está preparado para fazer uns exercícios resolvidos de flexão aqui, para depois mandar bem na sua prova.
Vamos lá? 👯
Fórmula da Flexão
A. Posição da Linha Neutra
B. Momento de Inércia da Área
Cálculo das Tensões
Exercícios Resolvidos
Exercício Resolvido #1
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 211-6.56. (Adaptado)
A viga é composta por três tábuas de madeira pregadas como mostra a figura. Se o momento que age na seção transversal for , determine a tensão de flexão máxima na viga. Faça um rascunho da distribuição de tensão que age na seção transversal.
Dica do Expert: Determine a posição da linha neutra da viga, depois calcule o momento de inércia da área da viga, e, por último, aplique a fórmula da flexão.
Passo 1
O que está acontecendo?
O momento aplicado vai gerar na seção transversal da viga uma tensão normal de flexão que é descrita pela fórmula da flexão:
Onde:
- (ou ) é o momento fletor aplicado na seção transversal;
- é a posição ponto onde se quer calcular a tensão de flexão em relação à linha neutra (ou eixo neutro) da viga;
- & (ou ) é o momento de inércia da área da seção transversal da viga em relação à sua linha neutra.
E o que é que o exercício quer?
Ele quer que a gente determine a tensão de flexão máxima nessa viga.
Então...
Para resolver o exercício, nós vamos ter que:
1. Determinar a posição da linha neutra.
Para fazer isso, podemos fazer uma média das posições dos centros de cada tábua de madeira ponderadas de acordo com as áreas de cada tábua:
Sendo que uma das formas de identificar os termos e dessa equação consiste em numerar cada tábua da viga e preencher uma tabela como a da figura abaixo:
Feito isso, podemos seguir para os próximos passos, que são:
2. Calcular o momento de inércia da área para essa viga.
Para fazer isso, vamos ter que nos lembrar:
- Que o momento de inércia da área de cada tábua retangular é , onde é a base da tábua (paralela à linha neutra) e é a sua altura (perpendicular à linha neutra);
- E que, devido ao teorema dos eixos paralelos, o momento de inércia da área da viga vai ser:
Onde é a distância do centro de cada tábua até a linha neutra .
& 3. Indicar o valor máximo absoluto de e calcular a tensão de flexão máxima absoluta, resolvendo assim o exercício.
Sendo que o valor máximo de vai ocorrer sempre ou para o topo ou para a base da viga.
Ao final de tudo, o exercício ainda quer que a gente faça um rascunho da distribuição de tensão que ocorre na seção transversal da viga.
Então sim... Eu sei... Parece muita coisa.
Mas segura aí que você consegue! 👊
Passo 2
Então vamos começar determinando a posição da linha neutra.
Para tanto, temos que olhar para a figura original do exercício:
Numerar as 3 tábuas da viga e identificar a base da viga como a posição :
E preencher, em uma tabela, o valor das áreas e das posições dos centros de cada tábua, além do produto desses valores para cada tábua:
Por último, fazemos o somatório das áreas e dos produtos e colocamos esses resultados na última linha da tabela:
Com isso, podemos finalmente calcular a posição da linha neutra:
E com isso, do exercício já está resolvido.
Nada mal, hein?
Passo 3
Agora, vamos calcular o momento de inércia da área para essa viga.
Sabemos que o momento de inércia da área de cada retângulo ou tábua que compõe a viga vai ser dado por:
Então vamos pensar...
Para a tábua 1, nós temos uma base de e uma altura de , então:
Para a tábua 2, e , então:
E para a tábua 3, e , logo:
Em seguida, temos que cada tábua tem uma distância entre o seu centro e a linha neutra da viga:
Para a tábua 1, que tem um centro com uma altura de , essa distância vai dar:
Já para a tábua 2, com seu centro com uma altura de , temos que:
E para a tábua 3, com um centro de altura de , temos:
Com isso, já definimos:
- Todos os momentos de inércia da área de cada tábua;
- Todas as distâncias de cada tábua;
- E todas as áreas de cada tábua, dispostas na tabela do passo anterior.
Então agora, só nos falta aplicar a fórmula:
E realizar esse somatório para encontrarmos o valor final de para essa viga:
Calculando tudo isso, encontramos que:
E assim, metade do exercício está resolvido!
Segura aí que tá acabando!
Passo 4
Por fim, podemos ver que, em termos absolutos, a posição em relação à linha neutra é maior para os pontos na base da nossa viga:
Do que para os pontos no topo da viga:
Ou seja, o valor máximo de (em termos absolutos) é:
E a tensão de flexão máxima na viga (em termos absolutos) é:
Daí que, substituindo:
- ;
- ;
- & ,
Temos que:
Simplificando tudo, isso fica assim:
Finalmente, calculando tudo e sabendo que é o mesmo que , encontramos que:
E olha só! Já temos a resposta do exercício!
Agora só falta o rascunho da distribuição de tensões na seção transversal.
Passo 5
Sobre essa distribuição de tensões na seção transversal da nossa viga, podemos dizer:
- Que ela varia linearmente com a variação da posição do ponto sendo estudado, como mostra a fórmula da flexão ;
- Que a posição da linha neutra em relação à ela mesmo é zero, e, portanto, na linha neutra;
- E que na base da viga, .
Se conseguirmos calcular também a tensão nos pontos do topo da viga, vamos ter informações suficientes para fazer o rascunho da distribuição de tensões.
Então vamos calcular a tensão nos pontos do topo da viga:
Substituindo:
- ;
- ;
- & ,
Encontramos que:
Com isso, considerando um eixo começando na base da viga, podemos marcar os pontos:
- para a base da viga, onde ;
- para a linha neutra, onde ;
- & para o topo da viga, onde ;
Conectando esses pontos por uma reta, conseguimos fazer o rascunho da distribuição de tensões abaixo:
E pronto!
Terminamos o exercício.
Resposta
Exercício Resolvido #2
Elaboração Própria
A viga representada na imagem está sofrendo um momento .
Determine a posição da linha neutra da seção transversal da viga.
Determine o momento de inércia da área seção transversal da viga.
Calcule as tensões máximas de tração e compressão na viga.
Represente em um gráfico a distribuição de tensão em uma seção transversal da viga.
Dica do Expert: O furo circular pode ser considerado como um elemento com uma área negativa e um momento de inércia da área negativo.
Passo 1
O que está acontecendo?
A viga retangular, de base e altura , tem um furo de diâmetro (e, consequentemente, raio .)
É aplicada nela um momento , o que causa nela tensões normais de flexão dadas pela fórmula da flexão:
Onde:
- é a posição do ponto em que se quer avaliar a tensão de flexão em relação à linha neutra da viga;
- & é o momento de inércia da área da seção transversal dessa viga.
E o que é que o exercício quer?
Primeiro, no item , ele quer saber a posição da linha neutra da seção transversal dessa viga, que pode ser encontrada usando a fórmula:
Sendo que uma forma de identificar os termos e dessa equação é numerar o retângulo e o furo da viga e preencher uma tabela como a da figura abaixo:
Lembrando que precisamos considerar que o item possui uma área negativa, por se tratar de um furo.
Em seguida, no item , ele quer que a gente calcule o momento de inércia da área para a seção transversal dessa viga.
Para tanto, devemos lembrar:
1. As fórmulas de para elementos retangulares e circulares:
2. Que o valor final de para a viga vai ser dado por:
Onde é o valor de para cada elemento que compõe a viga, a área e a distância do centro de cada elemento (de posição ) à linha neutra (de posição ).
& 3. Que o momento de inércia da área e a área de um furo devem ser contabilizados como negativos.
Depois, no item , o exercício quer que a gente calcule as tensões de flexão máximas de tração () e de compressão () na viga.
Essas tensões máximas ocorrem no topo e na base da seção, que são os pontos com o maior valor positivo e negativo, respectivamente, da posição em relação à linha neutra.
Por último, no item , precisamos desenhar como fica a distribuição de tensões em uma seção transversal dessa viga, o que pode ser feito aproveitando os resultados do item .
Passo 2
Começando pelo item ...
Para determinar a posição da linha neutra, podemos olhar para a figura original do exercício:
Numerar os elementos que compõem a seção transversal dessa viga e identificar a base da viga como a posição :
E preencher, em uma tabela, o valor das áreas , das posições dos centros e do produto desses valores de cada elemento, considerando furos como elementos de área negativa:
Nessa tabela, a área do círculo foi obtida usando a fórmula e é negativa uma vez que o círculo se trata de um furo.
Por último, fazemos o somatório das áreas e dos produtos e colocamos esses resultados na última linha da tabela:
Com isso, podemos finalmente calcular a posição da linha neutra:
E assim, o item está resolvido!
Passo 3
Seguindo com o item ...
Começamos calculando o momento de inércia da área de cada elemento.
Para o elemento , retangular, temos:
Substituindo e , encontramos:
E para o elemento , que é um furo circular, temos:
Substituindo , encontramos:
Em seguida, temos que determinar as distâncias entre o centro de cada elemento e a linha neutra:
O centro do elemento está a uma altura de , então sua distância vai dar:
E o centro do elemento está a uma altura de , então a sua distância dá:
Com isso, podemos agora aplicar a fórmula abaixo para determinar o momento de inércia da área da seção transversal da viga:
Realizando esse somatório, temos:
Substituindo os valores:
- , e ;
- & , e ,
E calculando tudo, vamos encontrar que:
Que é a nossa resposta para o item .
Passo 4
No item , queremos calcular as tensões de tração () e compressão () máximas nessa viga devido à sua flexão.
Sabemos que essas tensões vão ser regidas pela fórmula da flexão:
E sabemos os valores de (do enunciado) e (do passo anterior).
Ou seja, só falta pensarmos nos valores máximos de para encontrarmos as tensões máximas.
Então vamos pensar...
Por um lado, temos que quando tiver seu valor negativo máximo, vai ter o seu valor positivo (de tração) máximo.
Esse valor negativo máximo de ocorre na base da viga, onde a posição dos pontos em relação à linha neutra vale:
Dessa forma, temos que:
Substituindo:
- ;
- ;
- & ,
Encontramos que:
não é uma unidade usual, então precisamos converter esse resultado para :
Por outro lado, quando tiver seu valor positivo máximo, vai ter o seu valor negativo (de compressão) máximo.
Essa valor positivo máximo de ocorre no topo da viga, onde a posição dos pontos em relação à linha neutra vale:
Dessa forma, temos que:
Substituindo:
- ;
- ;
- & ,
Encontramos que:
Realizando a conversão de para , multiplicamos esse valor por , obtendo:
Passo 5
Resolvido o item , agora só falta desenhar um gráfico para a distribuição de tensões em uma seção transversal da viga para o item .
Considerando um eixo começando na base da nossa viga, sabemos que:
- Na base da viga, onde , ocorre a tensão máxima de tração ;
- Na linha neutra, onde , a tensão é nula; (Isso sempre ocorre na linha neutra!)
- E no topo da viga, onde , ocorre a tensão máxima de compressão .
Marcando esses pontos em um gráfico e sabendo que a tensão varia linearmente com a variação de , ficamos com o gráfico abaixo:
E terminamos o exercício!
Resposta
Exercício Resolvido #3
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 212-6.73.
Determine o menor diâmetro admissível do eixo que está sujeita às forças concentradas. Os mancais de luva em e suportam somente forças verticais, e a tensão de flexão admissível é .
Passo 1
O que é que o exercício quer?
Ele quer saber qual é o menor diâmetro que o eixo circular pode ter de tal forma que a tensão de flexão no eixo não ultrapasse em módulo o seu valor admissível .
Ou seja, ele quer saber qual é o menor diâmetro que respeita a condição:
Então para resolver essa questão, precisamos saber descrever em função do diâmetro do eixo.
E como podemos fazer isso?
Bom, para descrever , precisamos avaliar os valores de de acordo com a fórmula da flexão:
Onde:
- (ou alternativamente, só “”) é o momento fletor em uma seção do eixo;
- é a posição de um ponto da seção do eixo em relação à sua linha neutra;
- & (ou alternativamente, só “”) é o momento de inércia da área da seção transversal desse eixo.
Mas olha só...
Primeiro, o momento fletor máximo absoluto “” nesse eixo pode ser encontrado a partir dos métodos da estática (DCL, equilíbrio, análise dos esforços internos & diagramas de esforços internos).
Segundo, a linha neutra de um eixo circular fica bem no meio do eixo, e, então, o valor máximo absoluto de vai corresponder ao raio do eixo:
E terceiro, o momento de inércia da área de uma seção transversal circular é:
Que ainda pode ser expressa em função do diâmetro do eixo como:
Então pode ser definido como:
O que simplificando, fica assim:
Então resumindo tudo...
Para resolver esse exercício, precisamos aplicar os métodos da estática para determinar o momento fletor máximo absoluto nesse eixo.
Feito isso, vamos conseguir descrever a tensão máxima absoluta no eixo em função do diâmetro .
E, em seguida, vamos poder usar isso e a condição de projeto para descobrirmos os diâmetro necessário para o nosso eixo.
Passo 2
Então vamos lá!
Começando pelo primeiro passo dos métodos da estática, nós temos o DCL ou:
O exercício já falou que os apoios em e só realizam reações na vertical, então nosso DCL fica assim:
Passo 3
Próximo passo é o:
Aplicando no nosso eixo o equilíbrio de forças na vertical, nós vamos ter que:
O que significa que:
Por outro lado, aplicando o equilíbrio de momentos em relação ao ponto , temos:
Isolando e calculando o restante, temos que:
O que significa que:
Por fim, substituindo esse valor na expressão anterior , encontramos que:
E assim finalizamos toda a análise dos esforços externos no nosso eixo!
Passo 4
Com isso, podemos seguir para o terceiro passo dos métodos da estática, que é a:
Existem descontinuidades (nesse caso, forças concentradas) nos pontos , , e da nossa viga.
Então devemos observar os esforços internos nas seções entre e , entre e e entre e :
Aí, como nesse exercício queremos analisar o momento fletor máximo absoluto no eixo, vamos focar em determinar os momentos fletores no eixo, pulando o cálculo das forças cortantes .
Para as seções as seções entre e , o equilíbrio de momentos em relação ao ponto da seção nos diz que:
O que significa que:
Em seguida, para as seções entre e , temos:
Substituindo e isolando , temos:
Fazendo a distributiva, isso fica assim:
O que significa que:
Por fim, para as seções entre e , temos:
Isolando , temos:
E fazendo a distributiva, encontramos que:
Passo 5
Finalmente, chegamos no último passo dos métodos da estática, que são os:
Aqui, só precisamos fazer um diagrama para o momento fletor da viga, que é descrito por 3 equações de primeiro grau de :
Pela primeira equação, o momento fletor varia linearmente de para .
Pela segunda, ele varia linearmente de para .
E pela terceira, ele varia linearmente de para .
Dessa forma, o diagrama do momento fletor fica assim:
E tcharam!
Desse diagrama conseguimos identifica que o momento fletor máximo absoluto no nosso eixo é:
Passo 6
Agora, podemos seguir o exercício aplicando a nossa condição:
Aplicando a fórmula da flexão para a determinação da tensão máxima absoluta no eixo, temos que:
De tal forma que a nossa condição pode ser reescrita assim:
Em seguida, substituindo:
- ;
- & ,
...e simplificando tudo, a nossa condição fica assim:
E isolando , temos:
Aí, substituindo os valores:
- ,
- & ,
...e não se esquecendo de fazer a raíz cúbica, encontramos que:
O que significa que o diâmetro mínimo necessário para o eixo é:
Resposta
Exercício Resolvido #4
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 245-4.9.
Duas forças verticais são aplicadas à viga com seção transversal mostrada na figura. Determine as tensões de tração e de compressão máximas na parte da viga.
Passo 1
O que está acontecendo?
Existe no trecho da viga um momento fletor (ou só “”) que pode ser encontrado através dos métodos da estática: diagrama de corpo livre, equilíbrio e análise dos esforços internos.
Além disso...
A seção transversal dessa viga tem uma linha neutra de posição e um momento de inércia da área (ou só “”) que podem ser determinados a partir da geometria da seção mostrada.
E o que é que o exercício quer?
Ele quer que a gente determine as tensões de tração e de compressão máximas devido à flexão no trecho da viga.
Essas tensões podem ser encontradas usando a fórmula da flexão:
...onde é a posição do ponto da seção que está sendo avaliado em relação à linha neutra.
Dessa forma, os valores máximos positivo e negativo de (e consequentemente os valores máximos de ) ocorrem para a base e para o topo da seção:
Então para resolver o exercício, devemos:
- Usar os métodos da estática para descobrir o valor de no trecho da viga;
- Encontrar os valores de e para a seção transversal da viga;
- E, finalmente, definir e e calcular as tensões de tração e de compressão máximas usando a fórmula da flexão.
Passo 2
Então vamos começar com o primeiro passo dos métodos da estática, que é o DCL ou:
Para essa viga:
- O apoio móvel em vai realizar uma reação na vertical ;
- E o apoio fixo em vai realizar uma reação na horizontal (que vai acabar sendo nula e pode ser omitida do DCL) e uma reação na vertical .
Dessa forma, o nosso DCL fica assim:
Passo 3
Agora, seguimos para o:
Aplicando o equilíbrio de forças na vertical, temos:
O que significa que:
Em seguida, aplicando o equilíbrio de momentos em relação ao ponto , temos:
Isolando , encontramos que:
O que significa que:
E, substituindo esse valor na expressão anterior , encontramos que:
Passo 4
Por fim, fazemos a:
Como nesse exercício, só queremos saber o momento fletor no trecho da viga, só precisamos analisar os esforços internos nas seções desse trecho:
Aí, para encontrar o valor do momento fletor nesse trecho, podemos aplicar o equilíbrio de momentos em relação ao ponto da seção:
Isolando , temos:
Substituindo e fazendo a distributiva, isso fica assim:
Finalmente, cortando com , encontramos que:
Passo 5
Agora, seguimos para a próxima parte do exercício, em que calculamos as propriedades geométricas da seção dessa viga, começando pela:
Para calcular essa posição, devemos observar a geometria da seção da viga:
Em seguida, separamos essa geometria em elementos numerados e definimos a base da viga como o ponto :
Calculamos as áreas de cada elemento e as posições dos centros de cada um e colocamos esses resultados em uma tabela:
Sendo que, nessa tabela, também colocamos na coluna final os produtos entre esses valores para cada elemento e na linha final os somatórios das áreas e dos produtos .
Com isso, podemos finalmente calcular a posição da linha neutra usando a fórmula:
Substituindo e , encontramos que:
Que é a posição da nossa linha neutra.
Passo 6
Depois da posição da linha neutra, podemos calcular para a seção da nossa viga o:
Começamos calculando o momento de inércia da área de cada elemento.
Todos os elementos que compõem a seção da nossa viga são retangulares.
Dessa forma, todos eles vão ter momentos de inércia da área .
Para os elementos e , que está “em pé” com uma base e uma altura , vamos ter que:
Já para o elemento , que está “deitado” com uma base e uma altura , temos:
Em seguida, temos que determinar as distâncias entre o centro de cada elemento e a linha neutra:
O centro dos elementos e estão a uma altura de , então:
Já o centro do elemento está a uma altura de , então a sua distância vai dar:
Com isso, podemos agora aplicar a fórmula abaixo, baseada no teorema dos eixos paralelos, para determinar o momento de inércia da área da seção transversal como um todo:
Realizando esse somatório, temos:
Substituindo os valores:
- e ;
- e ;
- & ,
E calculando tudo, vamos encontrar que:
Passo 7
Depois de tudo que passamos, chegamos ao passo final, que é definir e e calcular as tensões de tração e de compressão máximas no trecho da viga usando a fórmula da flexão.
Se lembrarmos do que vimos lá no passo 1:
Vamos poder definir agora os valores de e aproveitando o valor da posição da linha neutra que encontramos no passo 5:
Definidos esses valores, sabemos que:
Por um lado, o valor máximo negativo de , vai corresponder à tensão de flexão máxima de tração () no trecho da viga:
Substituindo:
- Do passo , ;
- Do passo , ;
- E do passo atual, ,
- Do passo , ;
- Do passo , ;
- E do passo atual, ,
Vamos encontrar que:
E, como é o mesmo que , isso significa que:
Por outro lado, o valor máximo positivo de , vai corresponder à tensão de flexão máxima de compressão () no trecho da viga:
Daí que, substituindo:
E calculando tudo, encontramos que:
E assim, terminamos o exercício!
Resposta
Exercício Resolvido #5
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 339-5.22.
Trace os diagramas de força cortante e momento fletor para a viga e carregamento mostrados na figura, e determine a tensão normal máxima provocada pelo momento fletor.
Dados: Um perfil possui uma seção transversal simétrica na horizontal e na vertical, com altura de e momento de inércia da área .
Passo 1
O que está acontecendo?
O carregamento nessa viga vai produzir ao longo dele esforços internos na forma de forças cortantes e momentos fletores .
Daí que, em uma certa seção dessa viga, o momento fletor vai possuir o seu valor máximo em termos absolutos.
Nessa seção, ocorrerá a tensão normal de flexão máxima nessa viga, de acordo com a fórmula da flexão:
Onde:
- (ou só “”) é o momento fletor em uma seção transversal da viga;
- é a posição do ponto da seção em que se quer calcular a tensão em relação à linha neutra da seção;
- & (ou só “”) é o momento de inércia da área da seção.
Além disso...
A viga foi feita com um perfil padronizado “”, de altura e momento de inércia da área .
Esse perfil, por ser simétrico, ainda tem uma linha neutra que passa bem no meio dele:
Dessa forma, as posições em relação à linha neutra de valores críticos (máximos) nesse perfil vão ser para o topo da seção e para a base.
E o que é que o exercício quer?
Primeiro, ele quer que a gente faça os diagramas de força cortante e momento fletor para essa viga.
Para tanto, podemos recorrer aos métodos da estática: DCL, equilíbrio, análise dos esforços internos & diagramas de esforços internos.
Em seguida, ele quer que a gente determine a tensão normal de flexão máxima nessa viga.
Para tanto, podemos aplicar a fórmula da flexão utilizando os valores máximos/críticos encontrados anteriormente para e .
Passo 2
Então vamos começar com o primeiro passo dos métodos da estática, que é o DCL ou:
Para essa viga:
- O apoio fixo em vai realizar uma reação na horizontal (que vai acabar sendo nula e pode ser omitida do DCL) e uma reação na vertical .
- E o apoio móvel em vai realizar uma reação na vertical ;
Dessa forma, o nosso DCL vai ficar assim:
Passo 3
Feito o DCL, seguimos para o:
Aplicando o equilíbrio de forças na vertical, vamos ter:
Na hora de fazer esse somatório, consideramos a força distribuída uniforme de que atua ao longo do comprimento de da viga como uma força equivalente:
Dessa forma, o nosso somatório de forças na vertical fica assim:
O que significa que:
Em seguida, podemos aplicar o equilíbrio de momentos em relação ao ponto :
Aqui, como a força distribuída de é uniforme, podemos considerar que a sua força equivalente de atua bem no meio do comprimento de .
Dessa forma, temos que o braço da força equivalente de em relação ao ponto vai ser .
Sabendo disso e considerando os momentos no sentido anti-horário como positivo (), o nosso somatório de momentos fica assim:
Isolando , temos:
Calculando tudo, encontramos que:
Em seguida, substituindo isso na expressão anterior , encontramos que:
Passo 4
Encontrados os valores dos esforços externos atuantes na nossa viga, podemos seguir agora para a:
Na nossa viga, temos descontinuidades:
- em ; (início da viga, início de uma força distribuída, força concentrada e momento concentrado)
- em ; (fim de uma força distribuída)
- & em . (final da viga, força concentrada e momento concentrado)
Então precisamos avaliar as seções entre e & as seções entre e :
Feitos os desenhos acima, precisamos aplicar as condições de equilíbrio em cada situação para conseguirmos descrever os esforços internos e na viga.
Primeiro, analisamos as seções entre e .
Aplicando o equilíbrio de forças na vertical, temos:
Aqui, a força distribuída uniforme de que atua ao longo do comprimento pode ser considerada como uma força equivalente .
Dessa forma, o nosso somatório de forças fica assim:
Substituindo e isolando , encontramos que:
Em seguida, aplicando o equilíbrio de momentos em relação ao ponto da seção, temos:
Aqui, como a força distribuída de é uniforme, podemos considerar que a sua força equivalente de atua bem no meio do pedaço de viga que estamos estudando.
Sendo assim, o nosso somatório de momentos fica assim:
Substituindo e isolando , encontramos que:
Depois, analisamos as seções entre e :
Aplicando o equilíbrio de forças na vertical, temos que:
Isolando e substituindo , encontramos que:
Em seguida, aplicando o equilíbrio de momentos em relação ao ponto da seção, temos:
Considerando que os momentos no sentido anti-horário são positivos (), esse somatório fica assim:
Isolando e substituindo , temos que:
Fazendo a distributiva e arrumando tudo, encontramos que:
Passo 5
Por fim, podemos seguir para o último passo dos métodos da estática, que são os:
Para a força cortante , temos:
- Que ela segue a equação quando , variando linearmente entre os pontos e ;
- E que ele é igual quando .
Dessa forma, o diagrama da força cortante fica assim:
Quanto ao momento fletor , ele é descrito por duas equações:
Primeiro, para , ele é descrito pela função quadrática:
O que significa que ele varia parabolicamente, com uma concavidade para baixo (uma vez que a segunda derivada dessa função acima é negativa), entre os pontos:
Além disso...
Fazendo a primeira derivada dessa função e igualando-a a zero, encontramos que o ponto crítico dessa função é .
E, como a função tem uma concavidade para baixo, esse ponto crítico vai ser o seu ponto de máximo.
Calculando o valor de para esse ponto, temos:
Em seguida, para o trecho , temos uma função de primeiro grau:
Dessa forma, temos que nesse trecho, o momento fletor varia linearmente entre os pontos:
Tendo tudo o que vimos em mente, conseguimos desenhar o diagrama de momento fletor para essa viga, que fica assim:
Aí, desse diagrama acima, conseguimos identificar que o momento fletor máximos em termos absolutos nessa viga é:
E assim terminamos toda a parte dos métodos da estática!
Passo 6
Agora, como o exercício já nos forneceu as propriedades geométricas da seção transversal dessa viga, podemos seguir direto para o cálculo da tensão normal de flexão máxima na viga.
Para tanto, podemos aplicar a fórmula da flexão:
Substituindo nessa fórmula:
- O momento fletor máximo na viga ;
- Os valores críticos de , ;
- E o valor de , ,
Vamos encontrar as tensões máximas de tração e de compressão na nossa viga:
Simplificando, isso fica assim:
Calculando tudo e sabendo que é o mesmo que , encontramos que as tensões máximas de tração e compressão nessa viga são:
Sendo que o valor negativo, de compressão, ocorre no topo da viga, onde , e o valor positivo, de tração, ocorre na base da viga, onde .
Finalmente, na hora de darmos o resultado final do exercício, podemos indicar só o valor absoluto desse resultado:
Resposta
Exercício Resolvido #6
Prova 1 - 2017.1 - Prof. Alex - Mecânica dos Materiais 1 - UnB (Adaptada)
A viga da figura abaixo possui um comprimento total , está submetida a uma carga uniformemente distribuída e possui uma seção transversal na forma de um tubo quadrado, com lados externos de comprimento e lados internos de comprimento .
Determine a tensão de flexão máxima nessa viga e faça um rascunho da distribuição de tensões na seção transversal da viga onde ocorre essa tensão máxima.
Passo 1
O que está acontecendo?
A carga distribuída uniformemente e as reações realizadas pelos apoios nessa viga vão gerar nela esforços internos na forma de forças cortantes e momentos fletores .
Em uma ou mais seções transversais dessa viga, o momento fletor vai ter o seu valor máximo absoluto.
Nessas seções de momento máximo, vão ocorrer as tensões de flexão máximas na viga, de acordo com a fórmula da flexão:
Onde:
- (ou só “” para alguns professores) é o momento fletor na seção transversal;
- é a posição do ponto da seção transversal em que se quer avaliar a tensão em relação à linha neutra da seção;
- & (ou só “” para alguns professores) é o momento de inércia da área da seção.
E o que é que o exercício quer?
Ele quer que a gente determine a maior tensão de flexão causada nessa viga em função das variáveis , , e que ele indicou no enunciado.
Então...
Para resolver esse exercício, temos que:
1. Encontrar o momento fletor máximo em termos absolutos nessa viga.
Para tanto, devemos usar os métodos da estática: DCL, equilíbrio, análise dos esforços internos & diagramas de esforços internos.
2. Analisar a geometria da seção transversal dessa viga para encontrar a posição de sua linha neutra e o seu momento de inércia da área .
Aqui, como a seção dessa viga é simétrica em relação à horizontal, já podemos afirmar que a sua linha neutra possui uma posição média :
Além disso, também vemos que os maiores valores da posição de um ponto dessa seção transversal em relação à linha neutra são para o topo da seção e para a base.
Dessa forma, só falta calcular para essa seção o momento de inércia da área .
& 3. Aplicar a fórmula da flexão para os valores máximos absolutos de e , encontrando assim a tensão de flexão máxima nessa viga, resolvendo o exercício.
Ao final, o exercício ainda pede que a gente aproveite os resultados obtidos para fazer um rascunho da distribuição de tensões na seção transversal da viga onde ocorre essa tensão máxima.
Passo 2
Então vamos começar pelo primeiro passo dos métodos da estática, que é o DCL ou:
Para essa viga:
- O apoio móvel à direita vai realizar uma reação na vertical ;
- E o apoio fixo na extremidade esquerda vai realizar uma reação na horizontal (que vai acabar sendo nula e pode ser omitida do DCL) e uma reação na vertical .
Dessa forma, o nosso DCL fica assim:
Passo 3
Feito o DCL, seguimos para o:
Aplicando o equilíbrio de forças na vertical, temos:
Na hora de fazer esse somatório, consideramos a força uniformemente distribuída que atua ao longo do comprimento total da viga como uma força equivalente .
Dessa forma, o somatório fica assim:
O que significa que:
Em seguida, podemos aplicar o equilíbrio de momentos em relação ao ponto da viga:
Aqui, como a força distribuída é uniforme, nós temos que a sua força equivalente atua bem no meio da viga.
Dessa forma, a força equivalente vai ter um braço em relação ao ponto .
Sabendo disso, podemos fazer o somatório de momentos acima, que fica assim:
Isolando , temos que:
Cortando com e depois isolando , encontramos que:
Por fim, podemos substituir esse valor na expressão anterior e isolar para encontrar que:
Passo 4
Agora, já conhecemos os valores dos esforços externos atuantes na nossa viga.
Então podemos seguir agora para a:
Nessa viga, temos descontinuidades em , e , então precisamos avaliar as seções entre e e as seções entre e :
Aí, para finalizar a análise dos esforços internos, devemos aplicar as equações de equilíbrio em cada situação para descobrirmos os valores dos esforços internos e nas diferentes seções da viga.
Mas no caso desse exercício...
Ele só quer descobrir as tensões de flexão máximas, que são causadas pelo momento fletor .
Então só precisamos aplicar o equilíbrio de momentos em relação ao ponto da seção em cada situação para descobrirmos os valores de .
Para as seções entre e , vamos ter:
Olhando para o desenho acima do pedaço de viga para as seções entre e , vemos que a força uniformemente distribuída atua ao longo do comprimento desse pedaço de viga.
Assim, concluímos que ela vai atuar como uma força equivalente com um braço em relação ao ponto da seção.
Percebendo como nesse caso, somente o momento gerado pela força vai estar no sentido horário (), o nosso somatório de momentos fica assim:
Substituindo , temos:
Em seguida, isolando , encontramos que:
Já para as seções entre e , temos:
Dessa vez, a força distribuída vai atuar como uma força equivalente com um braço em relação ao ponto da seção.
Percebendo como, nesse caso, tanto o momento fletor quando o momento gerado por estão no sentido horário (), o nosso somatório de momentos fica assim:
Isolando , encontramos que:
Desenvolvendo o termo , temos:
Finalmente, fazendo a distributiva, conseguimos indicar a função que expressa o momento fletor nas seções entre e em função da posição que está sendo avaliada:
Passo 5
Por fim, podemos seguir para o último passo dos métodos da estática, que são os:
No passo anterior, vimos que o momento fletor é descrito por duas funções.
Primeiro, vimos que para o trecho , o momento fletor é dado por:
Analisando essa função, podemos observar que:
- A sua segunda derivada é negativa. Assim podemos concluir que essa função quadrática possui uma concavidade virada para baixo.
- O seu ponto crítico (aquele em que a sua primeira derivada é igual à zero) ocorre em .
- E que, como ela possui uma concavidade para baixo, esse ponto crítico é um ponto de máximo para a função.
Além disso, podemos calcular o valor do momento fletor no ponto :
No ponto de máximo :
E no ponto :
Em seguida, para o trecho , o momento fletor é dado por:
Analisando essa função, observamos:
- Que ela possui uma concavidade para baixo, uma vez que a sua segunda derivada é negativa;
- Que o seu ponto crítico (aquele em que a sua primeira derivada é igual à zero) ocorre em ;
- E que, como essa função possui uma concavidade para baixo, esse ponto crítico é um ponto de máximo.
Além disso, podemos calcular o momento fletor no ponto :
O que vai dar:
E podemos calcular o momento fletor no ponto de máximo :
Que vai dar:
Assim...
Usando todos esses pontos e conhecendo a concavidade dessas curvas, conseguimos desenhar o diagrama de momento fletor para essa viga:
E, desse diagrama de momento fletor, conseguimos retirar que o momento fletor máximo nessa viga em termos absolutos é:
Além disso...
Para resolver esse exercício, não é necessário fazer o diagrama da força cortante na viga.
Mas mesmo assim, muitos professores pedem que esse diagrama seja sempre feito.
Então, caso você queira fazer esse diagrama em casa e comparar os resultados, ele fica assim:
Passo 6
Agora, vamos estudar as propriedades geométricas da seção transversal dessa viga.
No passo 1, nós já vimos que a posição da linha neutra da seção transversal dessa viga é , uma vez que a seção transversal é simétrica em relação à horizontal.
Então só nos resta calcular o:
Para calcular o momento de inércia da área da seção transversal dessa viga, devemos observar a sua geometria:
Em seguida, devemos separar essa geometria em elementos numerados.
Aqui, nós temos duas opções:
A primeira opção é separar a geometria da seção em 4 retângulos numerados:
Mas essa opção vai resultar em cálculos desnecessariamente complicados.
Já a segunda opção é separar a geometria em um quadrado maior de lado (elemento na figura abaixo) e um furo na forma de uma quadrado menor de lado (elemento na figura):
Sendo que, nessa segunda opção, precisamos considerar o elemento que é um furo como um elemento de momento de inércia da área negativo e de área negativa.
A segunda opção facilita os cálculos, então vamos escolher ela!
Definidos os elementos que compõem a geometria da nossa seção, devemos calcular em seguida o momento de inércia da área de cada elemento.
No nosso caso, tanto o elemento quanto o elemento são quadrados.
Dessa forma, podemos usar para eles a fórmula do momento de inércia da área de um retângulo:
Para o elemento , um quadrado de lado , nós vamos ter uma base e uma altura , de tal forma que:
Já para o elemento , um quadrado de lado , vamos ter uma base e uma altura .
Lembrando que o elemento é um furo e, portanto, deve ter um valor de negativo, o seu momento de inércia da área fica assim:
Em seguida, como os elementos e da nossa seção já estão centrados na linha neutra da seção, não precisamos usar o teorema dos eixos paralelos.
Assim, o momento de inércia da área da seção transversal como um todo vai ser dado pela soma:
Substituindo os valores de e , vamos ter:
O que significa que:
Passo 7
Finalmente, podemos calcular a tensão de flexão máxima na nossa viga.
Aplicando a fórmula de flexão, temos:
Aí, sabendo que a tensão máxima na viga vai ocorrer:
- Na seção em que o momento fletor tem seu valor máximo em termos absolutos ;
- E nos pontos em que tem seus valores máximos em termos absolutos, que são no topo da seção da viga, onde , e na base da seção, onde ,
E substituindo , encontramos que as tensões máximas na nossa viga vão ser:
Simplificando essa expressão, temos:
E, como , isso significa que:
Sendo que o valor positivo, de tração, ocorre o no topo da seção da viga, onde , e o valor negativo, de compressão, ocorre na base, onde .
(Isso porque o nosso momento fletor é negativo. Caso ele fosse positivo, o contrário ocorreria!)
Aí, para fornecer a nossa resposta final, podemos indicar somente o valor absoluto:
E assim encontramos a nossa resposta para o exercício!
Passo 8
Por último, o exercício ainda quer que a gente faça um rascunho da distribuição de tensões na seção onde ocorre essa tensão .
Então vamos pensar...
Definindo uma coordenada começando na base da seção da viga:
...vamos ter que:
- Na base da seção, na posição , a tensão vai ser igual a , como acabamos de ver no passo anterior;
- No topo da seção, de posição , ela vai ser igual a , também como acabamos de ver;
- E no centro da seção, de posição , onde há a linha neutra de tal forma que a posição da fórmula da flexão vai ser nula, a tensão vai ser nula.
Aí, marcando esses pontos em um gráfico, e ligando eles por uma reta, vamos ter o nosso rascunho da distribuição de tensões na seção:
E assim terminamos de vez o exercício!
Resposta
Exercício Resolvido #7
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 351-5.62.
A viga suporta uma força uniformemente distribuída de e duas forças concentradas e . Foi determinado experimentalmente que a tensão normal provocada pelo momento fletor na borda inferior da viga fosse de em e de em . Trace os diagramas de força cortante e momento fletor para a viga, e determine a intensidade das forças e .
Passo 1
O que está acontecendo?
Devido ao carregamento nessa viga, existem ao longo dela esforços internos na forma de forças cortantes e momentos fletores .
Devido a esses momentos fletores , surgem ao longo da viga tensões normais de tração () e compressão () de acordo com a fórmula da flexão:
Onde:
- (ou só “”) é o momento fletor em uma seção transversal da viga;
- é a posição do ponto da seção em que se quer calcular a tensão em relação à linha neutra da seção;
- & (ou só “”) é o momento de inércia da área da seção.
Aí...
O exercício nos diz que na borda inferior da viga, nos pontos em que a posição em relação à linha neutra :
...a tensão na seção é:
...enquanto que a tensão na seção é:
Sendo que como a seção transversal dessa viga é simétrica, a sua linha neutra fica bem no meio da seção:
O que significa que a posição em relação à linha neutra dos pontos da borda inferior é:
E além disso, o momento de inércia da área dessa seção transversal retangular de base e altura pode ser calculado pela fórmula:
O que tudo isso significa é que...
Aplicando a fórmula da flexão para a borda inferior das seções e , vamos conseguir descobrir o valor do momento fletor nessas seções.
E o que é que o exercício quer?
Ele quer saber o valor das forças e desconhecidas na viga.
Então, o que a gente pode fazer é:
1. Utilizar os métodos da estática (DCL, equilíbrio e análise dos esforços internos) para descobrir o valor do momento fletor nas seções e da viga em função das forças e .
2. Aplicar a fórmula da flexão para a borda inferior das seções e para encontrar o valor do momento fletor nas seções e .
& 3. Igualar os resultados para o momento fletor em e obtidos pelo primeiro e pelo segundo método para podermos isolar e encontrar os valores das forças e .
Ao final, o exercício ainda pede que a gente faça os diagramas de força cortante e de momento fletor para essa viga.
Passo 2
Então vamos começar com o primeiro passo dos métodos da estática, que é o DCL ou:
Para essa viga, o engaste em vai realizar:
- Uma reação na horizontal, ; (que vai acabar sendo nula e pode ser omitida do DCL)
- Uma reação na vertical, ;
- E um momento .
Dessa forma, o nosso DCL vai ficar assim:
Passo 3
Feito o DCL, seguimos para o:
Aplicando o equilíbrio de forças na vertical, vamos ter:
Na hora de fazer esse somatório, consideramos a força distribuída uniforme de que atua ao longo do comprimento de da viga como uma força equivalente:
Dessa forma, o nosso somatório de forças na vertical fica assim:
O que significa que:
Sendo que esse resultado está em .
Em seguida, podemos aplicar o equilíbrio de momentos em relação ao ponto :
Aqui, como a força distribuída de é uniforme, podemos considerar que a sua força equivalente de atua no ponto , bem no meio do comprimento .
Sabendo disso e considerando os momentos no sentido anti-horário como positivo (), o nosso somatório de momentos fica assim:
Isolando , encontramos que:
Sendo que esse resultado está em .
Passo 4
Encontrados os valores dos esforços externos atuantes na nossa viga, seguimos para a:
Nessa viga, temos descontinuidades:
- em ; (início da viga, início de uma força distribuída, força concentrada e momento concentrado)
- em ; (fim de uma força distribuída e força concentrada)
- & em . (final da viga e força concentrada)
Então precisamos avaliar as seções entre e & as seções entre e :
Feitos esses desenhos, precisamos aplicar as condições de equilíbrio em cada caso.
Primeiro, observamos as seções entre e .
Aplicando o equilíbrio de forças na vertical, temos:
Aqui, a força distribuída uniforme de que atua ao longo do comprimento pode ser considerada como uma força equivalente .
Dessa forma, o nosso somatório de forças fica assim:
Substituindo e isolando , encontramos que:
Sendo que esse resultado está em !
Em seguida, aplicando o equilíbrio de momentos em relação ao ponto da seção, temos:
Aqui, como a força distribuída de é uniforme, podemos considerar que a sua força equivalente de atua bem no meio do pedaço de viga que estamos estudando.
Sendo assim, o nosso somatório de momentos fica assim:
Substituindo e , temos:
Isolando , encontramos que:
Sendo que esse resultado está em !
Em seguida, observamos as seções entre e .
Aplicando o equilíbrio de forças na vertical, temos que:
O que significa que:
Já aplicando o equilíbrio de momentos em relação ao ponto da seção, temos:
Fazendo a distributiva, temos:
Por fim, isolando , encontramos que:
Sendo que esse resultado está em !
E assim finalizamos a nossa análise dos esforços internos!
Passo 5
Agora, já podemos determinar quais são os momentos fletores nas seções e da viga em função das forças e .
Tanto a seção quanto a seção estão entre e .
Dessa forma, os momentos fletores nessas seções vão ser descritos pela fórmula:
Para a seção , temos que , de tal forma que:
Já para a seção , temos que , de tal forma que:
Desenvolvendo essa expressão, temos:
E, simplificando isso, encontramos que:
Lembrando que esses resultados para o momento fletor estão em !
Passo 6
Em seguida, precisamos encontrar os momentos fletores pelo segundo método, que é aplicando a fórmula da flexão para as bordas inferiores das seções e .
Aplicando a fórmula da flexão, temos:
Primeiramente, para a borda inferior da seção , vamos substituir:
- ;
- ;
- ;
- & ,
- ;
- ;
- ;
- & ,
De tal forma que:
Isolando , temos que:
Simplificando isso, encontramos:
O que dá:
Agora, como o resultado que encontramos para pelos métodos da estática estão em , vamos converter esse resultado também para , obtendo que:
Depois, para a borda inferior da seção , substituímos:
De tal forma que:
Isolando e simplificando tudo, encontramos que:
O que dá:
Passo 7
Determinados os valores de e pelos dois métodos e estando tudo em , podemos igualar agora esses valores.
Primeiro, para , temos:
Isolando , encontramos que:
Já para , temos:
Substituindo , isso fica assim:
Fazendo a distributiva:
Simplificando:
Isolando , encontramos que:
Inserindo esse resultado em , temos:
Ou seja, temos que:
Passo 8
Aqui, praticamente já resolvemos o exercício: só falta fazermos os:
Para a força cortante , temos que:
Primeiro, ela é descrita pela equação no trecho .
Substituindo e , essa equação fica assim:
O que significa que a força cortante varia linearmente entre os pontos e .
Depois, ela é dada por no trecho .
Dessa forma, o diagrama da força cortante fica assim:
Já para o momento fletor , temos que:
Primeiro, ele é descrito por:
...no trecho .
Substituindo e , essa equação fica assim:
O que significa que o momento fletor varia parabolicamente, com uma concavidade para baixo (uma vez que a segunda derivada da função acima é negativa), entre os pontos:
Além disso, fazendo a primeira derivada dessa função e igualando-a a zero, encontramos que o seu ponto crítico é , o que está fora do trecho .
Em seguida, ele é descrito por:
...no trecho .
Substituindo , isso fica assim:
O que significa que varia linearmente entre os pontos:
Dessa forma, o nosso diagrama de momento fletor fica assim:
E assim terminamos o nosso exercício!
Resposta
Exercício Resolvido #8
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 360-5.85.
Determine o maior valor admissível da carga distribuída para a viga mostrada, sabendo que a tensão normal admissível é de em tração e de em compressão.
Passo 1
O que nós sabemos?
Sabemos que o carregamento na viga vai gerar nela esforços internos na forma de forças cortantes e momentos fletores .
Esses momentos fletores vão gerar na viga tensões normais de flexão , de acordo com a fórmula da flexão:
Onde:
- (ou só “”) é o momento fletor em uma seção transversal da viga;
- é a posição do ponto da seção em que se quer calcular a tensão em relação à linha neutra da seção;
- & (ou só “”) é o momento de inércia da área da seção.
Lembrando que nessa equação, dependendo dos sinais de e de , a tensão pode assumir valores positivos (de tração) ou negativos (de compressão).
Beleza...
E o que é que está acontecendo no exercício?
Nesse exercício, vamos ter certas seções da viga onde o momento fletor vai ter os seus “valores críticos”: os seus maiores valores positivo e negativo.
Nessas seções, que vamos chamar de “seções críticas”, há a chance de que a tensão normal atinja, ou no topo ou na base da seção, o seu valor máximo em tração ():
...e/ou o seu valor máximo em compressão ():
...sendo que, para a viga do exercício, essas tensões tem que ser monitoradas para garantir que elas não ultrapassem os seus valores máximos admissíveis de e .
Ou seja, essas tensões tem que satisfazer as condições:
E o que é que o exercício quer?
Ele quer que a gente determine o valor máximo da carga distribuída de tal forma que as condições acima ainda sejam respeitadas.
Então, para resolver esse exercício, vamos ter que:
1. Encontrar os momentos fletores críticos na viga em função de .
Para tanto, podemos aplicar os métodos da estática: DCL, equilíbrio, análise dos esforços internos & diagramas de esforços internos.
2. Analisar a geometria em “T” da seção transversal da viga para encontrar a posição de sua linha neutra e o seu momento de inércia da área .
3. Definir os “valores críticos” de para a viga e aplicar a fórmula da flexão usando esses valores e os momentos fletores críticos encontrados anteriormente.
Assim, vamos encontrar as tensões máximas de tração () e compressão () na viga em função da carga distribuída desconhecida .
E, finalmente, 4. Aplicar as condições e .
Assim, vamos descobrir os valores máximos permitidos para de acordo com essas condições, resolvendo então o exercício.
Passo 2
Então vamos começar encontrando os momentos fletores críticos na viga através dos métodos da estática!
Começando pelo primeiro passo dos métodos da estática, temos o DCL ou:
Para essa viga:
- O apoio móvel em vai realizar uma reação na vertical ;
- E o apoio fixo em vai realizar uma reação na horizontal (que vai acabar sendo nula e pode ser omitida do DCL) e uma reação na vertical .
Então o DCL dessa viga deve ficar assim:
Passo 3
Feito o DCL, seguimos para o:
Aplicando o equilíbrio de forças na vertical, vamos ter:
Na hora de fazer esse somatório, consideramos a força distribuída uniforme que atua ao longo do comprimento total de da viga como uma força equivalente .
Dessa forma, o somatório fica assim:
O que significa que:
Em seguida, podemos aplicar o equilíbrio de momentos em relação ao ponto médio “” da viga, onde a força equivalente à força distribuída uniforme atua:
Dessa forma, vamos ter:
O que significa que:
Daí que, substituindo isso na expressão anterior , conseguimos encontrar que:
Passo 4
Encontrados os valores dos esforços externos atuantes na nossa viga, podemos seguir agora para a:
Na nossa viga, temos descontinuidades em (início da viga e de uma força distribuída), em e em (forças concentradas) e em (final da viga e de uma força distribuída).
Então precisamos avaliar as seções entre e , entre e e entre e :
Em cada caso, só queremos saber o valor do momento fletor , então podemos aplicar somente o equilíbrio de momentos em relação ao ponto da seção.
Além disso, em cada caso, podemos considerar a força distribuída como uma força equivalente que atua bem no meio da seção da viga em que se está aplicando o equilíbrio.
Para as seções entre e , vamos ter:
Lembrando que aqui, corresponde à força equivalente à carga distribuída enquanto corresponde ao seu braço.
Aí, isolando , encontramos que:
Em seguida, para as seções entre e , temos:
Isolando e fazendo a distributiva em “”, temos:
E finalmente, substituindo , encontramos que:
Por fim, para as seções entre e , temos:
Lembrando que nesse caso, corresponde à força equivalente à carga distribuída enquanto que é o seu bra��o.
Aí, isolando , encontramos que:
E, desenvolvendo essa expressão, encontramos:
O que significa que:
Passo 5
Por fim, podemos seguir para o último passo dos métodos da estática, que são os:
Sendo que aqui, importa para a gente fazer o diagrama do momento fletor .
Então vamos pensar...
Como vimos no passo anterior, o momento fletor é descrito por três equações, dependendo do trecho da viga que estamos analisando.
Primeiro, para o trecho , nós temos a função quadrática:
O que significa que o momento fletor varia parabolicamente, com uma concavidade para baixo (uma vez que a segunda derivada dessa função acima é negativa), entre os pontos:
Além disso...
Fazendo a primeira derivada dessa função e igualando-a a zero, encontramos que o ponto crítico dessa função é , onde , que vai ser o ponto de máximo da função, uma vez que ela tem uma concavidade para baixo.
Em seguida, para o trecho , temos outra função quadrática:
O que significa que o momento varia parabolicamente, com uma concavidade para baixo (pelo mesmo motivo da função anterior), entre os pontos:
Além disso...
Fazendo a primeira derivada dessa função e igualando-a a zero, encontramos o ponto de máximo , onde o momento fletor vai valer:
Por fim, para o trecho , temos uma terceira função quadrática:
O que significa que o momento varia parabolicamente, com uma concavidade para baixo (pelo mesmo motivo das funções anteriores), entre os pontos:
Além disso...
Fazendo a primeira derivada dessa função e igualando-a a zero, encontramos o ponto de máximo , o acabamos de calcular que o momento fletor é igual à zero.
Assim...
Juntando tudo que acabamos de ver...
Conseguimos desenhar o diagrama de momento fletor abaixo para essa viga:
E tcharam! 😎
Desse diagrama de momento fletor, conseguimos retirar que os valores críticos (os valores máximos positivo e negativo) do momento fletor nessa viga são:
E assim terminamos toda a parte dos métodos da estática.
Passo 6
Agora, podemos seguir para o estudo das propriedades geométricas da seção transversal dessa viga, começando pela determinação da:
Para calcular essa posição, devemos observar a geometria da seção da viga:
Em seguida, separamos essa geometria em elementos numerados e definimos a base da viga como o ponto :
Calculamos as áreas de cada elemento e as posições dos centros de cada um e colocamos esses resultados em uma tabela:
Sendo que, nessa tabela, também colocamos na coluna final os produtos entre esses valores para cada elemento e na linha final os somatórios das áreas e dos produtos .
Com isso, podemos finalmente calcular a posição da linha neutra usando a fórmula:
Substituindo e , encontramos que:
Que é a posição da nossa linha neutra!
Passo 7
Depois da posição da linha neutra, podemos calcular para a seção da nossa viga o:
Aqui, devemos começar calculando o momento de inércia da área de cada elemento.
No nosso caso, tanto o elemento quanto o elemento que compõem essa viga são retangulares.
Dessa forma, os dois vão ter momentos de inércia da área dados pela fórmula .
Assim, para o elemento , que está “deitado” com uma base e uma altura , vamos ter que:
Já para o elemento , que está “em pé” com uma base e uma altura , vamos ter que:
Em seguida, temos que determinar as distâncias entre o centro de cada elemento e a linha neutra:
Da tabela do passo 6, vemos que o centro do elemento está a uma altura de , então:
Já o centro do elemento está a uma altura de , então a sua distância vai dar:
Com isso, podemos agora aplicar a fórmula abaixo, baseada no teorema dos eixos paralelos, para determinar o momento de inércia da área da seção transversal como um todo:
Realizando esse somatório, temos:
Substituindo os valores:
- e ;
- e ;
- & ,
E calculando tudo, vamos encontrar que:
Passo 8
Agora, podemos definir os “valores críticos” (máximos positivo e negativo) de para essa viga.
Assim, vamos poder aplicar a fórmula da flexão usando esses valores e os valores críticos de encontrados lá no passo .
E, com isso, vamos encontrar as tensões máximas de tração () e compressão () na viga em função da carga distribuída desconhecida .
Então vamos lá!
Em qualquer viga, os valores máximos positivo e negativo de vão acontecer para o topo e para a base da viga.
Para a nossa viga:
- Já definimos a sua base como o ponto ;
- Já encontramos a posição da sua linha neutra;
- E, somando com , vemos que o seu topo vai ter uma altura de ,
...como mostra a figura abaixo:
Isso significa que o valor máximo positivo da posição de um ponto dessa seção em relação à sua linha neutra vai ser:
E que o valor máximo negativo da posição de um ponto dessa seção em relação à sua linha neutra vai ser:
Passo 9
Com esses valores, podemos calcular as tensões de tração e compressão máximas para os pontos críticos e (onde ) e (onde ).
Para os pontos e , temos:
Substituindo:
- para os pontos e ;
- e ;
- ,
- ;
- e ;
- ,
Encontramos que:
Já para o ponto , temos:
Substituindo, para o ponto :
Encontramos que:
Passo 10
Finalmente, com os resultados do passo passado, conseguimos ver que a tensão máxima de tração nessa viga é:
E que a tensão máxima de compressão na viga é:
Agora, podemos inserir esses valores nas nossas condições de projeto:
...que vão ficar assim:
Daí, sabendo que é o mesmo que e isolando nessas expressão acima, encontramos que:
Ou seja...
O valor máximo admissível para a carga distribuída é , ou , que é a nossa resposta!!!!
Resposta
Exercício Resolvido #9
Elaboração própria
a viga abaixo está sujeita ao carregamento mostrado. Sabendo que essa viga possui , determine o máximo valor da carga P que podemos aplicar sem que haja rompimento da viga. Considere apenas a contribuição de esforços fletores.
Passo 1
Como se trata de uma questão em que só consideraremos a contribuição dos esforços normais, e também temos uma resistência a tensão Normal, sabemos que a fórmula que devemos usar é a fórmula da flexão que é dada por
Mas podemos considerar algumas suposições, por exemplo, como queremos definir um valor máximo de carga, podemos fazer esse cálculo pelo módulo, ou seja, podemos retirar o sinal da nossa fórmula
Outra coisa que sabemos é que devemos usar a igualdade
Pois assim conseguiremos determinar o valor máximo que a peça aguenta sem romper.
Por fim, uma coisa que também temos que fazer é determinar o momento máximo que ocorre na nossa peça em função da nossa carga. Devemos usar o momento máximo pois queremos o ponto em que a viga será mais solicitada. Se ela suportar os esforços nesse ponto, aguentará em qualquer ponto.
Passo 2
Como a nossa viga está engastada, e todos os carregamentos estão na mesma direção, o maior momento que a nossa viga estará sujeita ocorrerá na parede, ou seja, no ponto A.
Para determinarmos o valor desse momento devemos desenhar o nosso diagrama de corpo livre
Com o nosso diagrama de corpo livre devemos fazer o equilíbrio da nossa peça para podermos calcular as reações de apoio
Podemos então isolar o valor de , e dessa forma teremos que
Agora que já determinamos o valor da reação vertical, vamos calcular o momento em A
E esse momento que calculamos é o nosso momento máximo
Passo 3
Agora que já temos o valor do nosso momento, precisamos definir os outros dois valores da nossa fórmula, que são os valores do momento de inercia e do y.
Vamos primeiro definir o nosso momento de inércia. Como a nossa seção é quadrada, sabemos que o momento de inércia é dado por
Como é uma seção quadrada, sabemos que
Substituindo na nossa fórmula teremos que
Como já dissemos antes também precisamos do valor de y, com isso teremos que
Como queremos sempre o valor máximo, sempre usaremos o valor mais distante da linha neutra. Como a nossa peça tem seção quadrada, a linha neutra passa exatamente no centro dela. Dessa maneira teremos que
Passo 4
Agora já temos a nossa fórmula
E os nossos valores
Basta que substituamos eles na nossa fórmula
Deixando o parêntese isolado teremos que
Isolando o valor de P
Resposta
Exercício Resolvido #10
Elaboração própria
Uma viga engastada em uma de suas extremidades sofre o carregamento mostrado abaixo. Sabendo que essa viga suportará uma carga triangular distribuída, determine o máximo valor que essa carga distribuída terá para que não haja rompimento da peça.
Passo 1
Como se trata de uma questão em que só consideraremos a contribuição dos esforços normais, e também temos uma resistência a tensão Normal, sabemos que a fórmula que devemos usar é a fórmula da flexão que é dada por
Mas podemos considerar algumas suposições, por exemplo, como queremos definir um valor máximo de carga, podemos fazer esse cálculo pelo módulo, ou seja, podemos retirar o sinal da nossa fórmula
Outra coisa que sabemos é que devemos usar a igualdade
Pois assim conseguiremos determinar o valor máximo que a peça aguenta sem romper.
Por fim, uma coisa que também temos que fazer é determinar o momento máximo que ocorre na nossa peça em função da nossa carga. Devemos usar o momento máximo pois queremos o ponto em que a viga será mais solicitada. Se ela suportar os esforços nesse ponto, aguentará em qualquer ponto.
Passo 2
Como a nossa viga está engastada, e todos os carregamentos maiores estão na mesma direção, o maior momento que a nossa viga estará sujeita ocorrerá na parede, ou seja, no ponto A.
Para determinarmos o valor desse momento devemos desenhar o nosso diagrama de corpo livre
Com o nosso diagrama de corpo livre devemos fazer o equilíbrio da nossa peça para podermos calcular as reações de apoio
Podemos então isolar o valor de , e dessa forma teremos que
Agora que já determinamos o valor da reação vertical, vamos calcular o momento em A
E esse momento que calculamos é o nosso momento máximo
Passo 3
Agora que já temos o valor do nosso momento, precisamos definir os outros dois valores da nossa fórmula, que são os valores do momento de inercia e do y.
Vamos primeiro definir o nosso momento de inércia. Como a nossa seção é quadrada, sabemos que o momento de inércia é dado por
Como é uma seção quadrada, sabemos que
Substituindo na nossa fórmula teremos que
Como já dissemos antes também precisamos do valor de y, com isso teremos que
Como queremos sempre o valor máximo, sempre usaremos o valor mais distante da linha neutra. Como a nossa peça tem seção quadrada, a linha neutra passa exatamente no centro dela. Dessa maneira teremos que
Passo 4
Agora já temos a nossa fórmula
E os nossos valores
Basta que substituamos eles na nossa fórmula
Deixando o parêntese isolado teremos que
Isolando o valor de P