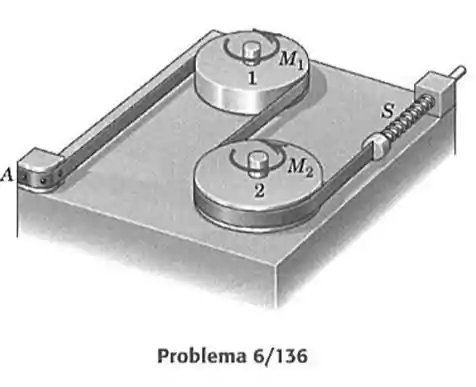
136- A fita flexível presa em A faz uma meia volta em torno de cada um dos tambores de 100m m de diâmetro e termina na mola S , que é ajustada para produzir uma força trativa de 40N sobre a fita. Calcule os torques M 1 e M 2 aplicados aos eixos dos tambores, de forma a girá-los ao mesmo tempo na direção mostrada. O coeficiente de atrito entre o tambor 1 e a fita vale 0.30 , e entre o tambor 2 e a fita vale 0.20 .

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.10 - Ex. 136

136- A fita flexível presa em faz uma meia volta em torno de cada um dos tambores de de diâmetro e termina na mola , que é ajustada para produzir uma força trativa de sobre a fita. Calcule os torques e aplicados aos eixos dos tambores, de forma a girá-los ao mesmo tempo na direção mostrada. O coeficiente de atrito entre o tambor e a fita vale , e entre o tambor e a fita vale .

Passo 1

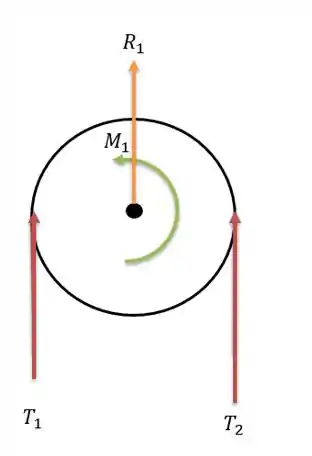
Vamos desenhar a polia e examinar fazer seu sistema de forças.

Onde a polia abraça metade da polia, tendo um ângulo de abraçamento igual a:

E o coeficiente de atrito entre a fita e a polia vale:

Além que se o sentido de movimento encontra-se no sentido anti-horário, logo para estarmos no limiar desse movimento com o atrito agindo temos que (pois ele agirá contra esse movimento), logo a fórmula para encontrar essa força de tração faltante será :

Como o raio dessa polia é de logo o momento presente nessa polia será de:

Passo 2

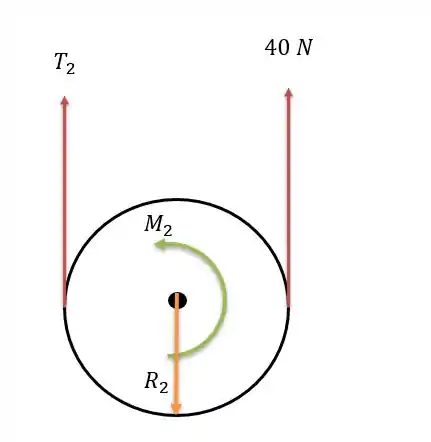
Agora podemos analisar o sistema de forças da polia :

Já para atender a essa condição com o atrito na polia temos que :

Onde o ângulo de abraçamento continua e que o atito na fita com a polia é de .

Porém vale .

Logo vale:

Logo o momento nessa polia valerá:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O carrinho de mão possui rodas com diâmetro de 80m m . Se uma caixa com massa de 500k g é colocada no carrinho, de modo que cada roda suporte uma mesma carga, determine a força horizontal P que precis

A polia de 5 kg tem diâmetro de 240 mm e o eixo tem diâmetro de 40 mm. Se o coeficiente de atrito cinético entre o eixo e a polia é μ k = 0,15 , determine a força vertical P na corda necessária para l

Uma polia com 80 mm de diâmetro e 1,25 kg de massa é suportada livremente em um eixo com 20 mm de diâmetro. Determine o torque M que deverá ser aplicado à polia para fazer com que ela gire com movimen

Resolva o Problema 8.120 se a força P for aplicada horizontalmente à esquerda.

Uma grande caixa, com 200 kg de massa, é empurrada pelo piso usando uma série de roletes com 150 mm de diâmetro para os quais o coeficiente de resistência ao rolamento é 3 mm no piso e 7 mm na superfí