Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.6 - Ex. 139

139. A massa de um sistema criticamente amortecido, que possui uma frequência natural ω n = 4   r a d / s , é liberada a partir do repouso com um deslocamento inicial x 0 . Determine o tempo t necessário para a massa atingir a posição x = 0,1   x 0 .

Passo 1

Bom, para um fator de amortecimento ζ = 1 , temos a seguinte solução:

x = ( A 1 + A 2 t ) e - ω n t

Temos que, para x 0 , no tempo t = 0 :

x 0 = A 1

Agora vamos derivar a solução x em relação ao tempo para encontrar a velocidade x ˙ :

d d t A 1 + A 2 t e - ω n t = d d t A 1 e - ω n t + d d t ( A 2 t e - ω n t )

d d t A 1 e - ω n t = - ω n A 1 e - ω n t

d d t A 2 t e - ω n t = A 2 e - ω n - ω n A 2 t e - ω n t

x ˙ = - ω n A 1 + A 2 t e - ω n t + A 2 e - ω n

Para x ˙ 0 , temos:

  x ˙ 0 = - ω n A 1 + A 2

Como partirmos do repouso e x 0 = A 1 :

- ω n x 0 + A 2 = 0

A 2 = ω n x 0

Passo 2

Agora, substituindo A 1 e A 2 na equação de posição x lá de cima:

x = ( x 0 + ω n x 0 t ) e - ω n t

x = x 0 ( 1 + ω n t ) e - ω n t

Passo 3

Trocando ω n na fórmula do x :

x = x 0 ( 1 + 4 t ) e - 4 t

E lembrando que x = 0,1   x 0 , temos que:

0,1   x 0 = x 0 ( 1 + 4 t ) e - 4 t

Simplificando e deixando tudo do mesmo lado, encontramos a função de t que chamaremos de f ( t ) :

f t = 4 t e - 4 t + e - 4 t - 0,1 = 0

Passo 4

E agora, derivamos a função f ( t ) encontrada, dividindo o processo em três partes, já que são três termos

d d t 4 t e - 4 t = 4 e - 4 t - 16 t e - 4 t

d d t e - 4 t = - 4 e - 4 t

d d t - 0,1 = 0   ( C o n s t a n t e )

Juntamos tudo e obtemos que:

f ' t = d d t 4 t e - 4 t + d d t e - 4 t + d d t - 0,1

f ' t = 4 e - 4 t - 16 t e - 4 t = - 4 e - 4 t

f ' t = - 16 t e - 4 t

Passo 5

Para finalizar, aplicando o método de Newton com o auxílio de um computador, na nossa f t , encontramos que:

t = 0,972   s

E se quiser conferir, basta substituir esse t na nossa função f t e ver se realmente tem condições de ser uma raiz da equação.

Para ter mais certeza ainda, vamos plotar o gráfico dessa função com auxílio de um computador e verificar em que ponto mais ou menos, a função toca o eixo das abscissas.

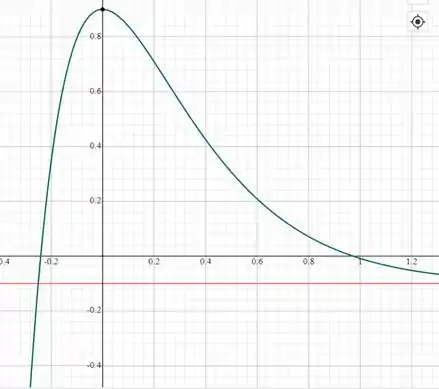
Parece que acertamos no final das contas!

Resposta

O tempo t para a massa atingir determinada posição é de:

t = 0,972   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o sistema do Prob. 8/3, determine a posição x da massa como uma função do tempo se a amssa é liberada a partir do repouso no instante de tempo t = 0 de uma posição 50m m à esquerda da posição de
Quando um colar de 3 kg é colocado sobre o prato da balança que está preso à mola de constante desconhecida, observa-se que a deflexão estática adicional é de 42 mm. Determine a constante da mola k em
Determine a frequência natural do sistema massa-mola, tanto em radianos por segundo quanto em ciclos por segundo (Hz).
O pistão vertical possui uma massa de 2.5 kg e é sustentado pelas duas molas, que estão sempre em compressão. Calcule a frequência natural f n de vibração do pistão se ele é deslocado da posição de eq
Mostre que a frequência natural de um sistema massa-mola orientado verticalmente, tal como o do Prob. 8/1, pode ser expressa comoω n = g δ e s t onde δ e s t é a deflexão estática.