Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 240
O deslocamento vertical do cilindro em metros é dado por onde é expresso em segundos. Calcule a aceleração descendente de do cilindro . Identifique o número de graus de liberdade.
Passo 1
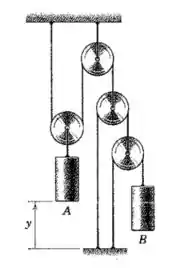
Esse é um daqueles problemas onde é importante ter uma mentalidade geométrica! Por isso vamos dar nome a algumas posições e comprimentos:
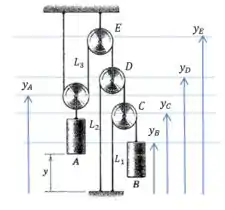
Atenção, os comprimentos , e se referem aquele trecho do cabo inteiro, incluindo a parte que passa para o outro lado da(s) polia(s). O por exemplo começa lá no teto e termina na polia .
Bem complicado né? Vamos organizar as informações que nós já temos. O enunciado deu a algtura do bloco função do tempo, vamos derivar para achar também a velocidade e a aceleração:
O próximo passo, assim como nos outros problemas que nós resolvemos por esse método “geométrico”, é escrever algumas expressões para os comprimentos e posições.
A vantagem de fazer isso é que os comprimentos , e são constantes! Então eles somem quando nós derivamos em relação ao tempo.
Passo 2
Então vamos lá, os comprimentos são:
Existe mais um pedaço do comprimento , que é a parte enrolada na polia. Mas como ela vai ser a mesma em todos os casos a gente pode ignorar sem problemas.
Ótimo, agora é só derivar (duas vezes, porque estamos procurando uma aceleração):
Passo 3
Ótimo, então ficamos com um sistema de três equações:
Mas veja bem: a polia está presa no teto! Isso quer dizer que ela não se move, e então .
Vamos isolar na primeira equação e substituir isso na segunda, aí vamos ficar com duas equações:
E agora vamos isolar na segunda equação e substitir isso na primeira:
Beleza, e nós já temos a aceleração do bloco , então :
Passo 4
E a questão ainda tem uma pegadinha final! Ela pediu a aceleração descendente do cilindro , ou seja, ele quer que a gente considere uma aceleração para baixo como negativa. Nesse caso, precisamos inverter o sinal:
Beleza, resolvido. Agora só falta responder a outra pergunta: quantos graus de liberdade tem esse sistema?
Bom, pelas equações que nós temos, se você tem o tempo você consegue determinar tudo, certo? Então ótimo, temos apenas um grau de liiberdade.
Resposta
A aceleração descendente do bloco é , e o sistema tem grau de liberdade.