Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 51

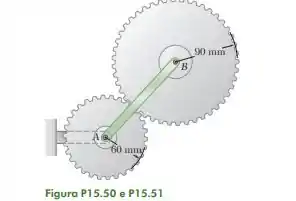
15.51. O braço AB gira a uma velocidade angular de 42 rpm no sentido horário. Determine a velocidade angular requerida da engrenagem A para que (a) a velocidade angular da engrenagem B seja de 20 rpm no sentido anti-horário, (b) o movimento da engrenagem B seja uma translação curvilínea.

Passo 1

Vamos matar mais essa?

O enunciado nos dá a velocidade angular de A B - .

ω A B = 42   r p m

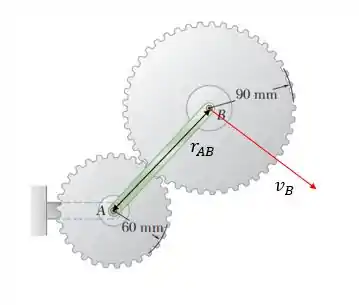
Com isso podemos calcular a velocidade tangencial do braço, ou seja, a velocidade que o ponto ao extremo do braço tem, mas o ponto ao extremo do braço é justamente o ponto B. Então podemos fazer

v B = ω A B ⋅ r A B

Então

v B = 42 ⋅ 150 = 6300   m m m i n

Passo 2

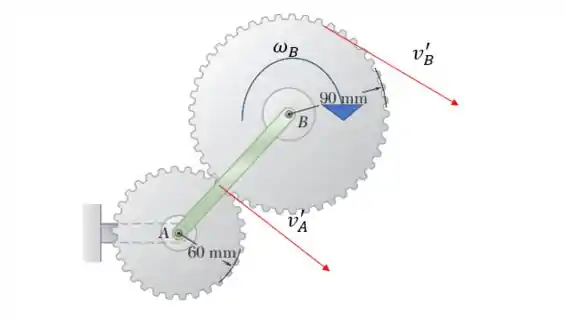
Na engrenagem B temos o seguinte:

ω B = 20   r p m

E

v B ' = ω B ⋅ r B

Logo

v B ' = 20 ⋅ 90 = 1800 m m m i n

Podemos fazer também

v A ' = v B ' + v B

Então

v A ' = 1800 + 6300 = 8100

Mas sabemos também que

v A ' = ω A ⋅ r A

Então

ω A = v A ' r A = 8100 60 = 135   r p m

Essa é a resposta do item (a).

Passo 3

Agora vamos para o item (b). Uma translação curvilínea significa que todas as partículas descrevem trajetórias curvilíneas iguais, ou seja, a engrenagem B não rotaciona.

ω B = 0

v B ' = 0

Então a velocidade na borda da engrenagem A vai ser a velocidade com que a engrenagem B gira em torno do ponto A. Podemos calcular essa velocidade assim:

v A ' = v B = ω A B r A B

v A ' = 42 ⋅ 150 = 6300   m m m i n

Então

ω A = v A ' r A = 6300 60 = 105   r p m

Resposta

a :   135   r p m b : 105   r p m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5/118) A tira flexível está presa em E ao setor rotativo e passa sobre a polia guia . Determine as velocidades angulares de A D e B D para a posição apresentada se a tira tem uma velocidade de 4 m / s
5/112) A barra O A possui uma velocidade angular no sentido anti-horário θ ' = 4r a d / s durante um intervalo de seu movimento . Determine a velocidade angular da barra A B e do setor B D para θ = 45
5/115) Um dispositivo que testa a resistência ao desgaste de dois materiais A e B é apresentado . Se a barra E O possui uma velocidade de 1,2m / s para a direita quando θ = 45 ° , determine a velocida
5/113) O cilindro hidráulico produz um movimento horizontal limitado do ponto A . Se v A = 4m / s quando θ = 45 ° , determine o módulo da velocidade de D e da velocidade angular ω de A B D para essa p
Para o instante representado, o elemento D gira com uma velocidade angular ω = 2r a d / s e sua ranhura está vertical. Também nesse instante, θ = 60 ° . Determine a velocidade da extremidade A da barr