Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 179

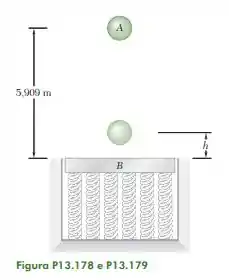
Uma esfera A de 1   k g é solta de uma altura de 5,909   m sobre uma placa B de 2   k g , que é suportada por um conjunto acondicionado de molas e que inicialmente está em repouso. Sabendo que o conjunto de molas é equivalente a uma única mola de k = 150   N / m , determine (a) o valor do coeficiente de restituição entre a esfera e a placa para que a altura h alcançada pela esfera após o rebote seja máxima, (b) o valor correspondente de h , (c) o valor correspondente da deflexão máxima da placa.

Passo 1

Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.

Primeiramente, usando a conservação de energia, temos que:

T 1 + V 1 = T 2 + V 2

Onde T   é a energia cinética e V   a potencial. Os índices 1 e 2 representam os instantes inicial e o momento do impacto. Substituindo:

0 + m A g h = 1 2 m A v A 2 + 0

Substituindo a altura dada e achando a velocidade v A :

v A = 3,28   m / s

Passo 2

Agora, usando a conservação de momento, temos que:

m A v A + m B v B = m A v A ' + m B v B '

Substituindo tudo, teremos:

- 10,767 = v A ' + 2 v B '

Aplicando o coeficiente de restituição, temos:

( v A - v b ) e =   v B ' - v A '

Substituindo:

v A ' - v B ' = - 10,767 e

Substituindo o valor de e   e resolvendo o sistema de 2 equações acima, teremos:

v A = 3,589 ( 2 e - 1 )

v B = - 3,589 1 + e

Agora, basta substituir naquela fórmula do passo 1 que trata da conservação de energia e isolar o h .   Fazendo isso:

h = v A ' 2 2 g

Substituindo os valores, teremos que para h   ser o máximo possível, teremos o maior e   possível, que é igual a 1.

Passo 3

Logo, substituindo e = 1   para achar h :

h = 0,06   m

Prontinho, mais uma questão finalizada.

Resposta

  1. e = 1
  2. h = 6   m m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ao pequeno rolamento de massa m é dada ima velocidade v 0 em A , paralela à borda horizontal de uma tigela lisa. Determine a intensidade da velocidade v da bola, quando esta houver caído uma distância
O bombeiro de 75k g está segurando uma mangueira que tem um diâmetro do bocal de 25m m e o diâmetro do corpo de 50m m . Se a velocidade da água na descarga é 18m / s , determine as forças normal e de
O carro de 75k g , de uma atração de parque de diversões, está conectado a uma lança telescópica giratória. Quando r = 4,5m , o carro move-se em uma trajetória horizontal circular a uma velocidade de
Um satélite de massa 700k g é lançado em uma trajetória de voo livre em torno da Terra a uma velocidade inicial v A = 10k m / s , quando a distância do centro da Terra é r A = 15M m . Se o ângulo de l
No instante que r = 1,5m , ao disco de 5k g é dada uma velocidade v = 5 m / s , perpendicular à corda elástica. Determine a velocidade do disco e a taxa de encurtamento da corda elástica no instante r