16.105. Se a está girando com uma velocidade angular = 6, determine a velocidade do centro da engrenagem no instante mostrado.
Passo 1
Como a haste está inserida numa rotação de eixo fixo, Fig. a. Podemos calcular a velocidade no ponto relacionando a velocidade angular da haste e seu comprimento :
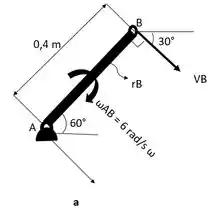
= .
Passo 2
Movimento geral do plano: Como a cremalheira é estacionária, ou seja, está imóvel, o da engrenagem está localizado no ponto de contato entre a engrenagem e a cremalheira, (Fig. b). Assim, e podem ser relacionados com os triângulos semelhantes mostrados na Fig. b.:
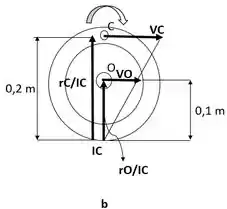
= =
=
Passo 3
A localização do para a haste é indicada na Fig. c. A partir da geometria mostrada, logo podemos determinar os segmentos de linha para e :
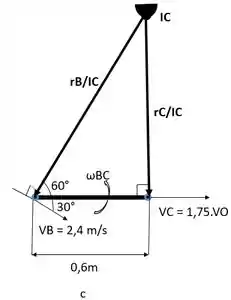
=
Logo...
Passo 4
Tendo as variáveis dependentes para achar a velocidade angular da haste determinada a partir da relação entre velocidade linear no ponto e seu respectivo segmento de linha:
= = =
Passo 5
Como a velocidade do centro depende do segmento de linha em e da velocidade angular da haste para transmitir o movimento de rotação, podemos determina-la da seguinte forma:
=