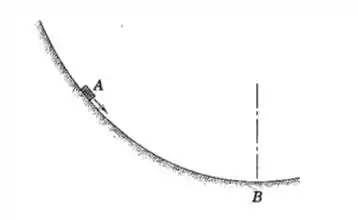
3/49) O pequeno bloco de desliza para baixo na trajetória curva e passa pelo ponto mais baixo com uma velocidade de . Se o raio de curvatura da trajetória em é de , determine a força normal exercida sobre o bloco pela trajetória neste ponto . É necessário o conhecimento das propriedades de atrito?
Passo 1
Bom galera, a primeira coisa que devemos fazer para resolver um exercício como esse é analisar as forças que atuam sobre o corpo . Utilizando o princípio do somatório das forças concorrentes , temos que :
Como a aceleração é normal à trajetória, temos que :
Passo 2
Agora basta substituirmos os valores que já conhecemos para acharmos a força normal :
Qualquer atrito/fricção existente não entraria na equação da força normal .
Resposta
Qualquer atrito/fricção existente não entraria na equação da força normal .
E aí , topa fazer mais exercícios com a gente?