Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 41
41. A barra é presa em e por cursores que podem se mover livremente nas hastes mostradas na figura. Se a corda é vertical , determine a tração na corda e as reações em e .
Passo 1
Primeiramente, para determinar o que o enunciado quer, temos que saber qual é a reação de um cursor e segundo a figura ele exerce uma força perpendicular a barra onde ele está preso.
Vamos também definir o sistema de coordenadas sendo o eixo na direção da haste que o ponto é preso. Assim, ficamos com o seguinte diagrama de forças.
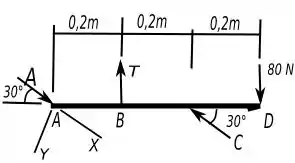
Então para achar o que o enunciado quer, vamos usar as equações de equilíbrio referente a força e ao momento ao nosso favor.
Para o cálculo do momento vamos considerar o sentido anti-horário como o sentido positivo.
Passo 2
Primeiro, vamos analisar a equação de equilíbrio referente a força na direção , então:
Passo 3
Agora vamos analisar a equação de equilíbrio referente ao momento em relação a , assim a força em , não contribui para esse cálculo de momento, já que ela passa pelo ponto. Então:
Passo 4
Agora vamos analisar a equação de equilíbrio referente ao momento em relação a , assim a força em , não contribui para esse cálculo de momento, já que ela passa pelo ponto. Então: