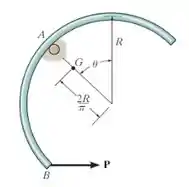
A argola semicircular fina de peso e centro de gravidade em é suspensa pelo pequeno piso em . Uma força horizontal é lentamente aplicada em . Se a argola começa a deslizar em quando , determine o coeficiente de atrito estátito entre a argola e o pino.
Passo 1
De início, vamos dar uma olhada no diagrama de corpo livre dessas questão para entendermos as forças que estão atuando.
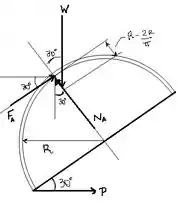
Passo 2
Quando nós temos um sistema em equilíbrio, o somatório das forças que atuam nesse sistema, em todos os eixos de referência ( é igual a zero. Vamos aplicar esse princípio na nossa questão! Adotando como direções positivas para cima e para direita, temos o seguinte:
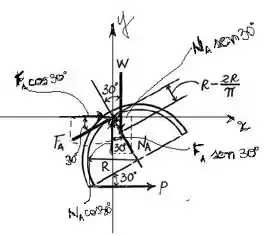
Passo 3
O somatório dos momentos em relação a um ponto, para o sistema em equilíbrio, deve ser igual a zero. Vamos calcular o momento em relação ao ponto e, assumindo como sentido positivo o anti-horário, temos:
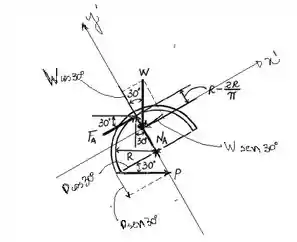
Temos aqui três equações e três incógnitas. Precisamos resolver esse sistema para que possamos encontrar o valor de .
Assim,
Passo 4
Vamos agora substituir o valor de na seguinte equação .
Resposta
O coeficiente de atrito estátito entre a argola e o pino é igual a: