A barra de , , é liberada do repouso quando . Determine sua velocidade angular quando . A mola permanece vertical durante o movimento e não está deformada quando .
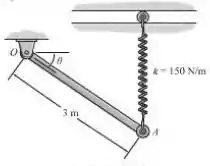
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
A conservação de energia é dada por:
Vamos analisar cada componente:
Considerando o ponto inicial e , temos:
Temos também que:
Como o sistema está em repouso no momento inicial, temos que e são nulos, logo:
Passo 2
Para o momento final, temos:
Temos que logo:
A parcela cinética final será:
Onde para uma barra de comprimento .
Como pode ser retratado como, , temos:
Logo:
Passo 3
Vamos aplicar conservação de energia: