Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 34

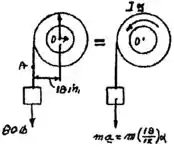
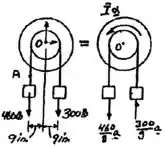
Cada uma das roldanas duplas mostradas na figura tem um momento de inércia de massa de 20 ∙ kg m2 e está inicialmente em repouso. O raio externo é de 500 mm e o interno de 250 mm. Determine (a) a aceleração angular de cada uma das roldanas, (b) a velocidade angular de cada uma das roldanas depois do ponto A na corda ter se deslocado 3 m.

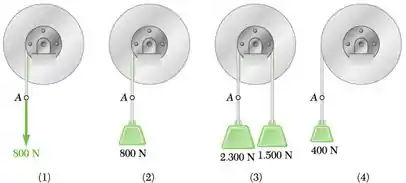
Passo 1

O exercício pede que a gente encontre a aceleração angular de cada uma das roldanas, (b) a velocidade angular de cada uma das roldanas depois do ponto A na corda ter se deslocado 3 m.

  1. + Σ M 0 = Σ M 0 eff :               160   lb 9 12   ft = 15   lb ∙ ft ∙ s 2 α

θ = 10   ft 9 12   ft = 13.333   rad

ω 2 = 2 α θ = 2 8   rad/ s 2 13.33   rad

Passo 2

  1. + Σ M 0 = Σ M 0 eff :               160 9 12 = 15 α + m a 9 12

    120 = 15 α + 160 32.2 9 12 α 9 12

    120 = 15 + 2.795 α

    α = 6.7435   rad/ s 2

θ = 10   ft 9 12 ft = 13.333   rad

ω 2 = 2 α θ

= 6.7435   rad/ s 2 13.333   rad

Passo 3

  1. + Σ M 0 = Σ M 0 eff :               460 9 12 - 300 9 12 = 15 α + 460 32.2 a 9 12 + 300 32.2 a 9 12

    120 = 15 α + 460 32.2 9 12 2 α + 300 32.2 9 12 2 α

    α = 4.2437   rad/ s 2

ω 2 = 2 α θ = 2 4.2437 13.333

Passo 4

  1. + Σ M 0 = Σ M 0 eff :               80 18 12 = 15 α + 80 32.2 a 18 12

    120 = 15 α + 80 32.2 18 12 2 α

    120 = 15 + 5.5901 α

    α = 5.828   rad/ s 2

θ = 10   ft 18 12   ft = 6.6667   rad

ω 2 = 2 α θ = 2 5.828   rad/ s 2 6.6667   rad

Resposta

Caso 1:

a )   α = 8   rad/ s 2  

b )   ω = 14.61   rad/ s  

Caso 2:

a )   α = 6.74   rad/ s 2  

b )   ω = 13.41   rad/ s  

Caso 3:

a )   α = 4.24   rad/ s 2  

b )   ω = 10.64   rad/ s 2  

Caso 4:

a )   α = 5.83   rad/ s 2  

b )   ω = 8.82   rad/ s  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante mostrado na figura, a velocidade angular das hastes de conexão BE e CF é de 6 rad/s no sentido anti-horário e está diminuindo a uma taxa de 12 rad/s2. Sabendo que o comprimento de cada has
Uma placa ABD e uma barra OB estão rigidamente conectadas e giram sobre a junta rotulada O com velocidade angular ω = ω x i ^ + ω x j ^ + ω z k ^ . Sabendo que v A =( 75m m / s ) i ^+( 350m m / s ) j
Resolva o Problema 15.184, considerando que ω x = 1,5r a d/ s .
No instante considerado, a antena de radar mostrada na figura gira em torno da origem das coordenadas com uma velocidade angular ω = ω x i ^ + ω y j ^ + ω z k ^ . Sabendo que v A y =300m m / s , v B y
No instante considerado, a antena de radar mostrada na figura gira em torno da origem das coordenadas com uma velocidade angular ω = ω x i ^ + ω y j ^ + ω z k ^ . Sabendo que v A x =10 0m m / s , v A