Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.5 - Ex. 121

A casca cilíndrica semicircular de raio r com espessura de parede pequena, porém uniforme, é colocada em oscilação com deslocamentos pequenos sobre a superfície horizontal. Se não ocorre deslizamento, determine a expressão para o período τ de cada oscilação completa.

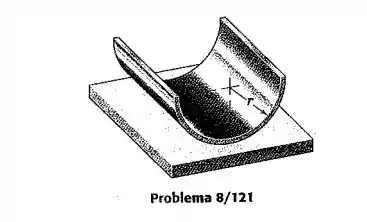
Passo 1

Para esse problema vamos usar as relações de conservação de energia para o estado inicial e o final e usaremos também expansão de Taylor para ângulos pequenos. Também usaremos o teorema dos eixos paralelos para descobrir o momento de inércia do cilindro.

Passo 2

Esse problema é basicamente um meio cilindro que fica oscilando em torno de seu ponto de equilíbrio estável. Sabemos que no seu estado inicial antes de começar a oscilar, sua energia potencial é máxima e sua cinética é mínima. Quando o cilindro para pelo ponto de equilibro, sua potencial é zero e sua cinética é máxima. Assim, temos que a conservação de energia nos dará que

T m á x = U m á x

Nossa potencial máxima é dada por U m á x = m ⋅ g ⋅ r - ⋅ 1 - cos ⁡ θ m á x = m ⋅ g ⋅ 2 ⋅ r π ⋅ 1 - cos ⁡ θ m á x . Usando expansão de Taylor para pequenos ângulos, ficamos que cos ⁡ θ m á x = 1 - θ 2 2 . Substituindo na potencial, temos que

U m á x = m ⋅ g ⋅ r ⋅ θ m á x 2 π

Analisando a energia cinética agora, temos que

T = 1 2 ⋅ I c ⋅ ω 2 = 1 2 ⋅ ω 2 ⋅ I → + m ⋅ r - r → 2 ⋅ ω 2

T = 1 2 ⋅ I o - m ⋅ r → 2 + m ⋅ r - r → 2 ⋅ ω 2 = m ⋅ r 2 ⋅ 1 - 2 π ⋅ ω 2

T = m ⋅ r 2 ⋅ 1 - 2 π ⋅ ω n ⋅ θ m á x 2

Substituindo na equação da conservação de energia, teremos que

m ⋅ r 2 ⋅ 1 - 2 π ⋅ ω n ⋅ θ m á x 2 = m ⋅ g ⋅ r ⋅ θ m á x 2 π

ω n = g r ⋅ π ⋅ 1 - 2 π

τ = 2 ⋅ π ω n = 2 ⋅ π ⋅ π - 2 ⋅ r g

Resposta

τ = 2 ⋅ π ⋅ π - 2 ⋅ r g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura 14-37 mostra um meio cilindro maciço e homogêneo, de massa M e raio R , em repouso sobre uma superfície horizontal. Se um dos lados deste sólido for ligeiramente empurrado para baixo e largad
Uma atiradeira gigante (hipotética) sofre um alongamento de 2,30m para lançar um projétil de 170g com velocidade suficiente ( 11,2k m / s ) para escapar da atração gravitacional da Terra. Suponha que
O disco possui um momento de inércia de massa I O em relação a O e é movido por uma mola de torção com constante K . A posição dos pequenos cursores, cada um dos quais possui uma m , é ajustável. Dete
A roda raiada com raio r , massa m e raio de giração centroidal k - rola sem deslizar sobre a inclinação. Determine a frequência natural de oscilação e examine os casos limites de k - = 0 e k - = r .
Calcule a frequência f n de oscilação vertical do sistema apresentado. A polia de 40kg tem um raio de giração em relação ao seu centro O de 200mm .