Exercícios de Energia no MHS - Lista de Exercícios Resolvida
Questão 1
Um oscilador harmônico possui frequência e amplitude
- Quais são os valores dos módulos da posição e da velocidade quando a energia potencial elástica for igual a energia cinética? (Suponha que no momento de equilíbrio)
- Quantas vezes isso ocorre em cada ciclo? Qual é o intervalo de tempo entre duas ocorrências?
- No momento em que o deslocamento é qual a fração da energia total do sistema referente a energia cinética e a qual corresponde a energia potencial?
Questão 2
Um sistema oscilatório bloco-mola possui uma energia mecânica de J uma amplitude de e uma velocidade máxima de . Determine:
(a) a constante elástica
(b) a massa do bloco
(c) a frequência da oscilação.
Ver solução completaQuestão 3
Determine a energia mecânica de um sistema bloco-mola com uma constante de e uma amplitude de oscilação de
Ver solução completaQuestão 4
No momento em que começa a ser observada (, uma partícula de massa ligada a uma mola ideal de constante se afasta da origem e sua energia potencial vale metade da energia mecânica total. Sobre sua constante de fase , podemos afirmar que:
Questão 5
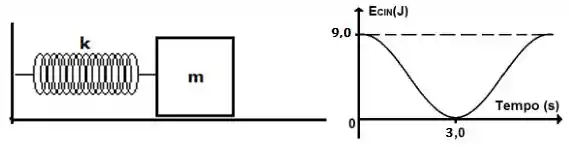
Um sistema massa-mola é colocado pra oscilar de modo que o gráfico abaixo mostra a energia cinética do bloco em função do tempo. Sabendo que a massa do sistema é M = 10Kg, qual é a amplitude do movimento em metros?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 6
Considere um oscilador harmônico simples, inicialmente na posição de equilíbrio, e as três condições abaixo:
I -
II -
III -
Marque a alternativa correta:
- Em todos os casos o corpo ficará sempre parado, pois já está na posição de equilíbrio.
- O corpo atingirá o deslocamento máximo em menos tempo no caso .
- O corpo atingirá o deslocamento máximo ao mesmo tempo nos casos e
- O corpo oscilará com a mesma amplitude nos casos e .
- A energia mecânica total do oscilador no caso é o dobro da do caso
Questão 7
No momento em que começa a ser observada (, uma partícula de massa ligada a uma mola ideal de constante se afasta da origem e sua energia potencial vale metade da energia mecânica total. Sobre sua constante de fase podemos afirmar que:
Questão 8
Um diafragma de um alto falante está oscilando em movimento harmônico simples de acordo com a equação , onde é dado em segundos.
- Qual é a frequência de oscilação do diafragma?
- Calcule a velocidade máxima do diafragma.
- Encontre a intensidade da aceleração máxima do diafragma.
- Se o movimento harmônico simples do diafragma possui uma constante elástica , qual é a energia total do diafragma?
Questão 9
Um corpo de massa está oscilando sobre um plano horizontal sem atrito preso a uma mola de constante elástica . Sabe-se que no instante inicial () o corpo passa na posição (em relação ao ponto de equilíbrio) com velocidade .
- Calcule a energia mecânica () do sistema.
- Encontre os valores da frequência angular e da amplitude () de oscilação do sistema.
- Descubra, através de equações adequadas, os valores da posição do corpo quando a energia cinética for o triplo da energia potencial.
- Sendo a posição da partícula dada por , determine a constante de fase (). Escreva a função com os valores numéricos e respectivas unidades.
- Obtenha o valor máximo da aceleração do corpo e da força máxima que a mola exerce sobre o corpo.
Questão 10
A figura a seguir mostra os gráficos da energia cinética em função da posição para três osciladores harmônicos que têm a mesma massa. Pode-se dizer que:
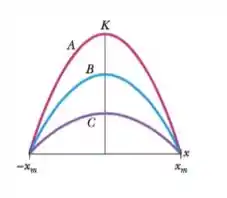
Os três osciladores tem o mesmo período de oscilação.
O oscilador completa uma oscilação em um tempo menor que os outros dois.
A frequência de oscilação associada à curva é menor que aquela da curva .
A constante elástica do oscilador é maior que a dos osciladores e , sendo a constante elástica do oscilador menor que a do oscilador .
A constante elástica do oscilador é maior que a do oscilador .
Ver solução completaQuestão 12
Um cilindro sólido de massa M = 4,0 kg está sobre uma superfície horizontal, preso pelo seu eixo a uma mola ideal horizontal de constante elástica k = 2,70 N/cm. O cilindro é afastado de 20,0 cm de sua posição de equilíbrio e abandonado a partir do repouso. Durante a oscilação o cilindro rola sem deslizar.
a) Mostre que o centro de massa do cilindro executa um movimento harmônico simples com período de .
b) Calcule as energias cinéticas de translação e de rotação do cilindro quando este passa pela posição de equilíbrio,
Ver solução completaQuestão 13
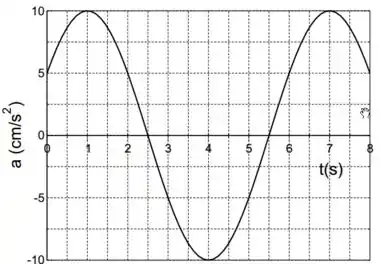
O gráfico abaixo mostra a aceleração em função do tempo de um corpo de massa preso a uma mola ideal de constante em movimento oscilatório. Justificando todas as respostas, determine:
- O período de oscilação.
- A amplitude do movimento.
- A expressão para o deslocamento em função do tempo, em relação ao ponto de equilíbrio.
- A velocidade do corpo quando
- A energia mecânica do sistema.
Questão 15
Considere o sistema abaixo formado por um bloco de massa e duas molas, cada uma de constante elástica . Este sistema está executando um movimento harmônico simples (MHS) cujo gráfico da posição como função do tempo também está ilustrado abaixo. Avalie como verdadeiras ou falsas as afirmações a seguir.
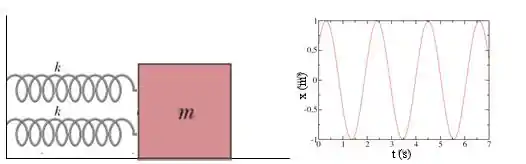
(I) Se na superfície da Terra, a frequência natural do sistema ´e , quando este é transportado para o espaço interestelar, a frequência ;
(II) Em , o sistema está se movendo com velocidade positiva e energia potencial diferente de zero;
(III) Como o sistema está executando um MHS, o período de oscilação é
(IV) Dado que no problema acima as molas estão associadas em paralelo, a frequência angular do MHS é
(V) Se a constante elástica de uma das molas fosse enquanto a da outra mola fosse , a frequência de oscilação do sistema seria o dobro.
(VI) Se agora há uma força dissipativa proporcional à velocidade se opondo ao movimento do sistema, as amplitudes de oscilação terão decaimento exponencial com o tempo e a frequência da oscilação será menor que a frequência de uma oscilação livre.
Ver solução completaQuestão 16
A figura mostra um bloco de massa que oscila sobre uma superfície horizontal, sem atrito, sob a ação de uma força elástica produzida por uma mola, da forma:
,
Onde indica a posição horizontal do bloco em um dado sistema de coordenadas, e são constantes e e .
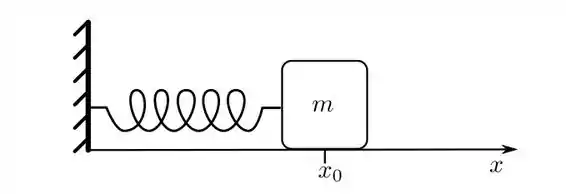
a) Qual a posição de equilíbrio do bloco, , tal que a mola encontra-se relaxada?
b) Encontre a equação diferencial de movimento para a posição do bloco.
c) Encontre a solução geral da equação encontrada no item anterior, sem impor condições iniciais.
d) Encontre a função horária se em o bloco está em e parte do repouso.
e) Esboce para as primeiras oscilações (decorridos dois períodos) do bloco, respeitando as condições do item . O bloco oscila em torno de que posição?
f) Determine a energia potencial elástica para este sistema. Esboce um gráfico para , indicando nele a posição de equilíbrio.
Ver solução completaQuestão 17
Um oscilador harmônico simples se constitui de uma massa presa à uma mola ideal de constante elástica . O sistema vibra com frequência angular e amplitude . O sistema é modificado e agora tem uma massa e é colocado para oscilar com amplitude . Em função de , a energia total no primeiro caso, e sua frequência angular , qual alternativa melhor expressa estas grandezas no segundo caso?
- e
- e
- e
- e
- e
Questão 18
Considere um oscilador harmônico simples, inicialmente na posição de equilíbrio, e as três condições abaixo:
I. (0) = 0;
II. (0) = v0;
III. (0) = 2v0.
Marque a alternativa correta:
(a) Em todos os casos o corpo ficará sempre parado, pois já está na posição de equilíbrio.
(b) O corpo atingirá o deslocamento máximo em menos tempo no caso III.
(c) O corpo oscilará com a mesma amplitude nos casos II e III.
(d) A energia mecânica total do oscilador no caso III é o dobro da do caso II.
(e) O corpo atingirá o deslocamento máximo ao mesmo tempo nos casos II e III.
Ver solução completaQuestão 19
Um bloco preso a uma mola executa um movimento harmônico simples. No instante, o bloco está exatamente no ponto intermediário entre a posição de equilíbrio da mola e a posição na qual a distensão da mola é máxima.Pode-se dizer que, nesse instante , a energia cinética do sistema massa-mola é:
- 3 vezes maior que a energia potencial elástica.
- 2 vezes maior que a energia potencial elástica.
- igual à energia potencial elástica.
- da energia potencial elástica.
- da energia potencial elástica.
- Impossível de ser comparada à energia potencial elástica.
Questão 20
Dois sistemas massa-mola, , oscilam de modo que suas energias mecânicas totais são iguais. Se , qual é a expressão que melhor relaciona suas amplitudes?
- Não há informações o suficiente pra se determinar a relação.
Questão 21
Um objeto de massa m oscila em um movimento harmônico simples. Sabendo-se que a distância máxima em relação ao ponto de equilíbrio é dada por A, que o período é T e que no instante t=0 o objeto está na origem, x=0, mas movendo-se na direção –x, mostre que (Obs: Estas equações são válidas para qualquer Oscilador Harmônico Simples):
d)A energia total do sistema pode ser dada por:
Ver solução completaQuestão 22
Um oscilador harmônico possui frequência e amplitude A.
a )Quais são os valores (módulos) da posição e da velocidade quando a energia potencial elástica for igual a energia cinética?
Ver solução completaQuestão 23
Um oscilador harmônico possui frequência e amplitude A.
b)Quantas vezes isso ocorre em cada ciclo e qual é o intervalo de tempo entre duas ocorrências consecutivas?
Ver solução completaQuestão 24
Um oscilador harmônico possui frequência e amplitude A.
c)Quando o deslocamento é a metade da amplitude, quais os valores das frações de energia cinética e energia potencial?
Ver solução completaQuestão 25
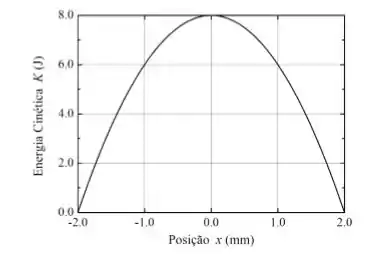
A figura abaixo mostra o gráfico da energia cinética de um sistema massa-mola em função da posição da massa. Determine o valor da constante elástica da mola em . Sabendo que o período de oscilação é s, encontre o valor da massa em . No instante , a massa encontra-se na posição com velocidade . Esboce o gráfico de sua posição para .
Questão 26
Em um ancoradouro, as marés fazem com que a superfície do oceano suba e desça uma distância (do nível mais alto ao nível mais baixo) em um movimento harmônico simples com um período de 12 h. Nas questões abaixo desconsidere efeitos gravitacionais.
Quanto tempo é necessário para que a água desça uma distância de a partir do nível mais alto?
A que distância do nível mais alto a superfície da água se movimenta com velocidade máxima? Justifique.
Ver solução completaQuestão 27
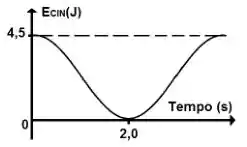
O gráfico ao lado mostra a energia cinética de um bloco conectado a uma mola em função do tempo. Sabendo que a massa do sistema é M = 5Kg, qual é a amplitude do movimento em metros?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
(j)
Ver solução completaQuestão 28
Uma partícula que pode-se mover livremente ao longo do eixo x têm uma energia potencial da forma
Onde é uma constante positiva. Para posições da partícula na região , onde também é uma constante positiva, pode-se dizer que:
- Para pequenos deslocamentos em relação a , o movimento é harmônico simpes com constante elástica
- Se x é não-nulo (), existe uma força que faz que a partícula fique cada vez mais distante de .
- Se a energia mecânica total é , a energia cinética é mínima em .
- Para pontos distantes da origem, a partícula está em equilíbrio instável.
- Para pequenos deslocamentos em relação a , o movimento é harmônico simples com constante elástica .
Questão 29
Uma massa presa na extremidade de uma mola ideal oscila com amplitude A, obedecendo à lei de Hooke. A que distância da posição de equilíbrio está a massa, no instante em que as energias potencial e cinética são iguais?
a)
b)
c)
d)
e)
Ver solução completaQuestão 30
I – Um oscilador harmônico simples é formado por um bloco preso a uma mola com constante elástica k = 200 N/m. O bloco desliza em uma superfície sem atrito,com ponto de equilíbrio em x = 0. O gráfico da velocidade do bloco em função do tempo, v(t), aparece na figura.
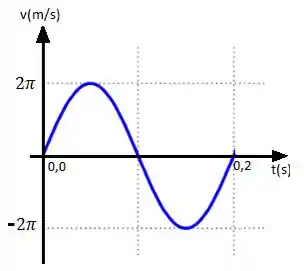
Considere:
Determine:
a) O período de oscilação do movimento, a frequência angular e a massa do bloco.
b) A amplitude do movimento.
c) A constante de fase e a função deslocamento x(t) do movimento.
d) A energia mecânica do oscilador.
e) O gráfico da energia cinética em função do tempo, indicando valores representativos das escalas (use o mesmo intervalo do gráfico acima).
Ver solução completaQuestão 31
Uma mola de constante elástica k = 12,0 N/m tem uma massa de 3,0 kg presa à sua extremidade. A massa é afastada +10,0 cm de sua posição de equilíbrio e então é liberada a partir do repouso. Qual é a velocidade da massa quando ela passa pela posição de equilíbrio?
a) +0,75 m/s;
b) –0,75 m/s;
c) +0,20 m/s;
d)–0,20 m/s;
e) –0,5m/s;
Ver solução completaQuestão 32
Em um oscilador harmônico simples como é afetada, pela duplicação da amplitude, cada uma das seguintes grandezas: período, energia total, velocidade máxima e aceleração máxima?
Ver solução completaQuestão 33
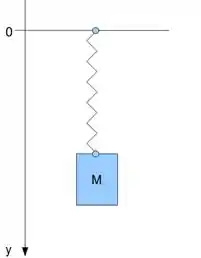
Uma massa M de é suspensa a uma mola de massa desprezível e constante elástica . A extremidade superior da mola é fixa. No repouso (sem a massa M) a mola tem comprimento.
- Qual é a posição da massa no equilíbrio?
- Sabendo que o período de oscilação pode ser aproximado pelo período de oscilação sem amortecimento, determinar o valor de ?
- Qual é a energia perdida durante as 5 oscilações?
No instante , a massa é afastada de da posição de equilíbrio e solta. A força de amortecimento é dada pela fórmula, onde é a velocidade da massa. Devido ao amortecimento, a amplitude cai da metade após 5 oscilações completas. No regime subcrítico, lembre-se de que a posição do objeto é dada por:
,
onde é a amplitude e é a constante de fase.
Questão 34
Um bloco de 1,0 kg está sobre uma superfície horizontal sem atrito e preso a uma mola ideal horizontal. Aplica-se uma força horizontal F = 20,0 N ao bloco para mantê-lo em repouso a 0,20 m de sua posição de equilíbrio (x = 0). Cessada a aplicação da força F o bloco executa um movimento harmônico simples. Determine:
a) O período e a frequência do movimento,
b) A aceleração máxima do bloco,
c) A velocidade do bloco ao passar pela primeira vez pela posição x = - 0,10 m.
d) A energia cinética do bloco em função de sua posição x.
Ver solução completaQuestão 35
O gráfico mostra a energia cinética em função do tempo para um sistema massa-mola com . Considere que o sistema seja descrito pela equação
E que , o deslocamente
a) Esboce no mesmo gráfico a energia potencial da mola Represente também no mesmo gráfico a energia total do sistema massa-mola
Determine:
b) A constante de fase .
c) A frequência angular
d) A amplitude de movimento
e) A massa do bloco.
Ver solução completaQuestão 36
Uma cantoneira maciça é formada por duas barras delgadas idênticas, cada uma de massa M e comprimento L, conectadas perpendicularmente. Na junção entre as barras há um pequeno orifício circular de raio desprezível. O conjunto é pendurado por meio de um pino de suspensão passando pelo orifício e em torno do qual a cantoneira pode girar sem atrito, como mostrado na figura, numa situação em que o sistema está em equilíbrio.
Quando a cantoneira é deslocada ligeiramente para a direita ou para a esquerda, ela oscila no plano da figura
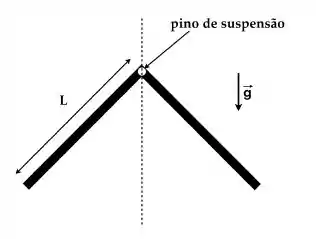
(a) Esboce o diagrama de forças externas que agem sobre a cantoneira num instante de tempo em que a linha que contém o CM desta faz um ângulo com a vertical.
(b) Adote um sistema de coordenadas com uma base de versores e determine o vetor torque total externo sobre a cantoneira na situação do item (a).
(c) No limite de pequenas oscilações, obtenha a equação diferencial para o ângulo , bem como a frequência natural das oscilações da cantoneira.
(d) Se o valor inicial para o ângulo é e a barra é liberada a partir do repouso, escreva a solução completa para o ângulo neste mesmo limite.
(e) Ainda no limite de pequenas oscilações, calcule as energias cinética e potencial da cantoneira como função do tempo. Verifique seu resultado, certificando-se de que a soma é constante. No limite de pequenos ângulos:
Ver solução completaQuestão 37
A posição como função do tempo para um oscilador levemente amortecido é descrita por , com todas as grandezas em unidades . A energia média inicial acumulada neste oscilador terá se reduzido a metade em que intervalo de tempo ?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 38
Um bloco de preso a uma mola oscila com frequência de e a amplitude de seu movimento é de .
Encontre o valor da constante elástica da mola, o valor máximo da velocidade do bloco e a energia total do sistema bloco-mola.
Encontre os módulos da velocidade e da aceleração do bloco quando ele passa pela posição .
Determine o menor tempo que o bloco leva para ir de até a posição
Em que posição a energia potencial elástica é metade da energia cinética?
Ver solução completaQuestão 39
Um objeto de que repousa em uma superfície horizontal sem atrito está preso a uma mola com . Objeto é deslocado horizontalmente a partir da posição de equilíbrio e recebe uma velocidade inicial de na direção da posição de equilíbrio. Determine a frequência do movimento, a energia potencial inicial do sistema massa-mola, a energia cinética inicial e a amplitude do movimento.
Ver solução completaQuestão 40
Determine a energia mecânica de um sistema bloco-mola com uma constante elástica de e uma amplitude de oscilação de .
Ver solução completaQuestão 41
A amplitude de um oscilador fracamente amortecido diminui de a cada ciclo. Que porcentagem da energia mecânica do oscilador é perdida em cada ciclo?
Ver solução completaQuestão 42
(Cap 13- Ex 72) Um bloco de massa igual a está submetido a uma força restauradora elástica e a constante da força é igual a . Faça um gráfico da energia potencial em função do deslocamento no intervalo de até . Em seu gráfico, adote a escala no eixo vertical e no eixo horizontal. O bloco inicia o movimento oscilatório com uma energia potencial igual a e uma energia cinética igual a . Examinando o gráfico, responda às perguntas seguintes. Qual é a amplitude da oscilação? Qual é a energia potencial quando o deslocamento é igual a metade da amplitude? Para qual deslocamento a energia potencial é igual a igual a energia cinética? Qual é o valor do ângulo de fase , sabendo que a velocidade inicial é positiva e o deslocamento inicial é negativo?
Ver solução completaQuestão 43
Considere um sistema massa-mola com um bloco de de massa preso à extremidade da mola e oscilando com amplitude de , repetindo o movimento a cada . A posição do bloco pode ser descrita por . Sabendo que após do início do movimento, o bloco atinge a sua posição máxima (positiva). Considere as afirmações como verdadeira ou falsa. (Considere ).
a) ( ) A frequência angular do movimento é de aproximadamente .
b) ( ) A constante elástica da mola é aproximadamente .
c) ( ) A energia cinética do sistema é máxima na posição máxima que o bloco atinge.
d) ( ) A energia mecânica do sistema é aproximadamente igual a .
e) ( ) A velocidade máxima que o bloco atinge é de aproximadamente .
f) ( ) Podemos determinar que a constante de fase é igual a .
Ver solução completaQuestão 44
A figura abaixo mostra as curvas obtidas em três experimentos fazendo um certo sistema bloco mola oscilar em um movimento harmônico simples. Pode-se dizer que:
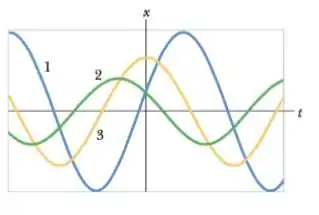
Em , a velocidade do bloco no experimento é maior que no experimento e maior que no experimento , sendo a velocidade do bloco nula no experimento .
A frequência angular do sistema nos três experimentos é diferente.
Em , a energia potencial da mola no experimento é maior que a energia potencial nos experimentos e , sendo a energia potencial no experimento menor que no experimento .
A energia cinética máxima do bloco no experimento é maior que no experimento , mas é menor que no experimento .
Em , a energia cinética do bloco no experimento é maior que no experimento .
Ver solução completaQuestão 45
Um objeto preso em uma mola realiza um movimento harmônico simples de amplitude . Quando o objeto se encontra a da posição de equilíbrio, qual fração de sua energia total é energia potencial?
- Dois terços.
- Um terço.
- Metade.
- Um quarto.
- Três quartos.
Questão 46
A figura mostra as curvas x(t) obtidas em três experimentos fazendo um dado sistema massa-
mola oscilar em um movimento harmônico simples. Ordene as curvas de acordo com a energia cinética do bloco no instante t = 0, começando pela maior.
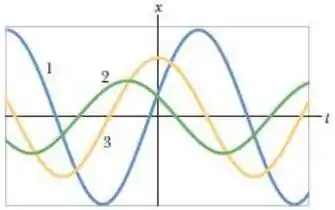
a) todas empatadas;
b) 2, depois 1 e 3 empatadas;
c) 1, 2, 3;
d) 2, 3, 1;
e) 3, 2, 1;
Ver solução completaQuestão 47
Um sistema massa-mola consiste de um corpo de massa e uma mola de constante elástica . No instante de tempo , a massa do sistema é colocada na posição ( em relação à posição de equilíbrio) com velocidade Desprezando quaisquer tipos de atrito, determine:
- A frequência de oscilação.
- A amplitude de movimento.
- A posição em função do tempo
- A velocidade em função do tempo
- A energia potencial elástica e a energia cinética em função do tempo.
Questão 48
(Cap 13 - Ex 31) Um corpo de sobre um trilho de ar horizontal, sem atrito, é preso a uma mola fixa ideal de constante . No instante que você efetua medições sobre o corpo, ele estará se movendo a e está a de seu ponto de equilíbrio. Use a conservação de energia para calcular a amplitude do movimento e a velocidade máxima do corpo. qual é a frequência angular das oscilações?
Ver solução completaQuestão 49
(Cap 13 - Ex 32) Um gato com massa igual a está preso por arreios a uma mola ideal de massa desprezível e oscila verticalmente em . A amplitude do movimento é . No ponto mais alto do movimento, a mola está na posição natural, ou seja, não está esticada. Calcule a energia potencial elástica da mola (considerando-a igual a zero quando não ela não está esticada) a energia cinética do gato, a energia potencial gravitacional do sistema em relação ao ponto mais baixo do movimento e a soma dessas três energias quando o gato está no ponto mais alto do movimento; no ponto mais baixo; no ponto de equilíbrio.
Ver solução completaQuestão 50
Um sistema massa-mola, movendo-se com um movimento harmônico simples, tem uma amplitude A. Quando a energia cinética da massa é o dobro da energia potencial armazenada na mola, qual é a posição x da massa?
a) A/√3;
b) A;
c) A/3;
d) 0;
e) nenhuma das respostas;
Ver solução completaQuestão 51
A figura ao lado mostra a velocidade de um bloco de massa preso a uma mola executando um movimento harmônico simples. Qual é a energia potencial elástica do sistema quando ? Sua resposta deve estar em Joules.
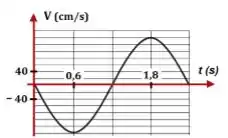
Ver solução completa
Questão 52
Um corpo oscila em movimento harmônico simples com amplitude . É correto afirmar que a energia mecânica do sistema
(A) é nula quando o corpo passa pelo ponto de equilíbrio.
(B) é nula quando o corpo atinge o deslocamento máximo.
(C) é máxima quando o corpo passa pelo ponto de equilíbrio.
(D) é mínima quando o corpo passa pelo ponto de equilíbrio.
(E) é constante.
Ver solução completaQuestão 53
Um sistema bloco-mola realiza um MHS com frequência . Se o ângulo de fase é e a posição do bloco é dada por , qual é a razão entre a energia cinética e a energia potencial no instante ?
a)
b) Nenhuma das demais alternativas
c)
d)
e)
Ver solução completaQuestão 54
Um pêndulo simples é constituído de uma massa de m = 1 kg suspensa por um fio de comprimento L com massa desprezível.
(a) [1,0] Escreva as equações de movimento para um ângulo de desvio em relação à posição de equilíbrio, justificando sua resposta. Supondo que o pêndulo execute pequenas oscilações em torno da posição de equilíbrio:
(b) [1,0] Determine o comprimento para que o período de oscilação seja de s.
(c) [1,0] Mostre que a energia total do pêndulo é constante.
Ver solução completaQuestão 55
Na figura mostrada, o bloco possui uma energia cinética de 3 J e a mola possui uma energia potencial elástica de 2 J quando o bloco está em x = +2 cm. Qual é a energia potencial elástica da mola quando o bloco está em está em x= -2 cm?
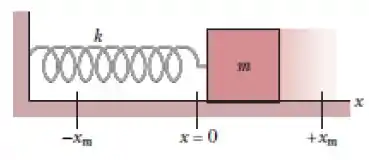
a) 5 J;
b) 2 J;
c) 1 J;
d) 0;
e) 1,5 J;
Ver solução completaQuestão 56
Um oscilador harmônico, composto de um bloco de massa e uma mola de constante elástica desconhecida, oscila de acordo com a função posição mostrada na figura. Considere que o oscilador é governado pela equação , com as grandezas no sistema internacional.
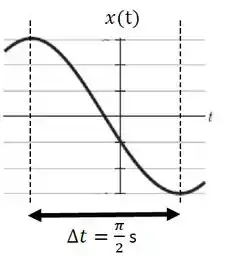
Determine:
(a) A frequência angular e a constante elástica da mola
(b) A constante de fase
(c) A(s) posição(ões) do bloco para que a energia potencial elástica seja metade da energia mecânica total
(d) O menor tempo para que o bloco vá da posição até o ponto de equilíbrio.
Ver solução completaQuestão 57
O gráfico da Figura abaixo mostra a aceleração de uma partícula que executa um movimento harmônico simples. Seja a amplitude do movimento, pode-se dizer que:
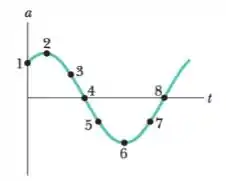
No ponto a partícula está na posição e no ponto a partícula está na posição
Nos pontos e a velocidade da partícula é nula.
No ponto a velocidade da partícula é negativa.
No ponto a partícula está na posição .
No ponto a partícula está entre e .
Ver solução completaQuestão 58
Duas massas e são postas para oscilar, presas a molas idênticas, respectivamente com energias e . Sobre os períodos de oscilação , as amplitudes do movimento e sobre as velocidades máximas atingidas , podemos afirmar que
- , ,
- , ,
- , ,
- , ,
- , ,
- , ,
- , ,
- , ,
Questão 59
Um oscilador harmônico possui frequência e amplitude
- Quais são os valores dos módulos da posição e da velocidade quando a energia potencial elástica for igual a energia cinética.( suponha que no momento de equilíbrio).
- Quantas vezes isso ocorre em cada ciclo? Qual é o intervalo de tempo entre duas ocorrências?
- No momento em que o deslocamento é qual a fração da energia total do sistema referente a energia cinética e a qual corresponde a energia potencial?
Questão 60
A maior velocidade de um corpo realizando movimento harmônico simples é atingida quando:
A) O módulo da aceleração assume seu valor máximo.
B) O deslocamento é máximo.
C) O módulo da aceleração assume seu valor mínimo.
D) A energia potencial assume seu valor máximo.
E) A energia cinética assume seu valor mínimo.
Ver solução completaQuestão 61
Uma plataforma gira com velocidade constante em torno do eixo perpendicular ao seu centro. O referencial girante tem origem no centro da plataforma e gira com a mesma velocidade . Uma mola ideal de constante está presa na origem do referencial com uma massa presa a outra extremidade. A massa pode deslocar-se sem atrito apenas radialmente apenas no interior de duas guias laterais. Inicialmente a massa está presa por um pino de segurança à uma distância da origem e a mola encontra-se relaxada.
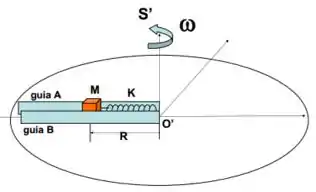
- Determine a posição de equilíbrio da massa a partir da posição inicial quando o pino de segurança for removido.
- Determine o vetor da força no referencial que a massa aplicará nas guias radiais quando passar pelo ponto de equilíbrio pela primeira vez.
- Qual será a força aplicada nas guias quando a massa atingir o seu deslocamento máximo?
Questão 62
Qual destas mudanças podemos fazer em um movimento harmônico simples para dobrar a velocidade máxima do movimento?
Escolha uma opção:
Quadruplicar a energia
Quadruplicar a amplitude
Quadruplicar o período
Multiplicar a energia por .
Duplicar o período.
Ver solução completaQuestão 63
Um malabarista de está pendurado por uma corda com constante elástica de , que pode ser modelada como uma mola. O malabarista, liberado quando a corda não está esticada, desce uma distância até parar. A amplitude de oscilação será:
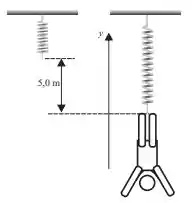
a)
b)
c)
d)
e)
Ver solução completaQuestão 64
Uma mola de constante elástica tem uma extremidade fixada numa parede e a outra, no centro de um disco de massa M, que pode movimentar-se numa superfície horizontal. No instante inicial, o disco está em repouso na posição de equilíbrio. A partir da posição de equilíbrio, o disco é puxado para a direita até que a elongação da mola seja . Depois de solto a partir da posição , o disco rola sem deslizar, realizando um movimento harmônico simples. A frequência angular do movimento é:
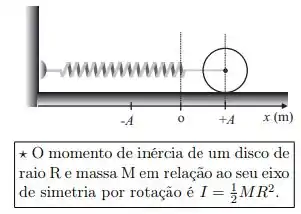
a)
b)
c)
d)
e)
Ver solução completaQuestão 65
A figura ao lado é o diagrama de energia potencial para uma trajetória de massa , que está sujeita à força conservativa , onde . A partícula é liberada do repouso na posição , com energia mecânica total , represnetada na figura por uma linha horizontal tracejada. Com base nestas informações podemos afirmar que a equação horária que descreve a velocidade da partícula em , é:
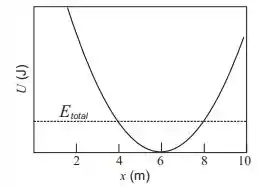
a)
b)
c)
d)
e)
Ver solução completaQuestão 66
Uma massa é presa a duas molas, ambas de constante elástica , conforme a figura abaixo. A coordenada mede o deslocamento da massa em relação à sua posição de equilíbrio, onde ambas as molas encontram-se relaxadas.
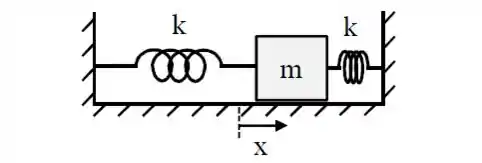
a)Use a segunda lei de Newton para obter a equação de movimento, que relaciona e
b) No instante a massa encontra-se em , com velocidade . Escrevendo a equação para o deslocamento instântaneo na forma determine os valores numéricos de .
c) Determine a energia total do sistema, nas condições do ítem (b).
Ver solução completaQuestão 67
Um bloco de massa está sobre uma superfície horizontal e sem atrito e preso a uma mola ideal de constante elástica . O bloco é puxado até distender a mola de um comprimento e em seguida abandonado do repouso. Qual das afirmativas é correta sobre o movimento harmônico simples que o sistema {bloco+mola} executa?
(A) O período do movimento é diretamente proporcional à distância .
(B) O período do movimento depende apenas da constante elástica .
(C) O período é o intervalo de tempo para o bloco percorrer a distância .
(D) A aceleração máxima do bloco é inversamente proporcional a .
(E) A energia cinética do bloco ao passar pela posição de equilíbrio é diretamente proporcional a .
Ver solução completaQuestão 68
Um bloco de massa m está preso a uma parede através de uma mola de constante elástica k e sobre um piso horizontal sem atrito. A figura 1 mostra a força F que a mola exerce sobre o bloco em função da sua posição . Nesta figura, O bloco é deslocado até e depois liberado. A figura mostra a oscilação resultante em termos da posição em função do tempo .
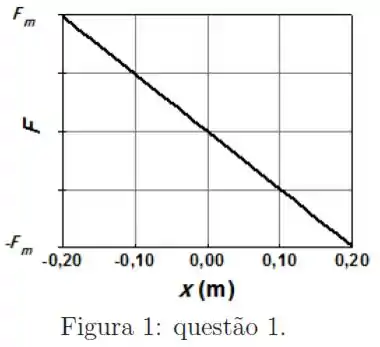
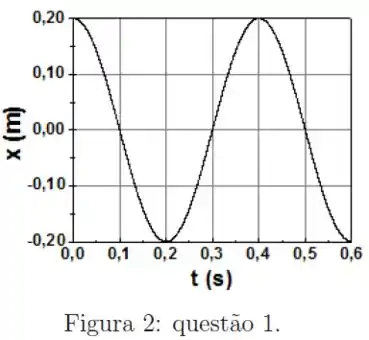
a)Calcule o valor de .
b)Calcule o valor da velocidade máxima do bloco.
Ver solução completaQuestão 69
Um sistema massa-mola oscila de acordo com a equação de movimento . Num dado instante de tempo, a massa que pesa está deslocada da posição de equilíbrio com velocidade de . Qual a energia mecânica armazenada no sistema?
Ver solução completaQuestão 70
A figura mostra os gráficos da energia cinética K em função da posição x para três osciladores harmônicos do tipo bloco-mola que têm a mesma massa e que descrevem movimentos harmônicos simples. Pode-se dizer que:
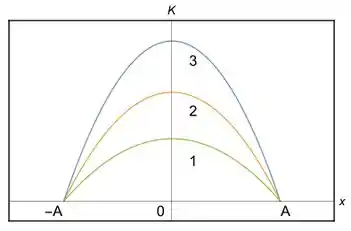
(a) A constante elástica do oscilador 2 é maior que a do oscilador 3.
(b) O período de oscilação associado ao oscilador 1 é menor que aquele dos osciladores 2 e 3.
(c) O oscilador 3 completa uma oscilação em um tempo menor que os outros dois.
(d) A constante elástica do oscilador 3 é maior que a dos osciladores 1 e 2, sendo a constante elástica do oscilador 2 menor que a do oscilador 1.
(e) Os três osciladores tem a mesma freqüência de oscilação.
Ver solução completa
