Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 14.1 - Ex. 103

A figura 14-37 mostra um meio cilindro maciço e homogêneo, de massa M e raio R , em repouso sobre uma superfície horizontal. Se um dos lados deste sólido for ligeiramente empurrado para baixo e largado, ele oscilará em torno de sua posição de equilíbrio. Determine o período desta oscilação.

Passo 1

Se não conseguiu resolver essa, não desanima, porque é casca grossa demais!!! Vamos com bastante calma.

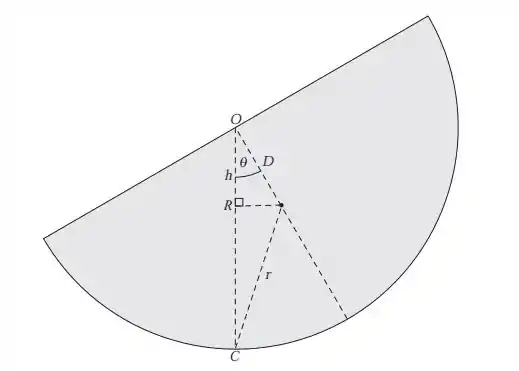
Primeiro representei o cilindro quando está torto, ao ser empurrado para baixo.

Vamos escrever a energia da situação:

E = U p o t e n c i a l + K r o t a ç ã o

E = M g D - h + 1 2 I c ω 2

E = M g D - D c o s θ + 1 2 I c d θ d t 2

Passo 2

O momento de inércia de um cilindro sólido, por um eixo perpendicular à sua face, e passando pelo centro, é:

I c i l i n d r o = 1 2 2 M R 2 = M R 2

Nessa fórmula, M é a massa de meio cilindro. Então, o momento de inércia de meio cilindro será:

I 0 = I c i l i n d r o 2 = M R 2 2

Agora vamos usar o teorema dos eixos paralelos para encontrar o momento de inércia em relação ao centro de massa.

I 0 = I c m + M D 2

I c m = M R 2 2 - M D 2

Agora, para achar o momento de inércia em relação ao ponto C da figura.

I C = I c m + M r 2 = M R 2 2 - D 2 + r 2

Pela lei dos cossenos,

r 2 = R 2 + D 2 - 2 R D c o s θ

Substituindo na expressão do momento:

I c = M R 2 3 2 - 2 D R c o s θ

Passo 3

Agora voltamos na expressão da energia!

E = M g D ( 1 - c o s θ ) + 1 2 M R 2 3 2 - 2 D R c o s θ d θ d t 2

Usando o polinômio de Taylor para c o s θ , vamos aproximar:

c o s θ = 1 - θ 2 2

Daí,

E = M g D θ 2 2 + 1 2 M R 2 3 - D R 2 - θ 2 d θ d t 2

Como θ 2 ≪ 2 , vamos desprezá-lo na segunda parcela da equação:

E = M g D θ 2 2 + 1 2 M R 2 3 - 2 D R d θ d t 2

A energia é constante. Então se a gente derivar com relação ao tempo, ela tem que dar 0 , certo?! Derivando...

M g D θ + M R 2 3 - 2 D R d 2 θ d t 2 = 0

d 2 θ d t 2 + g D R 2 3 2 - 2 D R θ = 0

Ou seja, um movimento harmônico com:

ω 2 = g D R 2 3 2 - 2 D R

Passo 4

Agora vamos achar o centro de massa do meio cilindro.

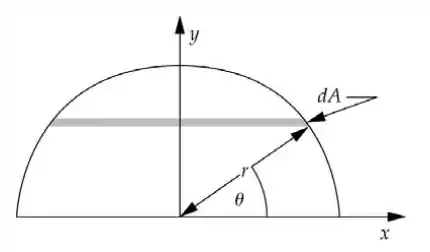
Por simetria, x c m = 0 . Para achar o y , vamos fazer:

y c m = D = ∫ y σ d A M

y = r s e n θ

d A = r d θ d r

Agora é só integrar com respeito às duas variáveis, famosa integral dupla!

y c m = D = σ M ∫ 0 R ∫ 0 π r 2 s e n θ d θ d r

Resolvendo, vamos obter:

D = 2 σ M ∫ 0 R r 2 d r

D = 2 σ 3 M R 3

Mas a massa é função de R e σ !

D = 2 σ 3 1 2 σ π R 2 R 3

D = 4 R 3 π  

Passo 5

Substituindo na expressão do ω :

ω 2 = g 4 R 3 π R 2 3 2 - 2 4 R 3 π R

ω 2 = 8 9 π - 16 g R  

Como T = 2 π / ω :

T = 2 π 9 π - 16 8 R g

T = 7.78 R g

Resposta

T = 7.78 R g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O comprimento da mola é ajustado de modo que a posição de equilíbrio do braço é horizontal conforme mostrado. Despreze a massa da mola e do braço e calcule a frequência natural f n para pequenas oscil
A casca cilíndrica semicircular de raio r com espessura de parede pequena, porém uniforme, é colocada em oscilação com deslocamentos pequenos sobre a superfície horizontal. Se não ocorre deslizamento,
A haste esbelta uniforme de comprimento 2 ⋅ b é sustentada no plano horizontal por uma suspensão bifilar. A haste é colocada em oscilação com ângulos pequenos em torno do eixo vertical através de seu
Um furo de raio R / 4 é perfurado através de um cilindro de raio R para formar um corpo de massa m como mostrado. Se o corpo rola sobre a superfície horizontal sem deslizar, determine o período τ para
100. A energia potencial V de um sistema massa-mola linear é dada, em joules, por 64 x 2 , onde x é o deslocamento em metros, medido a partir da posição de equilíbrio neutra. A energia cinética T do s