Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 57

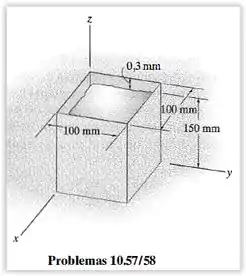
A cavidade de um corpo rígido liso está cheia com alumínio 6061 -   T 6 líquido. Quando frio, o líquido fica a 0,3   m m da parte superior da cavidade. Se essa parte superior for coberta e a temperatura aumentar 110 ° C , determine as componentes da tensão σ x , σ y e σ z no alumínio. Dica: Use as Equações 10.18 com um termo adicional α Δ T para a deformação (Equação 4.4 ).

Passo 1

E aí, galera! Vamos resolver esse problema?

O enunciado pede que determinemos as componentes da tensão σ x , σ y e σ z no alumínio se a parte superior da caixa for coberta e a temperatura aumentar 110 ° C . Nos dá como dica usar a equação 10.18 e adicionar o termo α Δ T nela.

Dados tabelados:

Coeficiente de dilatação linear do alumínio:

α a l = 24 ⋅ 10 6   ° C - 1

Módulo de elasticidade:

E a l = 68,9 ⋅ 10 9   G P a

Coeficoente de Poisson:

v = 0,35

Passo 2

Antes de fazermos as substituições, é importante observar que só vamos ter deformação no eixo z . O conteúdo da caixa tem altura inicial de 150   m m e depois preenche toda a caixa, passando a ter 150.3   m m , ou seja:

L 0 = 0,15   m

L = 0,1503   m

Diante disso, podemos calcular ϵ z .

ϵ z = L - L 0 L 0

ϵ z = 0,1503 - 0,15 0,015

ϵ z = 0,002

Passo 3

Vamos então às equações 10.18 !

Para a deformação no eixo x , temos:

ϵ x = 1 E σ x - v σ y + σ z + α Δ T

0 = 1 68,9 ⋅ 10 9 σ x - 0,35 σ y + σ z + 24 ⋅ 10 - 6 ⋅ 110

σ x - 0,35 σ y + σ z = - 2,64 ⋅ 10 - 3 ⋅ 68,9 ⋅ 10 9

σ x - 0,35 σ y - 0,35 σ z = - 181,89 6 ⋅ 10 6

Para a deformação no eixo y :

ϵ y = 1 E σ y - v σ x + σ z + α Δ T

0 = 1 68,9 ⋅ 10 9 σ y - 0,35 σ x + σ z + 24 ⋅ 10 - 6 ⋅ 110

σ y - 0,35 σ x + σ z = - 2,64 ⋅ 10 - 3 ⋅ 68,9 ⋅ 10 9

σ y - 0,35 σ x - 0,35 σ z = - 181,896 ⋅ 10 6

Para a deformação no eixo z :

ϵ z = 1 E σ z - v σ x + σ y + α Δ T

0,002 = 1 68,9 ⋅ 10 9 σ z - 0,35 σ x + σ y + 24 ⋅ 10 - 6 ⋅ 110

1 68,9 ⋅ 10 9 σ z - 0,35 σ x + σ y = - 6,4 ⋅ 10 - 4

σ z - 0,35 σ x + σ y = - 6,4 ⋅ 10 - 4 ⋅ 68,9 ⋅ 10 9

σ z - 0,35 σ x - 0,35 σ y = - 44,096 ⋅ 10 6

Passo 4

Agora é so resolver o sistema de três equações e três incógnitas, que você chegará ao resultado!

σ x - 0,35 σ y - 0,35 σ z = - 181,896 ⋅ 10 6 σ y - 0,35 σ x - 0,35 σ z = - 181,896 ⋅ 10 6 σ z - 0,35 σ x - 0,35 σ y = - 44,096 ⋅ 10 6

σ x = - 39,46592 ⋅ 10 9 81 = - 487,23 ⋅ 10 6   P a

σ y = - 39,46592 ⋅ 10 9 81 = - 487,23 ⋅ 10 6   P a

σ z = - 3 1,19792 ⋅ 10 9 81 = - 385 , 159 ⋅ 10 6   P a

Resposta

σ x = - 487,23   M P a

σ y = - 487,23   M P a

σ z = - 385,159   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A haste plástica de acrílico tem 200m m de comprimento e 15m m de diâmetro. Se uma carga axial de 300N for aplicada a ela, determine a mudança em seu comprimento e em seu diâmetro. E p = 2,70G P a , v
O bloco é feito de titânio T i - 6 A 1 - 4 V . É submetido a uma compressão de 1,5m m ao longo do eixo y , e sua forma sofre uma inclinação de θ =89,7 ° . Determine ϵ x , ϵ yeγ x y .
O cubo do Problema 2.91, de um material compósito, é impedido de se deformar na direção z e é alongado na direção x em 0,035 mm por uma força de tração na direção x. Determine (a) as tensões σ x , σ y
Um cubo, de um material compósito, com 40 mm de lado e as propriedades mostradas na figura é feito de polímeros com fibras de vidro alinhadas na direção x. O cubo é impedido de se deformar nas direçõe
Um suporte isolador de vibração consiste em uma barra A de raio r 1 e um tubo B de raio interno r 2 , colado a um tubo de borracha de 80 mm de comprimento com um módulo de elasticidade transversal G =