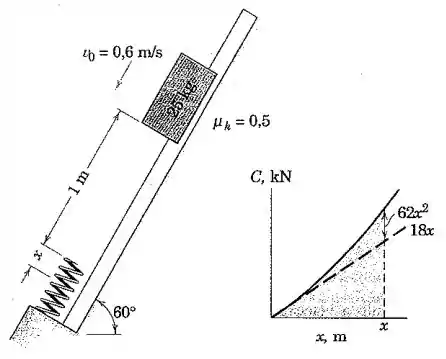
O cursor de na posição mostrada tem uma velocidade inicial sobre o trilho inclinado e desliza sob a influência da gravidade e do atrito. O coeficiente de atrito dinâmico entre o cursor e o trilho é de . Calcule a velocidade do cursor quando este passa a posição para a qual a mola está comprimida de uma distância . A mola oferece uma resistência à compressão e é conhecida como uma mola com “endurecimento”, uma vez que sua rigidez aumenta com a deflexão como mostrado no gráfico anexo.
Passo 1
Temporariamente, vamos desconsiderar a força devida à mola. Então, o diagrama de forças que agem no bloco seria similar ao de um plano inclinado:
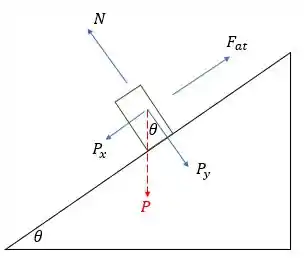
Na direção perpendicular à superfície, a componente do peso e a normal se equilibram:
Na direção paralela à superfície, a outra componente do peso e a força de atrito atuam, de modo que a força resultante (desconsiderando força elástica) é:
Passo 2
A força que calculamos é uma força constante, e portanto o trabalho realizado por ela será:
Porém, a força devida à mola não é constante, de modo que seu trabalho é:
Portanto, o trabalho total realizado sobre o cursor é:
Passo 3
Lembrando que o trabalho total realizado sobre o cursor é igual à sua variação de energia cinética, temos: