Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.6 - Ex. 115
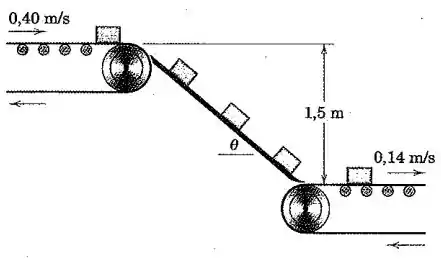
No projeto de um sistema de esteiras transportadoras, pequenos blocos metálicos são descarregados com uma velocidade de sobre uma rampa pela esteira transportadora superior mostrada. Se o coeficiente de atrito dinâmico entre os blocos e a rampa é de , calcule o ângulo que a rampa deve fazer com a horizontal para que os blocos sejam transferidos sem deslizar para a esteira transportadora inferior que se move na velocidade de .
Passo 1
Primeiramente, observe o seguinte diagrama de forças sobre o bloco:
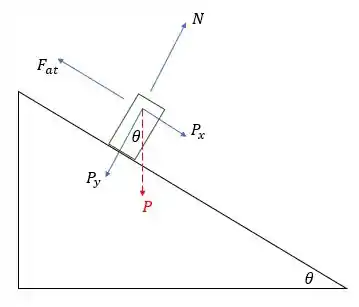
Na direção perpendicular à superfície, a componente do peso e a normal se equilibram, de modo que:
Na direção paralela à superfície, a outra componente do peso e a força de atrito atuam, de modo que a força resultante é:
Passo 2
Sabendo da força resultante na direção do movimento, calculamos o trabalho total:
Por outro lado, considerando que o bloco não desliza quando chega à esteira inferior, ou seja, que ele chega com a mesma velocidade da esteira, , obtemos a variação da energia cinética:
Passo 3
Como a variação da energia cinética de um corpo é igual ao trabalho total realizado sobre ele, temos: