Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 12
Determine as cargas internas resultantes que agem sobre: seção e seção . Cada seção está localizada no centroide, ponto .
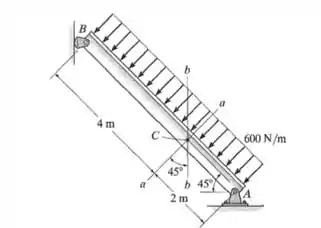
Passo 1
Primeiro vamos fazer o DCL para o segmento BA
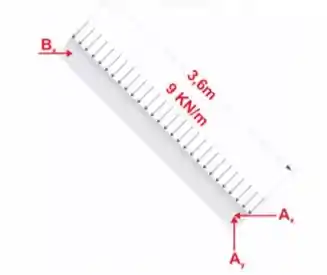
Como podemos ver, temos que transformar a carga ilustrada em uma carga concentrada. Para isso, basta multiplicar a carga pela distância em que ela é aplicada.
E o seu centro de atuação é na metade do retângulo, ou seja, com . Decompondo esta força, temos.
A para altura entre o ponto A e B:
Fica assim:
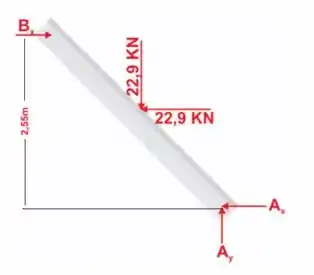
Passo 2
Depois, vamos usar as equações de equilíbrio e momento
Passo 3
Agora, vamos repetir o processo do primeiro passo para o segmento BC e decompor , para encontrarmos as cargas que agem sobre a seção
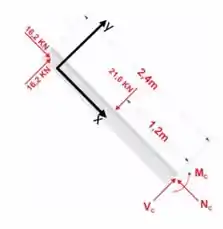
Passo 4
Vamos usar as equações de novo.
Passo 5
O processo é análogo para a seção , diferindo que a força decomposta é a dada
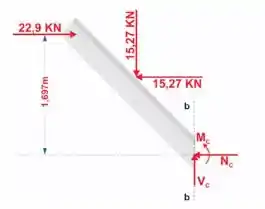
Resposta
Seção :
Seção