Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 35

Determine as coordenadas do centroide por integração em termos de a e h :

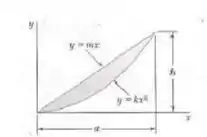
Passo 1

Fala aí galera, vamos para mais um problema de estática. Podemos ver que o centroide da área sombreada será o centroide do triângulo pela sua área menos do centroide da parábola pela sua área, divididos pela área do triângulo menos a da parábola. O primeiro passo é determinar a relação entre x   e y . Neste caso, sabemos que no caso do triângulo:

y = K x

h = K a

k = h a

Logo:

y = h a x

x = a y h

Agora, vamos utilizar a fórmula abaixo:

x - = ∫ x d A ∫ d A  

Agora, vamos pegar um elemento retangular infinitesimal de área:

d A = y d x

Logo:

x - = ∫ x d A ∫ d A   = ∫ 0 a x y d x ∫ 0 a y d x = ∫ 0 a h a x ² ∫ 0 a h a x d x = h a 2 3 h a 2 = 2 a 3

Já para a coordenada y :

y - = ∫ y d A ∫ d A  

Onde:

d A = y d x

Logo:

y - = ∫ y 2 d A ∫ d A   = ∫ 0 a y 2 2 d x ∫ 0 a h x a d x = ∫ 0 a h 2 x 2 2 a 2 d x ∫ 0 a h x a d x = h ² a 6 a h 2 = h 3

Passo 2

Já no caso da parábola:

y = k x 2

y k = x

Agora, vamos utilizar a fórmula abaixo:

x - = ∫ x d A ∫ d A  

Agora, vamos pegar um elemento retangular infinitesimal de área:

d A = y d x

Logo:

x - = ∫ x d A ∫ d A   = ∫ 0 a x y d x ∫ 0 a y d x = ∫ 0 a k x ³ d x ∫ 0 a k x ² d x = k a 4 4 k a 3 3 = 3 a 4

Já para a coordenada y :

y - = ∫ y d A ∫ d A  

Onde:

d A = y d x

Logo:

y - = ∫ y 2 d A ∫ d A   = ∫ 0 a y 2 2 d x ∫ 0 a y d x = ∫ 0 a k ² x 4 2 d x ∫ 0 a k x ² d x = a 5 k 2 10 k a 3 3 = 3 a 2 k 10

Passo 3

Portanto, agora basta fazer os cálculos enunciados no começo:

x - = 2 a 3 × a h 2 - 3 a 4 × k a 3 3 a h 2 - k a 3 3 = 4 a h - 3 a 3 k 2 3 h - 2 k a 2

y - = h 3 × a h 2 - 3 a 2 k 10 × k a 3 3 a h 2 - k a 3 3 = 10 h 2 - 6 a 4 k 2 10 3 h - 2 k a 2

Como o problema pede as coordenadas em função de a e h, temos que substituir o k por:

k = h a 2

Logo:

x - = 4 a h - 3 a 3 k 2 3 h - 2 k a 2 = a 2

y - = 10 h 2 - 6 a 4 k 2 10 3 h - 2 k a 2 = 4 h 10 = 2 h 5

Resposta

x - = a 2

y - = 2 h 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centroide y - da área sombreada.
Determine a localização r - do centroide C para a metade da lemniscata, r 2 = 2 a 2 cos ⁡ 2 θ ,- 45 ° ≤ θ ≤ 45 ° .
A placa de aço tem 0,3m de espessura e densidade de 7850k g / m 3 . Determine a localização de seu centro de massa. Além disso, determine as reações no pino e no apoio de rolete.
Se a densidade em qualquer ponto na placa de um quarto de círculo é definida por ρ = ρ 0 x y , em que ρ 0 é uma constante, determine a massa e localize o centro de massa x - , y - da placa. A placa te
Localize o centroide x - da área.