Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 30
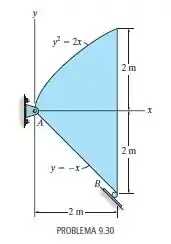
A placa de aço tem de espessura e densidade de . Determine a localização de seu centro de massa. Além disso, determine as reações no pino e no apoio de rolete.
Passo 1
Oi tudo bem? Vamos resolver este exercício.
Sabemos que o ângulo de fricção é dado por:
Portanto:
O ângulo de avanço do parafuso é dado por:
Substituindo os dados, temos que:
Passo 2
Agora vamos calcular o menor torque necessário para afrouxar o parafuso. Temos que:
Logo:
Resposta
Exercícios de Livros Relacionados
Determine a posição do centro de massa da casca cilíndrica com uma extremidade semicircular fechada. A casca é em chapa de metal com massa de 24k g / m 2 , e a extremidade em chapa de metal com massa
Determine as coordenadas do centro de massa do corpo homogêneo mostrado. O furo está centrado na superfície horizontal superior.
Determine as coordenadas do centroide da área sombreada.
Determine as coordenadas x e y do centroide da área sombreada.
O conjunto mostrado é formado por uma haste uniforme. Para qual valor do comprimento l o centro de massa estará localizado a uma altura de 3 r 4 acima da superfície de suporte?