Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 25
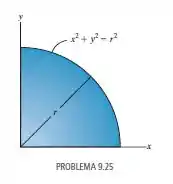
Se a densidade em qualquer ponto na placa de um quarto de círculo é definida por , em que é uma constante, determine a massa e localize o centro de massa da placa. A placa tem uma espessura .
Passo 1
Oi tudo bem? Vamos resolver este exercício.
Sabemos que o ângulo de fricção é dado por:
Portanto:
O ângulo de avanço do parafuso é dado por:
Substituindo os dados, temos que:
Passo 2
Agora vamos calcular o menor torque necessário para afrouxar o parafuso. Temos que:
Logo:
Resposta
Exercícios de Livros Relacionados
O conjunto soldado é feito de uma haste uniforme pesando 0,370l b por pé de comprimento e a placa semicircular pesando 8l b por pé quadrado. Calcule as coordenadas do centro de gravidade da montagem.
Determine as coordenadas x , y e z do centro de massa da forma de chapa de metal mostrada.
Determine a coordenada z do centróide do sólido retangular com o orifício hemisférico. O centro do hemisfério está centrado na face superior do sólido e z é medido para cima a partir da face inferior.
Determine a coordenada z do centróide do sólido retangular com o segmento esférico (menos de um hemisfério) removido. O centro do hemisfério do qual o segmento é uma porção está localizado a uma distâ
Determine as coordenadas do centro de massa da montagem soldada de hastes delgadas uniformes feitas do mesmo estoque de barras.