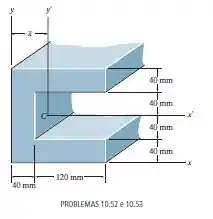
Determine a distância até o centroide da área da seção transversal da viga; depois, determine o momento de inércia em relação ao eixo .
Passo 1
E aí! tudo certo?
Nesse problema foi dada uma seção transversal de uma viga e nosso objetivo é calcular seu centroide e o momento de inércia em relação ao eixo .
Tem ideia de como fazemos isso?
Para resolver esse problema podemos aplicar a fórmulinha do somatório:
E para encontrar o momento de inércia da área podemos usar o teorema dos eixos paralelos.
Bora começar!
Passo 2
Primeiro vamos calcular a componente do centroide da área...
No passo 1 vimos que:
Então, separando em áreas primitivas, temos que:
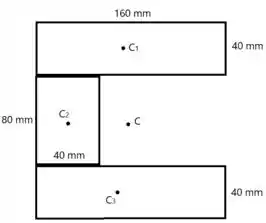
Usando como referência o canto inferior esquerdo da temos que:

Substituindo na fórmula do centroide...
Tranquilo até aqui?
Passo 3
Agora vamos aplicar o teorema dos eixos paralelos para calcular o momento de inércia de região.
Para facilitar, vamos escrever em forma de tabela...
Lembrando que o momento de inercia do centroide de um retângulo é:

Substituindo na fórmula de , temos:
E aí! entendeu tudo? Responde Aí!