Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 7

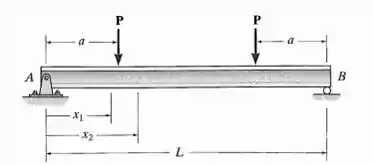
Determine as equações da linha elástica para a viga utilizando as coordenadas x1 e x2. Especifique a inclinação em A e o deslocamento no centro do eixo. EI é constante.

Passo 1

Faaaaala aí! O que ele quer aqui é que a gente use dois sistemas de referência diferentes para achar v x , a equação da linha elástica. Os dois com origem na ponta esquerda da viga: ( x 1 ) e ( x 2 ).

Aí a gente usa que

E I d 2 v d x 2 = M x

Acha o momento, integra duas vezes e acha v x para esses dois casos.

Antes de tudo, a gente só precisa especificar as reações dessa viga. Por simetria, vemos que

F A = F B = P

E repara que só temos três seções para examinar. Do apoio A   até o primeiro P . Entre as forças P , e do segundo P até o apoio B .

Agora sim. Bora!

Passo 2

Vamos achar a função momento para o intervalo 0 ≤ x 1 ≤ a :

Repara que é mais fácil achar o momento nesse intervalo olhando só para parte esquerda da viga, ao cortar ela numa seção dentro do nosso intervalo, e esquecendo a direita. Então ajuda se a gente usar o sistema x 1 , beleza?

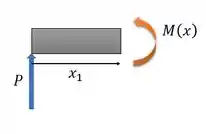
O momento M x fica:

M x 1 = P x 1

Sabemos que:

E I d 2 v 1 d x 1 ² = M x

Logo:

E I d 2 v 1 d x 1 2 = P x 1

Integrando duas vezes:

E I d v 1 d x 1 = P 2 x 1 2 +   C 1

E I v 1 = P 6 x 1 3 + C 1 x 1 + C 2

Passo 3

Aí como o enunciado pediu para usar os dois, para a outra parte da viga, usamos x 2 .

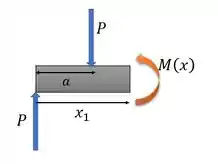
Será o mesmo processo aqui, só que para a ≤ x 2 ≤ L - a :

M x 2 = P x 1 - P x 1 - a

M x 2 = P a

Logo:

E I d 2 v 2 d x 2 2 = P a

Integrando duas vezes:

E I d v 2 d x 2 = P a x 2 + C 3

E I v 2 = P a 2 x 2 2 + C 3 x 2 + C 4

Aí cê pode pensar: mas e equação para a terceira seção? Não vamos achar? Cara, não precisa, porque nossa viga é simétrica e o carregamento também. Então, a deflexão que ocorre na primeira seção, ocorre como um espelho na terceira seção. Tranquilo? Vamos seguir!

Passo 4

Agora, vamos aplicar as condições de contorno e continuidade para achar as constantes.

A primeira condição é

x 1 = 0 → v 1 = 0

Isso mostra que no apoio a deflexão é zero. Substituindo na nossa equação de v 1 :

E I v 1 = P 6 x 1 3 + C 1 x 1 + C 2

0 = 0 + C 2

C 2 = 0

Passo 5

E outras consições que a gente tem são

x 1 = x 2 = a → v 1 = v 2

x 1 = a   e   x 2 = L - a → v 1 = v 2

Esses representam a simetria e continuidade da viga nos pontos onde temos cargas concentradas P .

Neles, a deflexão é igual. O ponto logo antes do primeiro P (em v 1 ), o ponto logo depois do primeiro P (em v 2 ) e o ponto logo antes do segundo P (em v 2 ), todos tem a mesma deflexão.

Então a gente pode usar:

v 1 = v 2

Substituindo as expressões e simplificando:

P 6 x 1 3 + C 1 x 1 + C 2 = P a 2 x 2 2 + C 3 x 2 + C 4

Temos que isso vale para x 1 = x 2 = a :

P 6 a 3 + C 1 a = P a 3 2 + C 3 a + C 4     i

E para x 1 = a e x 2 = L - a :

P 6 a 3 + C 1 a = P a 2 L - a 2 + C 3 L - a 2 + C 4   i i

Passo 6

E podemos usar também que

x 1 = x 2 = a → E I d v 1 d x 1 = E I d v 2 d x 2

Porque a derivada de v x também deve ser continua onde temos força concentrada. Substituindo as expressões e x 1 = x 2 = a :

P 2 x 1 2 +   C 1 = P a x 2 + C 3

P 2 a 2 +   C 1 = P a 2 + C 3   i i i

As equações i ,   i i ,   i i i formam um sisteminha para achar as outras constantes. Resolvendo ele, vamos achar:

C 1 = P a 2 a - L ; C 2 = 0 ; C 3 = - P a L 2 ; C 4 = - P a 3 6

Passo 7

Agora é pegar as constantes e substituir nas equações para achar v x . A de x 1 fica:

E I v 1 = P 6 x 1 3 + C 1 x 1 + C 2

v 1 = P x 1 6 E I x 1 2 + 3 a a - L

E a de x 2 :

E I v 2 = P a 2 x 2 2 + C 3 x 2 + C 4

v 2 = P a 6 E I 3 x 2 x 2 - L + a 2

Passo 8

A inclinação em A ocorre em x 1 = 0 , e será dada pela derivada de v 1 nesse ponto:

v 1 = P 6 E I x 1 3 + 3 a x 1 a - L

v 1 ' = P 6 E I 3 x 1 2 + 3 a a - L

Logo

θ A = P 6 E I 3 a a - L

θ A = P a a - L 2 E I

O deslocamento no centro será dado por x 2 = L 2 em v 2 :

v 2 = P a 6 E I 3 x 2 x 2 - L + a 2

v 2 = P a 6 E I 3 L 2 L 2 - L + a 2

v m á x = P a 2 4 E I 4 a 2 - 3 L 2

Resposta

v 1 = P x 1 6 E I x 1 2 + 3 a a - L

v 2 = P a 6 E I 3 x 2 x 2 - L + a 2

θ A = P a a - L 2 E I

v m á x = P a 2 4 E I 4 a 2 - 3 L 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que a tensão admissível para ao aço é de 160M P a , selecione a viga de perfil I mais econômica para suportar o carregamento mostrado.
As vigas A B , B C e C D têm a seção transversal mostrada na figura e são unidas por pino em B e C . Sabendo que a tensão normal admissível é de + 110M P a em tração e de - 150M P a em compressão, det
Determine o maior valor possível de P para a viga e o carregamento mostrados, sabendo que a tensão normal admissível é de + 8M P a em tração e - 18M P a em compressão.
Considerando que a reação ascendente do solo seja uniformemente distribuída e sabendo que a tensão normal admissível para o aço utilizado é de 165M P a , selecione a viga de mesa larga mais econômica
Determine o maior valor admissível de carga distribuída w para a viga mostrada, sabendo que a tensão normal admissível é de + 80M P a em tração e de - 130M P a de compressão.