Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.3 - Ex. 16
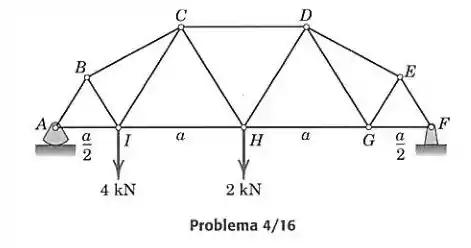
Determine as forças nos elementos , e da treliça carregada. Todos os ângulos são , e .
Passo 1
Primeiro devemos calcular as forças externas aplicadas na treliça em e . O apoio em gera apenas reação para cima.
Agora calculando o momento em torno de achamos :
E substituímos para achar
Passo 2
Agora devemos resolver as equações de equilíbrio em e para cada nó. As forças positivas indicam tração e as negativas compressão, e sempre trataremos as forças desconhecidas como tração.
Nó A:
Passo 3
Nó B:
Podemos ver que e então está inclinado com a horizontal.
Passo 4
Nó I:
Resposta
Exercícios de Livros Relacionados
6.49. Uma treliça de telhado de uma água é carregada tal como mostra a figura. Determine a força nos elementos CF, DE e DF.
6.50. Uma treliça de telhado de uma água é carregada tal como mostra a figura. Determine a força nos elementos EG, GH e HJ.
6.53. Uma treliça de telhado Pratt é carregada tal como mostra a figura. Determine a força nos elementos CE, DE e DF.
6.54. Uma treliça de telhado Pratt é carregada tal como mostra a figura. Determine a força nos elementos FH, FI e GI.
Determine a força em cada elemento da treliça mostrada na figura.